Kooperation: R. H. W. Hoppe (Universität Augsburg), H. Yserentant (Universität Tübingen), R. Beck, B. Erdmann, R. Roitzsch (ZIB)
Beschreibung der Forschungsarbeit:
Das Projekt ist die Fortsetzung eines entsprechenden Vorhabens im Berichtsjahr 1994.
Monotone Mehrgittermethoden stellen eine Erweiterung klassischer Verfahren für selbstadjungierte elliptische Probleme auf gewisse stückweise lineare Energiefunktionale dar. Die Grundidee besteht in einer Beschränkung der Grobgitterkorrektur auf die Umgebung der aktuellen geglätteten Iterierten, in der eine Linearisierung des Energiefunktionals möglich ist. Auf diese Weise erhält man ein global konvergentes Verfahren, mit dem sich Hindernisprobleme oder zeitdiskrete Probleme vom Stefan-Typ mit vergleichbarer Effizienz lösen lassen wie im entsprechenden linearen Fall.
Natürlich sollte die zugrundeliegende Folge von Gittern an die Lösung des jeweiligen Problems angepaßt sein. Ein a posteriori Fehlerschätzer, der aus einer Zerlegung des Defektproblems in lokale Teilprobleme besteht, liefert lokale Fehlerindikatoren, welche ihrerseits die adaptive Verfeinerung der Gitter steuern.
Das gesamte Verfahren wurde in [1] ausführlich dargestellt. Eine entsprechende Monographie ist in Arbeit. Einige Bemerkungen zu den Effektivitätsraten des Fehlerschätzers finden sich in [2], während [3] eine algorithmisch motivierte Darstellung enthält.
Der Zugang ist unabhängig von der
Raumdimension. Im Rahmen des Projekts ,,KASKADE --- eine Toolbox für
adaptive Multilevelmethoden``
(siehe S. 
)
erfolgte die Implementierung des 3D-Falls.
Numerische Experimente zeigen sogar eine quantitative
Übereinstimmung mit entsprechenden
Resultaten in zwei Raumdimensionen.
Die Ergebnisse für ein Modellproblem mit dem in Abbildung 1
dargestellten freien Rand befinden sich in Tabelle 1.
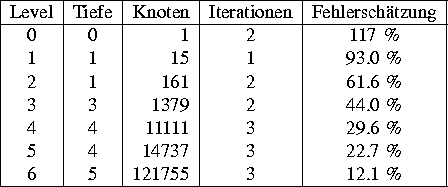
Tabelle 1: Approximationsgeschichte
Die Anwendung und Erweiterung monotoner Mehrgittermethoden
auf Kontaktprobleme ist Gegenstand eines eigenen Projekts
(siehe S. ). Weitere Entwicklungen
im Rahmen einer Zusammenarbeit mit O. Klein
(siehe S. ) und D. Hömberg (siehe S. )
aus der Forschungsgruppe 1 sind geplant.
Projektliteratur:
