



Next: Adaptive monotone Mehrgittermethoden
Up:
Previous: Numerische Lösung schwach
Bearbeiter: H. Sandmann
Kooperation: U. Nowak (ZIB)
Beschreibung der Forschungsarbeit:
Bei der numerischen Lösung von Anfangswertaufgaben
für Systeme nichtlinearer Algebro-Differentialgleichungen, z. B. aus der
chemischen Prozeßsimulation und Verfahrenstechnik,
sind große schwach besetzte nichtlineare Gleichungssysteme 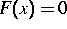 mit irregulär strukturierter Jacobi-Matrix zu lösen, um
konsistente Anfangswerte zu gewinnen.
Auch während der dynamischen Simulation bei
Reinitialisierung des Prozesses an einer Unstetigkeitsstelle und
schließlich bei der Bestimmung
stationärer Werte sind Lösungen nichtlinearer Gleichungssyteme
zu berechnen.
Die Modellierung der verkoppelten Teile realer Anlagen und/oder
Prozeßabläufe
prägt F und der zugehörigen Jacobi-Matrix eine schwache Besetztheit und
Teilsystem-Struktur ein.
Außer diesen Struktureigenschaften sind für die Unbekannten restriktive
Wertebereiche gegeben, wie positive Konzentrationen, Dichten u. a. m.
Die durch die Strukturierung gegebene grob- und fein-granulare Parallelität
der Aufgabe wurde bei einer Implementierung eines skalierbaren synchronen
Algorithmus auf CRAY T3D berücksichtigt.
mit irregulär strukturierter Jacobi-Matrix zu lösen, um
konsistente Anfangswerte zu gewinnen.
Auch während der dynamischen Simulation bei
Reinitialisierung des Prozesses an einer Unstetigkeitsstelle und
schließlich bei der Bestimmung
stationärer Werte sind Lösungen nichtlinearer Gleichungssyteme
zu berechnen.
Die Modellierung der verkoppelten Teile realer Anlagen und/oder
Prozeßabläufe
prägt F und der zugehörigen Jacobi-Matrix eine schwache Besetztheit und
Teilsystem-Struktur ein.
Außer diesen Struktureigenschaften sind für die Unbekannten restriktive
Wertebereiche gegeben, wie positive Konzentrationen, Dichten u. a. m.
Die durch die Strukturierung gegebene grob- und fein-granulare Parallelität
der Aufgabe wurde bei einer Implementierung eines skalierbaren synchronen
Algorithmus auf CRAY T3D berücksichtigt.
Das Lösungsverfahren kann zwar von einem
zulässigen 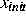 ausgehen, aber
auch ein affin invariantes Newton-Verfahren muß von
ausgehen, aber
auch ein affin invariantes Newton-Verfahren muß von 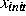 aus
nicht notwendig konvergieren.
aus
nicht notwendig konvergieren.
In diesem Fall müssen
in einem ersten Schritt mit einem Suchverfahren Startwerte für ein
modifiziertes Newton-Verfahren ermittelt werden.
Hierbei werden sukzessiv die aufgrund der Modellierung stets
unterbestimmten nichtlinearen Teilsysteme 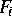 linearisiert.
Die unterbestimmten linearen Gleichungssysteme werden unter Verwendung von
Moore-Penrose-Pseudo-Inversen gelöst. Aus diesem Prozeß erhält man
zulässige Werte für die in F linear gekoppelten Unbekannten und
grobe Näherungen für die übrigen.
Mit dieser Näherung wird mittels
Block-Gauß-Seidel-Newton-Iterationsverfahren (jeder Block entspricht
einem Teilsystem
linearisiert.
Die unterbestimmten linearen Gleichungssysteme werden unter Verwendung von
Moore-Penrose-Pseudo-Inversen gelöst. Aus diesem Prozeß erhält man
zulässige Werte für die in F linear gekoppelten Unbekannten und
grobe Näherungen für die übrigen.
Mit dieser Näherung wird mittels
Block-Gauß-Seidel-Newton-Iterationsverfahren (jeder Block entspricht
einem Teilsystem 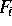 ) eine neue Näherungslösung für F = 0 bestimmt.
Die Newton-Iteration für
) eine neue Näherungslösung für F = 0 bestimmt.
Die Newton-Iteration für 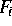 wird mit der aus
wird mit der aus 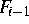 gewonnenen Näherung gestartet und
die Newton-Korrektur unter Verwendung von Pseudo-Inversen berechnet.
Die Näherungslösung aus dem
Block-Gauß-Seidel-Newton-Iterationsverfahren
dient nun als Startwert für ein modifiziertes gedämpftes
Newton-Verfahren für F = 0.
gewonnenen Näherung gestartet und
die Newton-Korrektur unter Verwendung von Pseudo-Inversen berechnet.
Die Näherungslösung aus dem
Block-Gauß-Seidel-Newton-Iterationsverfahren
dient nun als Startwert für ein modifiziertes gedämpftes
Newton-Verfahren für F = 0.
Der Lösungsprozeß wird durch den Umstand kompliziert,
daß numerisch singuläre Jacobi-Matrizen
nicht auszuschließen sind. Deshalb wurde das Newton-Verfahren mit einer
Matrix-Analyse ausgestattet, die vor allem
die schwache Besetztheit und
teilsystemorientierte Strukturierung von F und der Jacobi-Matrix
ausnutzt.
Durch Ändern weniger Näherungslösungskomponenten, die die
Singularität bewirken, läßt sich
eine reguläre Jacobi-Matrix erhalten, wobei die schwache Besetztheit
eine wesentliche Vorausssetzung ist, da sonst die durch Änderung
gewisser Lösungskomponenten erzeugte neue Aufgabe der alten nicht mehr
benachbart ist.




Next: Adaptive monotone Mehrgittermethoden
Up:
Previous: Numerische Lösung schwach
Group_of_Office
Mon May 13 20:25:53 MET DST 1996
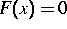 mit irregulär strukturierter Jacobi-Matrix zu lösen, um
konsistente Anfangswerte zu gewinnen.
Auch während der dynamischen Simulation bei
Reinitialisierung des Prozesses an einer Unstetigkeitsstelle und
schließlich bei der Bestimmung
stationärer Werte sind Lösungen nichtlinearer Gleichungssyteme
zu berechnen.
Die Modellierung der verkoppelten Teile realer Anlagen und/oder
Prozeßabläufe
prägt F und der zugehörigen Jacobi-Matrix eine schwache Besetztheit und
Teilsystem-Struktur ein.
Außer diesen Struktureigenschaften sind für die Unbekannten restriktive
Wertebereiche gegeben, wie positive Konzentrationen, Dichten u. a. m.
Die durch die Strukturierung gegebene grob- und fein-granulare Parallelität
der Aufgabe wurde bei einer Implementierung eines skalierbaren synchronen
Algorithmus auf CRAY T3D berücksichtigt.
mit irregulär strukturierter Jacobi-Matrix zu lösen, um
konsistente Anfangswerte zu gewinnen.
Auch während der dynamischen Simulation bei
Reinitialisierung des Prozesses an einer Unstetigkeitsstelle und
schließlich bei der Bestimmung
stationärer Werte sind Lösungen nichtlinearer Gleichungssyteme
zu berechnen.
Die Modellierung der verkoppelten Teile realer Anlagen und/oder
Prozeßabläufe
prägt F und der zugehörigen Jacobi-Matrix eine schwache Besetztheit und
Teilsystem-Struktur ein.
Außer diesen Struktureigenschaften sind für die Unbekannten restriktive
Wertebereiche gegeben, wie positive Konzentrationen, Dichten u. a. m.
Die durch die Strukturierung gegebene grob- und fein-granulare Parallelität
der Aufgabe wurde bei einer Implementierung eines skalierbaren synchronen
Algorithmus auf CRAY T3D berücksichtigt.



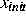 ausgehen, aber
auch ein affin invariantes Newton-Verfahren muß von
ausgehen, aber
auch ein affin invariantes Newton-Verfahren muß von 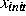 aus
nicht notwendig konvergieren.
aus
nicht notwendig konvergieren.
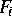 linearisiert.
Die unterbestimmten linearen Gleichungssysteme werden unter Verwendung von
Moore-Penrose-Pseudo-Inversen gelöst. Aus diesem Prozeß erhält man
zulässige Werte für die in F linear gekoppelten Unbekannten und
grobe Näherungen für die übrigen.
Mit dieser Näherung wird mittels
Block-Gauß-Seidel-Newton-Iterationsverfahren (jeder Block entspricht
einem Teilsystem
linearisiert.
Die unterbestimmten linearen Gleichungssysteme werden unter Verwendung von
Moore-Penrose-Pseudo-Inversen gelöst. Aus diesem Prozeß erhält man
zulässige Werte für die in F linear gekoppelten Unbekannten und
grobe Näherungen für die übrigen.
Mit dieser Näherung wird mittels
Block-Gauß-Seidel-Newton-Iterationsverfahren (jeder Block entspricht
einem Teilsystem 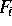 ) eine neue Näherungslösung für F = 0 bestimmt.
Die Newton-Iteration für
) eine neue Näherungslösung für F = 0 bestimmt.
Die Newton-Iteration für 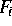 wird mit der aus
wird mit der aus 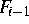 gewonnenen Näherung gestartet und
die Newton-Korrektur unter Verwendung von Pseudo-Inversen berechnet.
Die Näherungslösung aus dem
Block-Gauß-Seidel-Newton-Iterationsverfahren
dient nun als Startwert für ein modifiziertes gedämpftes
Newton-Verfahren für F = 0.
gewonnenen Näherung gestartet und
die Newton-Korrektur unter Verwendung von Pseudo-Inversen berechnet.
Die Näherungslösung aus dem
Block-Gauß-Seidel-Newton-Iterationsverfahren
dient nun als Startwert für ein modifiziertes gedämpftes
Newton-Verfahren für F = 0.