Bearbeiter: O. Klein
Förderung: EU, HCM-Netzwerk ,,Phase Transitions and Surface Tension``
Beschreibung der Forschungsarbeit:
In diesem Projekt werden verschiedene Modelle für den Phasenübergang fest--flüssig betrachtet; insbesondere wird untersucht, wie man mit Hilfe von Näherungslösungen der Penrose-Fife Phasenfeldgleichungen Approximationslösungen für das Stefan-Problem gewinnen kann.
Das Stefan-Problem ist ein Ansatz zur Modellierung des fest--flüssig Phasenübergangs. In der Enthalpie--Formulierung des Stefan-Problems wird verlangt, daß
im distributionellen Sinne gilt und daß fast überall
ist.
Dabei ist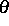 
die absolute Temperatur,
q der Wärmefluß
und 
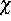ein Ordnungsparameter, der in der festen
Phase 0 und in der flüssigen Phase 1 ist.
Die gegebene Funktion g repräsentiert Wärmequellen oder -senken,
H ist der Heaviside-Graph, und
die Schmelztemperatur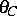 
ist, ebenso wie
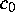und L, eine positive Materialkonstante.
Penrose und Fife verwenden
in [6] zur
Modellierung von diffusionsgesteuerten Phasenübergängen
einen Landau-Ginzburg-Ansatz für die freie Energie.
Die sich dabei ergebenden
Phasenfeldgleichungen lauten
für einen nicht konservierten Ordnungsparameter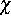 
in einem Spezialfall
Dabei
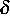sind 
und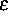 
positive Konstanten, und
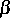ist der inverse
Heaviside-Graph, d. h.
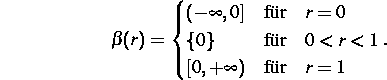
Betrachtet man dieses System genauer, so stellt man fest, daß es
für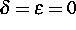 
äquivalent zur Enthalphie-Formulierung
des Stefan-Problems
(1)--(2)
ist.
Colli und Sprekels untersuchen in [3,4]
für einen
Wärmefluß, der sich als Gradient der inversen Temperatur ergibt,
d. h.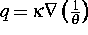 
für eine positive
Materialkonstante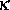 
, wie sich die
Lösungen
der Penrose-Fife Phasenfeldgleichungen
(3)--(4)
verhalten, wenn
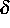und 
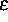gegen 0 gehen.
Sie können zeigen, daß diese Lösungen gegen eine
Lösung des Stefan-Problems
(1)--(2)
konvergieren, wenn man
geeignete Rand- und Anfangsbedingungen betrachtet.
Weiterhin zeigten Colli und Sprekels, daß man, wenn
nur einer der Parameter
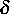und 
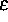gegen 0 geht,
Konvergenz gegen die sogenannten relaxierten Stefan-Probleme erhält, wie
sie z. B. (siehe [7]) zur Modellierung des Erstarrens mit der
Berücksichtigung von Unterkühlung verwendet werden.
In diesem Projekt soll nun ein numerisches Verfahren zur Lösung des Stefan-Problems entwickelt werden, welches auf diesem Grenzübergang beruht. Weil die Lösungen der Penrose-Fife Gleichungen glatter sind als die Lösung des Stefan-Problems, hofft man so bessere numerische Resultate zu erzielen, als bei einer direkten Diskretisierung des Stefan-Problems.
Im Berichtszeitraum wurde (siehe {[5]) für die
Penrose-Fife Phasenfeldgleichungen
(3)--(4)
ein Schema zur Semidiskretisierung in der Zeit formuliert, welches in
drei Raumdimensionen konvergent ist.
Außerdem wurde gezeigt, daß analoge Konvergenzaussagen zu
denen in Colli-Sprekels [4] gelten, wenn man neben der
Zeitschrittweite h auch noch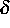 
und/oder 
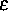gegen
0 gehen läßt.
Unter Verwendung von Techniken aus [1]
wurden Fehlerabschätzungen durchgeführt, die zeigen, daß
der Fehler durch die zeitliche Diskretisierung von der Ordnung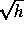 
ist.
Die Fehlerabschätzungen für das Schema liefern Abschätzungen
für die Konvergenzrate der Lösungen der nicht diskreten Penrose-Fife
Phasenfeldgleichungen gegen die Lösung des Stefan-Problems.
Im nächsten Jahr soll untersucht werden, ob und unter welchen Voraussetzungen man beweisen kann, daß der zeitliche Diskretisierungsfehler von der Ordnung h ist. Dabei sollen auch Techniken aus [2] verwendet werden.
Hauptziel der Arbeit im nächsten Jahr ist es, aufbauend auf der Semidiskretisierung in Zusammenarbeit mit der Forschungsgruppe 3 ein numerisches Verfahren zu entwickeln und zu implementieren. Mit diesem sollen zunächst die Penrose-Fife Phasenfeldgleichungen und später das Stefan-Problem und die relaxierten Stefan-Probleme näherungsweise gelöst werden. Dabei soll mit Orginaldaten gerechnet werden, um realistisches Materialverhalten zu simulieren.
Projektliteratur:
,
WIAS-Preprint No. 199, Berlin 1995,
erscheint 1997 in Adv. Math. Sci. Appls.
