



Bearbeiter: U. Krause
Förderung: DFG, SFB 256
Kooperation: J. Frehse, Sonderforschungsbereich 256 ,,Nichtlineare partielle Differentialgleichungen`` der Rheinischen Friedrich-Wilhelms-Universität Bonn;
K. Gärtner, Institut für Integrierte Systeme, Eidgenössische Technische Hochschule Zürich
Beschreibung der Forschungsarbeit:
Die fortdauernde Miniaturisierung in der Mikroelektronik [1] erhöht die Abhängigkeit der Funktion der Bauelemente von Quanteneffekten wesentlich und erfordert sowohl den Versuch der ständigen Anpassung bewährter Modelle als auch die Suche nach neuen, handhabbaren Gleichungen.
Halbleitergleichungen mit der Einteilchenenergie als einer unabhängigen Variablen [2] entstehen, wenn man in der quasiklassischen Boltzmanngleichung die Verteilungsfunktion und die Streuraten auf geeignete Weise über die Isoenergieflächen der elektronischen Bandstruktur mittelt. Auf diese Weise hat man die für die Funktion eines Bauelementes in einem Regime fern vom thermodynamischen Gleichgewicht der Ladungsträger wesentliche Größe der Einteilchenenergie E explizit als Variable in den Gleichungen. Im einfachsten Fall eines räumlich eindimensionalen Gebietes lauten sie
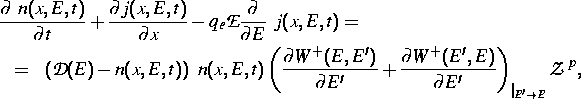
wobei der Strom j durch
mit

gegeben ist. Die Poisson-Gleichung lautet
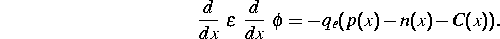
Dabei sind
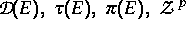 und
und 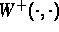 gegebene,
das Halbleitermaterial charakterisierende Größen,
gegebene,
das Halbleitermaterial charakterisierende Größen, 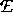 ist die
elektrische Feldstärke,
ist die
elektrische Feldstärke, 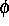 das elektrostatische Potential,
das elektrostatische Potential, 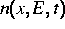 die Elektronendichte und
die Elektronendichte und 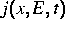 die Stromdichte der Elektronen.
die Stromdichte der Elektronen.
Die Variable E gestattet die direkte Modellierung von Zuständen des Bauelementes und wirft andererseits neue Probleme auf: Wegen der verbotenen Zone eines Halbleiters ist das Gebiet, in dem man die Gleichungen zu betrachten hat, nicht zusammenhängend. Aus physikalischen Gründen dürfen an den Bandkanten keine Randbedingungen gefordert werden. In jeder Formulierung der Gleichungen treten Streuraten W zwischen verschiedenen Energiezuständen der Ladungsträger auf. Die gegenwärtigen Untersuchungen des Modells befassen sich mit der Dynamik der Elektronen und Löcher in diesem Modell:
Projektliteratur:



