Kooperation: M. Hillmann (INPRO GmbH Berlin), G. Zumbusch (ZIB)
Beschreibung der Forschungsarbeit:
Das Projekt wurde im April 1995 ins Leben gerufen mit dem Ziel der
Weiterentwicklung von adaptiven monotonen Mehrgittermethoden für freie
Randwertaufgaben (siehe Jahresbericht 1994 und S. 
)
auf Probleme der nichtlinearen Mechanik.
Wir betrachten das quasistatische, elastomechanische Problem des Auftreffens
eines Körpers 
auf ein absolut starres und festes Hindernis unter
Berücksichtigung dabei auftretender trockener Reibung am Kontaktrand 
.
Ausgehend von den Laméschen Gleichungen für die Verschiebung u der Massepunkte
von 
erhalten wir durch die zusätzlichen Bedingungen an die Verschiebung
und die Spannung 
am zunächst unbekannten Kontaktrand eine
nichtlineare Randwertaufgabe.
Als Kontaktbedingungen dienen uns die sogenannten Signorini-Bedingungen,
welche besagen, daß der Körper 
zu keiner Zeit in das Hindernis eindringen
kann und daß am Kontaktrand erst dann eine Spannung in Normalenrichtung auftreten
kann, wenn es zum Kontakt gekommen ist.
Diese ist dann in das Innere des Körpers gerichtet.
Hinzu kommen die als Coulombsches Gesetz bekannten Reibungsbedingungen.
Man geht hierbei solange von Haftreibung aus, bis am Kontaktrand der Wert der
Tangentialspannung betragsmäßig das Produkt aus Reibungskoeffizienten und
Normalspannung erreicht hat.
Nun gleitet der Körper entlang der Oberfläche des Hindernisses.
Die Geschwindigkeit seiner Massepunkte am Kontaktrand in Tangentialrichtung
ist negativ proportional zur Tangentialspannung (siehe Abbildung 1).
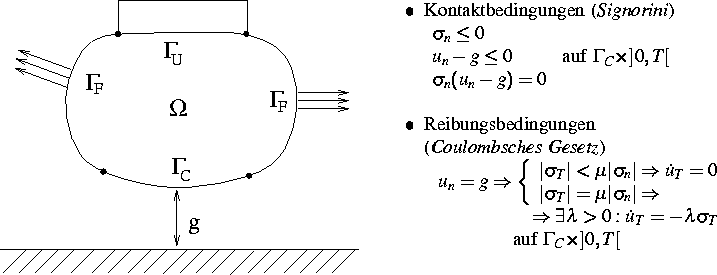
Abb. 1:
Beim elastomechanischem Auftreffen des Körpers 
auf ein starres Hindernis
betrachten wir zusätzliche Kontakt- und Reibungsbedingungen.
Beim Übergang zur Variationsformulierung wird aus der klassischen Formulierung eine Quasi-Variationsungleichung. Existenz-- und Eindeutigkeitsnachweise sind Gegenstand aktueller Forschung. Für eine numerische Lösung des Minimierungsproblems sind Newtonverfahren wegen nichtdifferenzierbarer Anteile im Energiefunktional nicht möglich, statt dessen verwendet man üblicherweise penalty-Verfahren. Diese haben jedoch den Nachteil, daß die Kondition des zugehörigen diskreten Problems vom zusätzlich eingeführten Strafterm abhängt. Ziel ist es daher, das Minimierungsproblem direkt mit Hilfe adaptiver monotoner Mehrgittermethoden zu lösen.
Als Grundlage für unsere numerischen Experimente wird uns das Programmpaket
KASKADE dienen, welches auf diese Problemklasse hin erweitert werden soll.
Eine Zusammenarbeit mit dem ZIB und den Mitarbeitern des
Projektes ,,KASKADE --- eine Toolbox für adaptive Multilevelmethoden``
(siehe S. ) besteht.
Erste Ergebnisse für Probleme in zunächst zwei Raumdimensionen werden für
das erste Halbjahr 1996 erwartet.