



Next: Fluidtransport in porösen
Up:
Previous: Kontakt mit Reibung
Bearbeiter:
J. Fuhrmann
Kooperation: A. Reusken (TU Eindhoven),
K. Gärtner (ETH Zürich),
N. Neuss (Universität Heidelberg),
G. Wittum (Universität Stuttgart)
Förderung: DFG (SFB 359)
Beschreibung der Forschungsarbeit:
Die Konstruktion
robuster Multigrid- und Multilevelverfahren bereitet Schwierigkeiten
z. B. für
Konvektions-Diffusionsprobleme,
wie sie bei der Lösung der Halbleitergleichungen oder
der Simulation von Transportprozessen in porösen Medien (S.  ) auftreten,
und für diskrete Probleme auf unstrukturierten
Netzen, denen keine Finite-Elemente-Hierarchie zugrundeliegt.
Algebraische Mehrgitterverfahren,
deren Grundidee darin besteht, die
notwendigen
Grobgitterprobleme und Transferoperatoren allein aus der auf dem
feinen Gitter vorhandenen Information zu erzeugen,
lassen auf eine Lösung dieser Fragestellung hoffen.
) auftreten,
und für diskrete Probleme auf unstrukturierten
Netzen, denen keine Finite-Elemente-Hierarchie zugrundeliegt.
Algebraische Mehrgitterverfahren,
deren Grundidee darin besteht, die
notwendigen
Grobgitterprobleme und Transferoperatoren allein aus der auf dem
feinen Gitter vorhandenen Information zu erzeugen,
lassen auf eine Lösung dieser Fragestellung hoffen.
Ein Schritt eines Zweigitterverfahrens zur Lösung des Problems Au=f besteht
aus folgenden Komponenten:
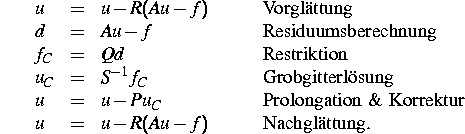
Die rekursive Anwendung dieses Verfahrens führt zum Mehrgitterverfahren.
Die Idee des in diesem Projekt bearbeiteten modularen
algebraischen Mehrgitterverfahrens
besteht in der Herleitung der Komponenten
aus der Matrixpartitionierung
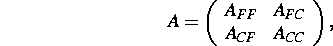
welche durch die -- unter Umständen a priori gegebene -- Einteilung der Variablen in Grobgitter- und Feingittervariablen
erzeugt wird.
Seien L und U invertierbar und 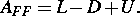 Wir definieren dann:
Wir definieren dann:
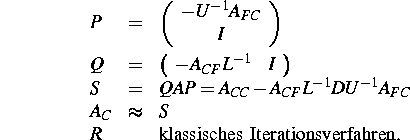
Für 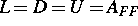 und
und 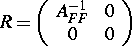 erhalten wir einen exakten Löser. Die Invertierung von
erhalten wir einen exakten Löser. Die Invertierung von 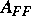 ist aber nur
in Spezialfällen möglich.
Sind
ist aber nur
in Spezialfällen möglich.
Sind 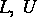 untere bzw. obere Dreiecksmatrizen, erhalten wir eine Art
Gauß-Seidel-Schritt zur Invertierung von
untere bzw. obere Dreiecksmatrizen, erhalten wir eine Art
Gauß-Seidel-Schritt zur Invertierung von 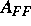 und damit einen
Vorkonditionierer für ein iteratives Lösungsverfahren.
und damit einen
Vorkonditionierer für ein iteratives Lösungsverfahren.
Die Definition der Grobgitterknoten kann Informationen aus verschiedenen Quellen
benutzen. Auf logisch orthogonalen Netzen wird die übliche Vergröberung
verwendet. Auf hierarchisch strukturierten Netzen kann die dort gegebene
Strukturinformation ausgewertet werden.
Zum Beispiel ist es bereits möglich, die
hierarchische Struktur der durch KASKADE (S.  )
erzeugten Netze auszunutzen und
einen effektiven Vorkonditionierer für Diffusionsprobleme mit Koeffizientensprüngen,
die durch die Gitterverfeinerung nicht erfaßt sind, zu definieren.
)
erzeugten Netze auszunutzen und
einen effektiven Vorkonditionierer für Diffusionsprobleme mit Koeffizientensprüngen,
die durch die Gitterverfeinerung nicht erfaßt sind, zu definieren.
Um auf allgemeinen unstrukturierten Netzen arbeiten zu können, muß die Wahl
der Grobgitterknoten untersucht werden.
Insbesondere für Konvektions-Diffusionsprobleme ist der Vergleich mit den
Verfahren von A. Reusken geplant, deren Struktur sehr ähnlich ist.
Projektliteratur:
- J. FUHRMANN, A modular algebraic multilevel method,
WIAS-Preprint No. 203, Berlin 1995.





Next: Fluidtransport in porösen
Up:
Previous: Kontakt mit Reibung
Group_of_Office
Mon May 13 20:25:53 MET DST 1996
 ) auftreten,
und für diskrete Probleme auf unstrukturierten
Netzen, denen keine Finite-Elemente-Hierarchie zugrundeliegt.
Algebraische Mehrgitterverfahren,
deren Grundidee darin besteht, die
notwendigen
Grobgitterprobleme und Transferoperatoren allein aus der auf dem
feinen Gitter vorhandenen Information zu erzeugen,
lassen auf eine Lösung dieser Fragestellung hoffen.
) auftreten,
und für diskrete Probleme auf unstrukturierten
Netzen, denen keine Finite-Elemente-Hierarchie zugrundeliegt.
Algebraische Mehrgitterverfahren,
deren Grundidee darin besteht, die
notwendigen
Grobgitterprobleme und Transferoperatoren allein aus der auf dem
feinen Gitter vorhandenen Information zu erzeugen,
lassen auf eine Lösung dieser Fragestellung hoffen. 



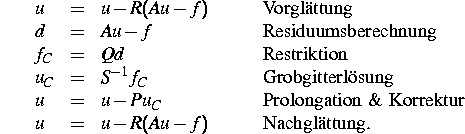
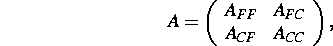
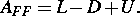 Wir definieren dann:
Wir definieren dann:
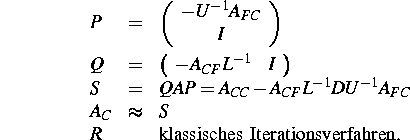
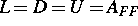 und
und 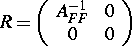 erhalten wir einen exakten Löser. Die Invertierung von
erhalten wir einen exakten Löser. Die Invertierung von 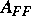 ist aber nur
in Spezialfällen möglich.
Sind
ist aber nur
in Spezialfällen möglich.
Sind 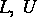 untere bzw. obere Dreiecksmatrizen, erhalten wir eine Art
Gauß-Seidel-Schritt zur Invertierung von
untere bzw. obere Dreiecksmatrizen, erhalten wir eine Art
Gauß-Seidel-Schritt zur Invertierung von 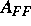 und damit einen
Vorkonditionierer für ein iteratives Lösungsverfahren.
und damit einen
Vorkonditionierer für ein iteratives Lösungsverfahren. 
