Kooperation: P. Knabner (Universität Erlangen-Nürnberg), A. Erber (Erdöl-Erdgas Gommern GmbH)
Förderung: DFG (SFB 359)
Beschreibung der Forschungsarbeit:
In Fortsetzung des gleichgelagerten Projektes aus dem Jahre 1994 wurde
der auf der
Verwendung einer impliziten Zeitdiskretisierung und
eines Newton-Verfahrens
zur Auflösung der Nichtlinearität
in Verbindung mit einem mehrgittervorkonditionierten
BICGstab-Verfahren
(S. 
) für die linearen Probleme
basierende zeitlich adaptive numerische Algorithmus
zur Lösung nichtlinerarer Diffusionsprobleme
vervollkommnet.
Im Rahmen des KASKADE-Projektes
(S. )
wurden die technischen Voraussetzungen
für die Entwicklung räumlich adaptiver Verfahren geschaffen.
Der Algorithmus wurde auf degenerierte parabolische Probleme, wie z. B. die Poröse-Medien-Gleichung
erweitert. Es wurden numerische Experimente durchgeführt, die zeigen, daß die auf diese Weise erhältlichen numerischen Lösungen qualitativ und quantitativ das degenerierte Verhalten solcher Gleichungen -- wie z. B. die endliche Ausbreitungsgeschwindigkeit des Trägers der Lösung -- widerspiegeln.
Ein weiteres Problem in dieser Klasse ist das Fließen eines kompressiblen Bingham-Fluids in einem porösen Medium. Praktischer Hintergrund ist ein Problem in der Erdölförderung:
Eine von undurchlässigen Schichten umschlossene
ölführende Schicht steht unter Druck. Sie wird angebohrt,
und das Öl wird herausgedrückt. Zu berechnen ist die Rate, mit der dies
geschieht.
Klassische Bohrtechnologien erlauben das Anbohren einer ölführenden
Schicht nur unter Winkeln nahe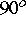 
.
In den letzten Jahren wurden Technologien entwickelt, welche es
erlauben, solche Schichten horizontal aufzuschließen.
Es ist zu klären, um wieviel effektiver ein solcher
Horizontalaufschluß im Vergleich zu einem Vertikalaufschluß sein kann.
Dieser Prozeß läßt sich durch die Gleichung
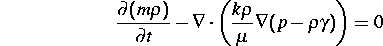
in Verbindung mit den üblichen Randbedingungen erfassen, welche die Massenbilanz des Fluids beschreibt. Die Bedeutung der Variablen ist folgende:
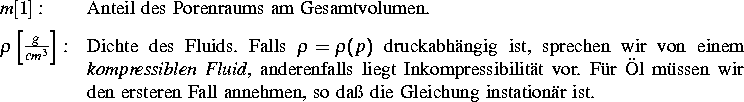
Im zu betrachtenden Falle liegt eine Entartung des Problems vor, die darin besteht, daß das Fluid bei kleinen Druckgradienten immobil wird.
