



Bearbeiter: S. Hengst, J. Fuhrmann
Kooperation: M. Wierse (Albert-Ludwigs-Universität Freiburg)
Beschreibung der Forschungsarbeit:
Gegenstand der Untersuchung ist das Ausbreitungsverhalten von (Schad)-Stoffen in porösen Medien. Aus physikalischer Sicht handelt es sich oft um Fluide, die mit Wasser nicht mischbar oder nur gering löslich sind. Sie liegen im Boden somit als getrennte Phasen vor, so daß der Durchströmungsvorgang als Mehrphasenströmungsprozeß beschrieben werden muß.
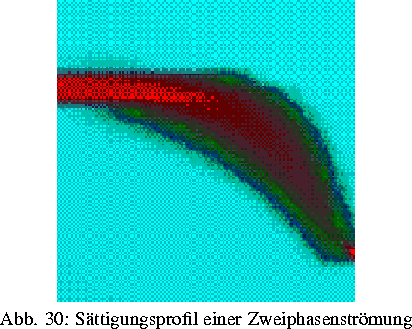
Die mathematische Formulierung einer speziellen Zweiphasenströmung (Öl, Wasser) führt auf ein gekoppeltes System elliptisch-parabolischer Differentialgleichungen. Für ein gesättigtes poröses Medium konnte die Existenz und Eindeutigkeit klassischer Lösungen des Systems ohne Einschränkung an die Raumdimension gezeigt werden und Aussagen zum asymptotischen Verhalten gegen eine stationäre Lösung aufgestellt werden. Andererseits ist dieses System nur in wenigen, stark vereinfachten Sonderfällen für analytische Lösungen zugänglich. Für eine praxisrelevante Simulation der Transportvorgänge bedarf es somit geeigneter numerischer Verfahren. Ausgehend von der Druck-Sättigungsformulierung der Strömung wurden folgende numerische Experimente durchgeführt:
