Kooperation: W. Heinrich, J. Gerdes, H. Zscheile (Ferdinand-Braun-Institut für Höchstfrequenztechnik -- FBH)
Beschreibung der Forschungsarbeit:
Der Entwurf monolithisch integrierter Schaltungen im Mikrowellen- und Millimeterwellenbereich erfordert eine dreidimensionale elektromagnetische Simulation, da mit zunehmender Packungsdichte die Kopplungsphänomene zwischen benachbarten Teilen der Schaltung berücksichtigt werden müssen und mit steigender Frequenz Gehäuseeffekte eine große Rolle spielen. Die Gehäuseabmessungen liegen in der Größenordnung der Wellenlänge. Die Schaltungen werden im GHz-Bereich (1 -- 100 GHz) im Mobilfunk, in der Radartechnik und in der Satellitenkommunikation eingesetzt.
Die dreidimensionale elektromagnetische Simulation stellt hohe Anforderungen an die räumliche Auflösung, weil einerseits Metallisierungsdicken im Mikrometerbereich und andererseits Chipdimensionen im Millimeterbereich erfaßt werden müssen.
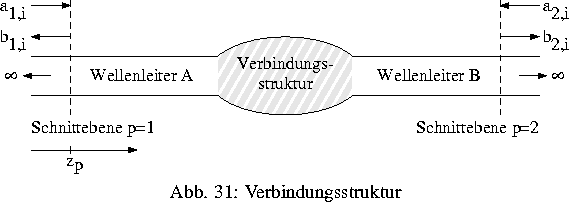
Das Transmissions- und Reflexionsverhalten der Schaltungen wird durch ihre Streumatrix beschrieben, die das Verhältnis der Amplituden der auslaufenden Moden zu den erregenden Moden darstellt. Die Streumatrix kann aus dem elektrischen Feld berechnet werden, wenn eine orthogonale Zerlegung des Feldes für ein Paar benachbarter Schnittebenen für jeden Wellenleiter für eine hinreichende Anzahl linear unabhängiger Erregungen bekannt ist (Abb. 1). Das elektromagnetische Feld wird durch die Lösung eines dreidimensionalen Randwertproblems für die Maxwellschen Gleichungen gewonnen. Es wird von der Integralform der Maxwellschen Gleichungen bei harmonischer Erregung ausgegangen, d. h., es wird im Frequenzbereich gearbeitet.
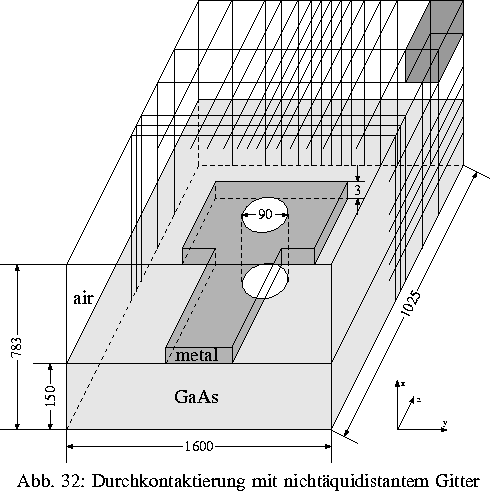
Die Diskretisierung der Gleichungen erfolgt mit Hilfe einer Finite-Volumen-Methode unter Verwendung eines kartesischen Gitters mit variabler Schrittweite (Abb. 2) und führt auf Eigenwertprobleme für schwach besetzte nichtsymmetrische Matrizen und hochdimensionale lineare Gleichungssysteme mit schwach besetzten indefiniten symmetrischen Koeffizientenmatrizen.
Das zugehörige Verfahren wird in der Elektrotechnik als FDFD-Methode (Finite-Difference Method in the Frequency Domain) bezeichnet und ist in dem Programmpaket F3D ([1], [2]) implementiert. Der Bedarf an Speicherplatz und Rechenzeit für die Simulation ist sehr hoch (bis zu 3 Wochen Rechenzeit auf modernen Workstations) und wird im wesentlichen durch die Lösung der Eigenwertprobleme und der hochdimensionalen Gleichungssysteme verursacht. Es besteht der Wunsch, kompliziertere Schaltungen zu berechnen und zur Erreichung höherer Genauigkeiten mit feinerer Diskretisierung zu arbeiten.
Folgende Arbeiten zur Verbesserung und Erneuerung der Methoden wurden durchgeführt:
1. Maßnahmen zur Verbesserung der rechenintensiven Teile des Algorithmus
Eigenwertproblem
Im Berichtsjahr 1994 wurde ein Weg gefunden, der die rechen- und speicherplatzintensive Bestimmung aller Eigenwerte zur Ermittlung einer kleinen Menge von Ausbreitungskonstanten vermeidet. Dieses Vorgehen wurde weiter vervollkommnet, so daß jetzt insgesamt Rechenzeiteinsparungen um den Faktor 45 und Speicherplatzverringerungen um den Faktor 80 erreicht werden.
Lineare Gleichungssysteme
Durch den Einsatz von Reordering-Verfahren konnten die linearen Gleichungssysteme aufgespalten werden in ein Gleichungssystem mit einer Diagonalmatrix als Koeffizientenmatrix und ein Gleichungssystem mit einer symmetrischen indefiniten Matrix, wobei die Dimension dieses Gleichungssystems wesentlich geringer ist als die des Ausgangssystems. Die dritte Maxwellsche Gleichung wird als Vorkonditionierer verwendet. So wurde die Effizienz der Verfahren gegenüber 1994 weiter gesteigert. Insgesamt konnten bis jetzt Rechenzeiteinsparungen um den Faktor 5 erzielt werden.
Eine Publikation, in der das gesamte Verfahren der feldtheoretischen Simulation von Höchstfrequenzschaltungen dargestellt ist, befindet sich in Arbeit.
2. Nichtorthogonale Diskretisierung
Die Verwendung des kartesischen Gitters mit variabler Schrittweite führt bei einer Verfeinerung in einer Region zu einer Häufung von Elementarzellen in allen Koordinatenrichtungen, die dort im allgemeinen gar nicht benötigt werden. Außerdem sind Elementarquader weniger geeignet, wenn krummlinige Ränder anzupassen sind.
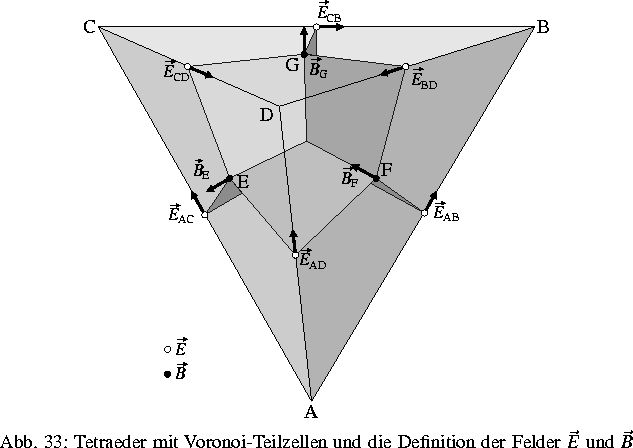
Aus diesem Grunde wurden Arbeiten begonnen, die die Verwendung von
Tetraedergittern und zugehöriger Voronoizellen als duales Gitter
anstatt von Quadergittern beinhalten (Abb. 3), um eine bessere
Anpassung des Netzes an die Problemstellung und eine Reduktion der
Dimension der Aufgaben der linearen Algebra zu erreichen.
Es wurden erste Schritte zur Formulierung der zugehörigen
Gitter-Maxwellgleichungen, zur Anpassung des Gittergenerators IGB
des WIAS (siehe S. 
) und zur Gitterverwaltung
(siehe S. ) an die Anforderungen der elektromagnetischen Simulation
gemacht.
Projektliteratur:
