



Next: Modellierung und 2D--Simulation
Up: Projekte
Previous: Nichtlineare Galerkinverfahren für
Bearbeiter: N. Bubner
Beschreibung der Forschungsarbeit:
Im vorliegenden Projekt wird an der Modellierung und Simulation von
Phasenübergängen in
[4]
Formgedächtnislegierungen gearbeitet. In SMA gibt es zwei verschiedene
stabile Gleichgewichtskonfigurationen des Metallgitters, die
temperaturabhängig sind. Der Übergang zwischen diesen beiden
Phasen, Austenit und Martensit, ist von 1. Ordnung.
gearbeitet. In SMA gibt es zwei verschiedene
stabile Gleichgewichtskonfigurationen des Metallgitters, die
temperaturabhängig sind. Der Übergang zwischen diesen beiden
Phasen, Austenit und Martensit, ist von 1. Ordnung.
Ausgangspunkt der Arbeit sind Messungen, die von
Müller und seinen Mitarbeitern seit
Jahren an der TU Berlin durchgeführt werden [1]. Sie
führen last-, temperatur- und dehnungsgesteuerte Experimente von
dünnen Stäben aus SMA durch.
Bei hohen Temperaturen verhalten sich die Proben
elastisch, bei niedrigen pseudo-
oder quasiplastisch, d.h., es werden Hysteresiskurven
gemessen. Bei
dehnungsgesteuerten Experimenten beobachtet man
außerdem, daß die
Hysteresiskurven eine innere Struktur besitzen, u.a.
können innere ,,Schleifen``
gemessen werden. Es gibt bisher kaum theoretisches
Verständnis dieser sogenannten
,,inner loops``.
In diesem Projekt wird ein von Falk für lastgesteuerte
Experimente entwickeltes
Landau-Ginzburg-Modell [vgl. 2]
auf ein dehnungsgesteuertes übertragen. Die
Wohldefiniertheit
dieses Modells wurde
analog zu [2] gezeigt.
Außerdem wurde das Kontrollproblem zur Steuerung der
Phasenübergänge formuliert.
Das numerische Verfahren zur Simulation eines von
Müller durchgeführten
dehnungsgesteuerten Experiments
[3], bestehend aus einem FE--Ansatz
mit kubischen Splines
für die Impulsbilanz, wobei die Nichtlinearitäten
nach
einer Idee von [4],
und einem voll impliziten Verfahren für die
Energiebilanz, in dem die
Nichtlinearitäten explizit behandelt werden, wurde
ausgetestet. Damit das Verfahren stabil läuft, ist
aufgrund
der enormen Unterschiede
in den Größenordnungen der Koeffizienten (bis zu
18) eine Zeitschrittweite
von bis zu 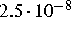 sec notwendig.
Echtzeitsimulationen von
sec notwendig.
Echtzeitsimulationen von 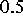 sec
benötigen auf den neuesten Workstations des Instituts
daher einige Tage bis
einige Wochen, je nach Anzahl der finiten Elemente.
sec
benötigen auf den neuesten Workstations des Instituts
daher einige Tage bis
einige Wochen, je nach Anzahl der finiten Elemente.
In den letzten 3 Monaten wurden Simulationen im
Niedrigtemperaturbereich
durchgeführt und folgende Resultate erzielt: Es gibt
zum einen nicht nur qualitativ,
sondern auch quantitativ gute Übereinstimmung mit den
Messungen.
Daraus können Schlüsse zur Bedeutung
des Ginzburg--Terms als ,,verschmierte``
Grenzflächenenergie und über die
Größe des Ginzburg--Parameters gezogen werden:
Dieser muß
groß genug gewählt werden, damit eine
Hysteresiskurve
erhalten wird. Bei zu kleinen Werten erhält man
die Maxwell--Linie. Damit stimmt das
Landau-Ginzburg-Modell
mit dem Ansatz von [5] insofern überein, daß der
Wert
des Parameters für die Kohärenzenergie für die
Größe der Hysteresis bestimmend ist. Ebenso
können Beziehungen zu theoretischen
Überlegungen von Rogers et al. [u.a. 6] hergestellt
werden.
In diesen Arbeiten wird ein
neues Modell vorgestellt, welches als Spezialfälle zum
einen den Landau--Ginzburg--Ansatz enthält, zum
anderen dem
Ansatz von [5] entspricht.
Weiterhin erhalten wir Zugang zur inneren Struktur der
Hysteresiskurven. Die Simulationen stimmen
größtenteils mit den Messungen (auch
mit experimentellen Resultaten, die man im
Ferromagnetismus erhält
[3]) qualitativ überein.
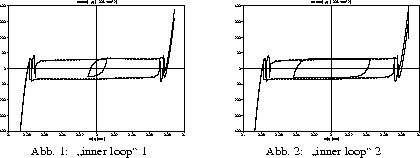
In den Abbildungen 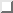 und
und  ist die numerisch berechnete innere Spannung
ist die numerisch berechnete innere Spannung  am
Rand eines
SMA--Drahtes (Länge des Drahtes: 1 cm)
gegenüber der Dehnung
am
Rand eines
SMA--Drahtes (Länge des Drahtes: 1 cm)
gegenüber der Dehnung 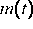 , die an diesem Rand von
außen vorgegeben wird, aufgetragen.
Die Abbildungen zeigen jeweils die ,,äußere``
Hysteresis mit zwei verschieden
großen ,,inner loops``.
Besonders bei dem größeren ,,inner loop``
(Abb.
, die an diesem Rand von
außen vorgegeben wird, aufgetragen.
Die Abbildungen zeigen jeweils die ,,äußere``
Hysteresis mit zwei verschieden
großen ,,inner loops``.
Besonders bei dem größeren ,,inner loop``
(Abb. ) wird die innere Struktur der Hysteresis
sichtbar.
Abbildung
) wird die innere Struktur der Hysteresis
sichtbar.
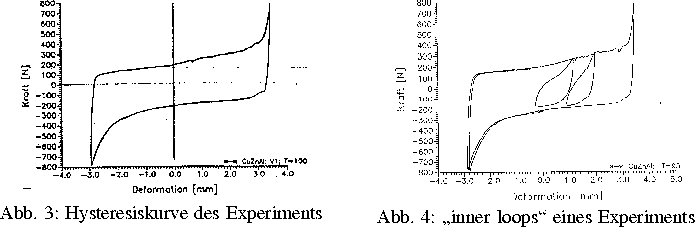
Abbildung  zeigt die gemessene Hysteresiskurve,
mit der die physikalischen Parameter für die
numerischen Simulationen
geeicht wurden und die auch quantitativ gut mit den
Simulationen
übereinstimmt (Länge des Drahtes: 3.4 cm; um die
Abbildungen
vergleichen zu können, müssen wegen
zeigt die gemessene Hysteresiskurve,
mit der die physikalischen Parameter für die
numerischen Simulationen
geeicht wurden und die auch quantitativ gut mit den
Simulationen
übereinstimmt (Länge des Drahtes: 3.4 cm; um die
Abbildungen
vergleichen zu können, müssen wegen 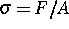 ,
A:
Querschnitt des Stabes, die gemessenen Werte für die
Kraft noch
durch 4.5 dividiert werden).
Abbildung
,
A:
Querschnitt des Stabes, die gemessenen Werte für die
Kraft noch
durch 4.5 dividiert werden).
Abbildung  zeigt typische Beispiele von
inneren Loops.
zeigt typische Beispiele von
inneren Loops.
Projektliteratur:
- Y. Huo, I. Müller, Nonequilibrium
Thermodynamics of
Pseudoelasticity, Cont. Mech. Thermodyn. 5
(1993) 163--204.
- J. Sprekels, S. Zheng, Global Solutions to
the Equations
of a Ginzburg--Landau Theory for structural Phase
Transitions in
Shape Memory Alloys, Physica D 39 (1989)
59--76.
- I. Müller, private communication.
- M. Niezgódka, J. Sprekels, Convergent
numerical
approximations of the thermomechanical phase
transitions in shape
memory alloys, Numer. Math. 58 (1991)
759--778.
- S. Fu, Y. Huo, I. Müller, Thermodynamics
of
pseudoelasticity -- an analytical approach, Acta
Mech. 99 (1993)
1--19.
- T. Lin, R. Rogers, Computation of Phase
Transitions Using
Nonlocal Regularization,
ICAM report 93--09--03,
Virginia
Polytechnic Insitute and State University,
Blacksburg
[3] (1993).




Next: Modellierung und 2D--Simulation
Up: Projekte
Previous: Nichtlineare Galerkinverfahren für
BREMERO
Wed Apr 12 21:47:02 MDT 1995
 gearbeitet. In SMA gibt es zwei verschiedene
stabile Gleichgewichtskonfigurationen des Metallgitters, die
temperaturabhängig sind. Der Übergang zwischen diesen beiden
Phasen, Austenit und Martensit, ist von 1. Ordnung.
gearbeitet. In SMA gibt es zwei verschiedene
stabile Gleichgewichtskonfigurationen des Metallgitters, die
temperaturabhängig sind. Der Übergang zwischen diesen beiden
Phasen, Austenit und Martensit, ist von 1. Ordnung.




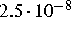 sec notwendig.
Echtzeitsimulationen von
sec notwendig.
Echtzeitsimulationen von 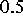 sec
benötigen auf den neuesten Workstations des Instituts
daher einige Tage bis
einige Wochen, je nach Anzahl der finiten Elemente.
sec
benötigen auf den neuesten Workstations des Instituts
daher einige Tage bis
einige Wochen, je nach Anzahl der finiten Elemente.


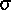 am
Rand eines
SMA--Drahtes (Länge des Drahtes: 1 cm)
gegenüber der Dehnung
am
Rand eines
SMA--Drahtes (Länge des Drahtes: 1 cm)
gegenüber der Dehnung 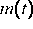 , die an diesem Rand von
außen vorgegeben wird, aufgetragen.
Die Abbildungen zeigen jeweils die ,,äußere``
Hysteresis mit zwei verschieden
großen ,,inner loops``.
Besonders bei dem größeren ,,inner loop``
(Abb.
, die an diesem Rand von
außen vorgegeben wird, aufgetragen.
Die Abbildungen zeigen jeweils die ,,äußere``
Hysteresis mit zwei verschieden
großen ,,inner loops``.
Besonders bei dem größeren ,,inner loop``
(Abb.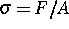 ,
A:
Querschnitt des Stabes, die gemessenen Werte für die
Kraft noch
durch 4.5 dividiert werden).
Abbildung
,
A:
Querschnitt des Stabes, die gemessenen Werte für die
Kraft noch
durch 4.5 dividiert werden).
Abbildung