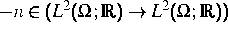




Bearbeiter: H. Gajewski, H.--Chr. Kaiser, J. Rehberg, H. Stephan
Kooperation: Doz. Dr. H.--J. Wünsche, Humboldt--Universität zu
Berlin, Institut für Physik;
Dr. Friedland, Dr. Kleinert,
Paul--Drude--Institut für Festkörperelektronik, Berlin;
Dr. W. Heinrich, H. Wenzel, Ferdinand--Braun--Institut
für Höchstfrequenztechnik, Berlin
Beschreibung der Forschungsarbeit:
Bei Halbleiterschichten, deren Dicken im Nanometerbereich liegen -- sogenannten Nanostrukturen -- und damit klein sind im Vergleich zur Elektronenwellenlänge spielen Quanteneffekte eine entscheidende Rolle. Praktisch werden solche Effekte in Halbleiterbauelementen seit geraumer Zeit erfolgreich ausgenutzt. Speziell in Laserdioden bestehen die aktiven Zonen häufig aus Quantum Wells (QW). In Nanostrukturen können sich die Ladungsträger nicht mehr in allen drei Raumrichtungen bewegen und die Vorstellung vom Elektronengas im dreidimensionalen Raum ist nicht mehr adäquat; stattdessen liegt ein zwei--, ein-- oder nulldimensionales Elektronengas vor. Bei der Modellierung von Halbleiterbauelementen mit reduzierter Dimension ist man genötigt, einen quantenmechanisch motivierten Ausdruck für die Ladungsträgerdichten im Bauelement zugrunde zu legen. Bereits bei der Untersuchung der Grenzfläche zweier verschiedener Halbleitermaterialien in Heterostrukturen können quantenmechanische Phänomene eine wesentliche Rolle spielen. Ein geeignetes Modell für Halbleiterbauelemente mit reduzierter Dimension ist das Schrödinger--Poisson--System [2, 3, 1].
In [3]
haben wir gezeigt,
daß der negative quantenmechanische Elektronendichteoperator
ein beschränkt Lipschitzstetiger Operator
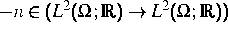
ist. Dies impliziert die gleichmäßige Konvergenz des Gradientenverfahrens für das Schrödinger--Poisson--System und erlaubt damit Abschätzungen für die Elektronenenergien (Eigenwerte des Schrödingeroperators) [3, 4]. Unsere numerische Behandlung des zweidimensionalen Schrödinger--Poisson--Systems beruht auf diesen Resultaten.
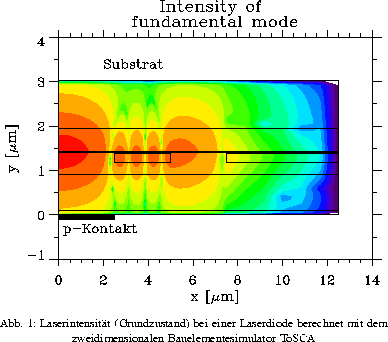
Zur numerischen Simulation von mikroelektronischen Bauelementen wird zumeist wie auch beim 2D--Bauelementesimulator ToSCA das van Roosbroeck--System von partiellen Differentialgleichungen der inneren Elektronik zweidimensional gelöst. Für die Simulation von Strukturen mit Quantum Wells ist das klassische Grundgleichungssystem um quantenmechanische Gleichungen (Schrödinger--Poisson--System für zwei Ladungsträgersorten mit Kohn-Sham Vielteilchenpotential sowie Transportgleichungen) zu erweitern. Diese gelten dann allerdings nur in mikroskopisch kleinen Bereichen und sind auf konsistente Weise in das makroskopische Problem einzubetten, z.B. durch kinetische Gleichungen. Die Lösung dieser Problemstellung ist von prinzipieller Bedeutung nicht nur für viele Typen von Halbleiterlasern sondern auch für andere mikro- und optoelektronische Bauelemente. Erstmals wird dabei die Quantenmechanik von QW-Schichten adäquat in eine 2D-Simulation einbezogen. Die Anwendung dieser Berechnungen ist in zwei konkreten Fällen vorgesehen:
(i) Hochleistungs-Laserdioden, die speziell in der Materialbearbeitung und in der Medizintechnik eingesetzt werden, sowie Pump--Laser für optische Faserverstärker der Informations-- und Kommunikationstechnik. (ii) Oberflächenemittierende Laserdioden (VCSEL), die vor allem in der optischen Verbindungstechnik und Signalverarbeitung zum Einsatz kommen.
Beim Einsatz und der numerischen Bewertung von Standard--Software für die Lösung des Eigenwertproblems im Schrödinger--Poisson--System werden wir von Dr. G. Hebermehl und G. Reinhardt aus der Forschungsgruppe ,,Numerische Mathematik und Wissenschaftliches Rechnen`` unterstützt.
Förderung: BMBF-Förderprogramm Anwendungsorientierte Verbundprojekte auf dem Gebiet der Mathematik
Projektliteratur:



