A Basic Definitions
This section gives simplified explanations of some basic notions of
combinatorial topology as a quick reference.
A.1 Simplices, Simplicial Complexes
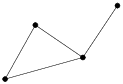
| Figure 25: (a) A two-dimensional simplicial complex K consists of
2 triangles(which are shaded), 7 edges, and 5 vertices. (b) The underlying space. (c) A subcomplex, which is a
1-dimensional simplicial complex, consists of 4 edges, and 4
vertices. |
Convex Hull
A point set V ⊂ ℝd is convex if it contains every line segment whose end points are in this set. There are infinitely many convex sets containing V. The smallest convex set containing V is called the convex hull of V, denoted as convV. The dimension of the convex hull of V is the dimension of the affine space of V.
Simplex
A simplex σ is the convex hull of an affinely independent
set S of points. The dimension of σ is one less than
the number of points of S. Specifically, in ℝ3 the
maximum number of affinely independent points is 4, so we have
non-empty simplices of dimensions 0, 1, 2 and 3 referred to as
vertices, edges, triangles, and tetrahedra,
respectively. For any subset T ⊆ S, the simplex τ =
convT is a face of σ and we write τ ≤
σ. τ is a proper face of σ if T is a proper
subset of S.
simplicial Complex
A simplicial complex K is a finite set of simplices such that
(i) any face of a simplex in K is also in K, and (ii) the
intersection of any two simplices in K is a face of both. Condition
(ii) allows for the case in which two simplices are disjoint because
the empty set is the unique (-1)-dimensional simplex, which is a face
of any simplex. Figure 25 (a) illustrates a
two-dimensional simplicial complex.
Underlying Space
The underlying space of a set of simplices L, denoted |L|,
is the union of simplices, ∪σ ∈ Lσ (see an
illustration in Figure 25 (b)). |L| is a
topologically closed set if and only if L is a simplicial complex.
Subcomplex
A subcomplex of K is a subset of simplices of K that is also
a simplicial complex. For an example see
Figure 25 (c).
A.2 Polyhedra and Faces
Convex polyhedra and their faces are well defined objects. It is a central topic in discrete geometry to study their structures and properties, see [29]. However, general polyhedra which are not necessarily convex are much complex objects. There exist various definitions in the literature. We adopt the definitions given by Edelsbrunner [7].
A polyhedron P is the union of convex polyhedra and the space of P is connected. It is not necessarily convex, see Figure 26 left for an example. The dimension of P is the dimension of the smallest affine space that contains P. The interior of P, denoted as int(P) is the point set such that every point p ∈ int(P) has a neighborhood (e.g., an open ball centered at this point) which is a subset of P. The boundary of P is the point set bd(P) = P − int(P).
A face F of P satisfies the following three conditions:
-
(1) F is the closure of a connected set of points;
- (2) F is contained in the boundary of P; and
- (3) F is equal to the intersection of P with the minimal affine space containing F.
F is also a polyhedron whose dimension is the dimension of the affine space that determines F. 0-, 1-, and 2-dimensional faces of P are called vertices, edges, and facets of P. Each facet is a polygonal region which may not be convex and may contain holes in it, as illustrated in the right of Figure 26.
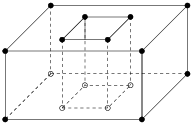
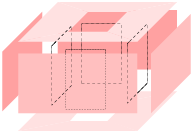
| Figure 26: A three-dimensional non-convex polyhedron. In left, the vertices (0-faces) and edges (1-faces) of the polyhedron are shown. All its facets (2-faces) are shown in right. |
A.3 CSG and B-Rep Models of 3d Domains
In geometric and solid modeling, constructive solid geometry (CSG) and boundary representation (B-Rep) are two popular representations for three-dimensional objects.
A CSG model implicitly describes the domain as a combination of simple primitives or other solids in a series of Boolean operations. It can describe rather complicated shapes simply. However, the domain boundary must be calculated numerically in order to find the intersecting points, curves, and patches. This involves solving many non-linear equations in three variables. Obtaining a PLC from a CSG model is generally not a simple task.
A B-Rep model explicitly describes the domain boundary by a set of non-overlapping facets (may be curved surfaces) together with topological information (such as incidence and adjacency) between the facets. The volume of the domain is implicitly bounded by them. However, it is not trivial to correctly define such a model for a complex object. Nevertheless, The B-Rep model is popularly used in describing 3d geometries.