Robustness of mixed FE methods for

[Next]:

Simulation of microwave and semiconductor laser

[Up]:

Projects

[Previous]:

Three-dimensional unsteady melt-flow simulation in Czochralski

[Contents]

[Index]

Subsections

Robustness of mixed FE methods for a generalized Stokes equation

Collaborator: H. Langmach

Cooperation with: A. Linke (Freie Universität Berlin (DFG Research Center MATHEON))

Supported by: DFG Research Center MATHEON, project C2

Description: One important application for solving the Navier-Stokes equation at WIAS has been the flow simulation of crystal melts in Czochralski crystal growth. This research is continued by the project C2 at the DFG Research Center MATHEON.

The simulation of crystal growth makes very high demands on available computing time. Typically, the three-dimensional simulation of small model problems for industrial crystal growth with our efficient Navier-Stokes solver NAVIER needs computing time in the order of weeks.

This has to be reduced by new software techniques delivered by pdelib2 and new mathematical methods and algorithms.

On the mathematical side the focus lies on robust discretization and robust iterative solvers for the Navier-Stokes equations. As shown below, the standard Taylor-Hood ( P^k+1 - P^k) discretization for the Navier-Stokes equation does not fully accomplish these robustness requirements. Therefore, we consider alternative discretization methods. We started with the implementation and investigation of the stabilized P1-P1 element. This element is used for preconditioning purposes.

Non-robustness of the Taylor-Hood element

Let us look at the following simple model problem, a stationary generalized Stokes problem:

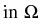- $\displaystyle {\frac{{1}}{{\mathit{Re}}}}$ $\displaystyle \Delta$ u + $\displaystyle \nabla$ p	=	f $\displaystyle \mbox{in $\Omega$}$ ,
$\displaystyle \nabla$ ^.u	=	0 $\displaystyle \mbox{in $\Omega$}$ ,	(1)
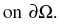u	=	0 $\displaystyle \mbox{on $\partial \Omega$.}$

Let (u^h, p^h) denote the discrete solution of (1) obtained by the Taylor-Hood ( P^k+1 - P^k) mixed finite element method. Then one can derive the following a priori FEM error estimate 1

h|u - u^h|_H¹ + ||u - u^h||_L² 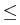$\displaystyle \leq$ Ch²(|u|_H² + Re| p|_H¹),

(2)

where C depends on $\Omega$ . In the case that Re is high, the second term in the error estimate possesses a large weighting factor. This effect can be reproduced numerically ([1]) and is not limited to the Taylor-Hood element family. For the Navier-Stokes equation, one can make a similiar observation.

Robustness of the P1-P1-stab element

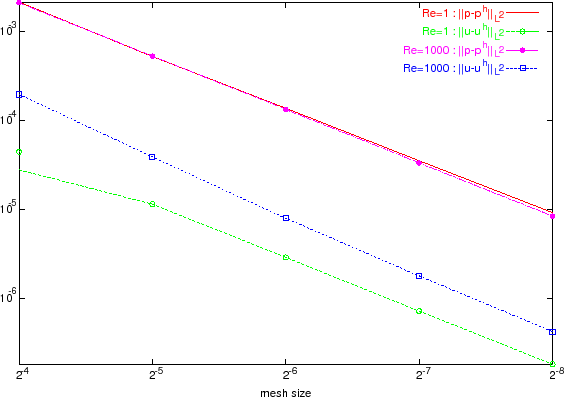
In 2004, the implementation of a stabilized P1-P1 element for Stokes equations using pdelib2 has been completed. This will be used for preconditioning by algebraic multigrid methods. Stabilized P1-P1 elements have interesting robustness properties in respect of high Reynolds number flow ([2]), but have a low approximation order. The robustness is shown by the following numerical study. The example is taken from [1] and is typical for the kind of investigated problems. We look for a numerical solution of [1] with Re = 1 and Re = 1000 in the unit square $\Omega$ = [0, 1]². 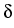$\delta$ is the respective optimal stability parameter. We prescribe the solution to u = (u₁, u₂) and p given by

u₁(x, y)	=	2x²(1 - x)²(y(1 - y)² - y²(1 - y))
u₂(x, y)	=	-2y²(1 - y)²(x(1 - x)² - x²(1 - x))
p(x, y)	=	x³ + y³ - 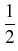$\displaystyle {\frac{{1}}{{2}}}$ .

$\begin{figure}\ProjektEPSbildNocap{0.8\textwidth}{linke2004.eps} \end{figure}$

References:

S. GANESAN, V. JOHN, Pressure separation -- A technique for improving the velocity error in finite element discretisations of the Navier-Stokes equations, to appear in: Appl. Math. Comput.
G. LUBE, M.A. OLSHANSKII, Stable finite-element calculation of incompressible flows using the rotation form of convection, IMA J. Numer. Anal., 22 (2002), pp. 437-461.