Three-dimensional unsteady melt-flow simulation in Czochralski

[Next]:

Robustness of mixed FE methods for

[Up]:

Projects

[Previous]:

Numerical investigation of the non-isothermal contact

[Contents]

[Index]

Three-dimensional unsteady melt-flow simulation in Czochralski crystal growth

Collaborator: D. Davis, H. Langmach, G. Reinhardt

Cooperation with: K. Böttcher, W. Miller, U. Rehse (Institut für Kristallzüchtung, Berlin)

Description:

In 2004 we continued a collaborative project with the Institute for Crystal Growth (IKZ) in Berlin, involving the numerical unsteady flow simulation of semiconductor (GaAs) melt in a vapor-pressure-controlled Czochralski crucible (cf. previous two annual reports; also [1], [2]).

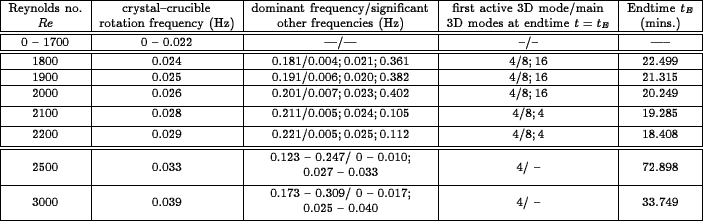
As explained in the above references, the melt-flow behavior and temperature distribution in the crucible are pivotal features which ultimately determine the shape of the crystallization front (see also [3], [4]). Our previous work on GaAs melt-flow simulation concentrated on fully transient flows and their associated time-averaged properties (WIAS Annual Report 2002 , [2]). More recently, we have been concerned with understanding the underlying instability mechanisms, including weakly-nonlinear mode interaction, to provide a more rational explanation for the complex unsteady processes hitherto observed. (A similar procedure has been used in our InP study (WIAS Annual Report 2003 )). After first establishing that the critical Reynolds number (marking the onset of unsteady flow) occurred in the range (1700, 1800), we focused on five cases (Re = 1800, 1900, 2000, 2100, 2200), which all demonstrated oscillatory flow behavior. A Fourier mode analysis was applied to determine the time evolutions of individual azimuthal modes, whereas the dominant frequencies were found by means of discrete Fourier transformations. In Table 1, the dominant frequencies are shown; here we have also included the results from some fully transient cases (Re = 2500, 3000), where pointwise frequencies were no longer discernible, reflecting the relatively ``chaotic'' flow behavior in these cases.

$\begin{figure}\ProjektEPSbildNocap{0.9\textwidth}{table4.eps} \end{figure}$

Table 1: Major frequency responses and principal azimuthal modes for three-dimensional numerical simulations in flat-based crucibles; for the transient cases ( Re = 2500, 3000) the major frequency clusters are noted. For the oscillatory cases (Re = 1800 - 2200) the dominant frequency stems from the m = 8 mode, and the significant other frequencies (in order of size, smallest first) from the axisymmetric mode, the m = 1 mode (which solely dominates the horizontal-velocity behavior near the axis), and either the first higher harmonic or subharmonic of the m = 8 mode. The dimensional values in the table are determined using a crucible radius R_C = 0.077 m, and kinematic viscosity $\nu$ = 4.88 x 10^-7m²s^-1 (Rehse et al. [4]).

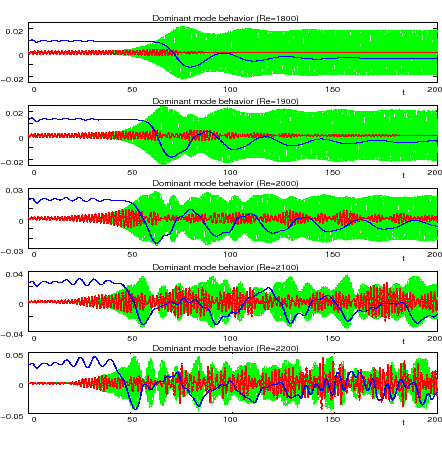
It is clear from the oscillatory cases that the most unstable linear mode is m = 4, but as demonstrated in Figure 1, the dominance of this mode is short-lived, and it quickly gives way to the (nonlinearly-induced) modes m = 8 and m = 16; in this figure, we have focused on the temperature at the point (0.75*R_C, 0.33*H), where R_C is the radius of the crucible and H is the height of the melt ( H = 0.3 x R_C), but we note that the general pattern of behavior observed here is essentially unchanged for other quantities and at other non-axial locations within the crucible.

**Fig. 1:** Time histories of the Fourier cosine modes m = 0 (dark), 4 (medium dark), 8 (light) of the temperature at ( 0.75 `x` R_C, 0.33 `x` H) for Re = 1800 - 2200 with Gr = 1.36 `x` Re² in each case
$\ProjektEPSbildNocap{0.5\textwidth}{fig1_c.eps}$

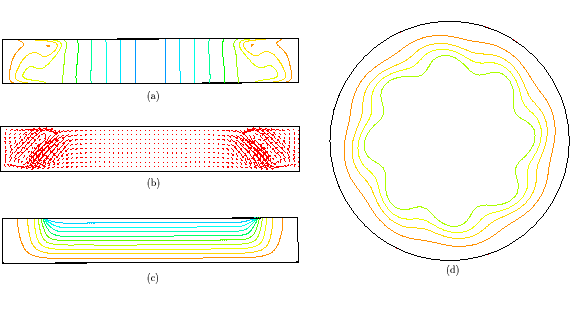
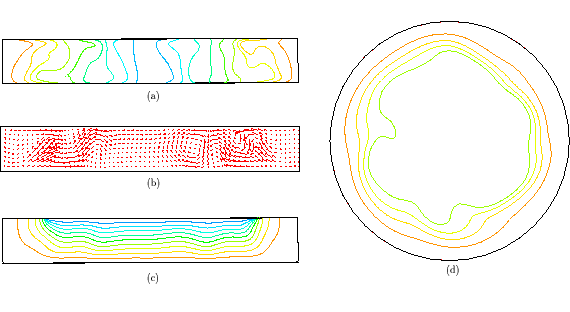
In Figure 2, a snapshot of the temperature is given for the case Re = 1800, where the importance of the m = 8 mode can clearly be seen. (Some higher harmonics---m = 8k_i, i = 1,..., r, say---are also active we note, but these do not affect the observed 8-fold azimuthal symmetry, since the greatest common divisor of the dominant modes is 8, i.e. gcd( 8, 8k₁,..., 8k_r)=8.) In contrast, for Re = 2500 no such simple periodic behavior can be observed (see Figure 3).

**Fig. 2:** Snapshots at t = 193.2 for iso-rotation with Re = 1800, Gr = 4.4064 `x` 10⁶. Results show (a) azimuthal velocity component, (b) velocity projection, (c) temperature contours, all in the same vertical plane, and (d) temperature contours in the midheight plane ( 0.5 `x` H). In (a) the contours range from 0 (axis) to 1 (wall), in (c) from 0 (crystal) to 1 (wall/base), and in (d) decrease in value inwards from wall (value 1), in each case in intervals of 0.1.
$\ProjektEPSbildNocap{0.7\textwidth}{fig2_c.eps}$

**Fig. 3:** Snapshots at t = 535 for iso-rotation with Re = 2500, Gr = 8.5 `x` 10⁶. Results show (a) azimuthal velocity component, (b) velocity projection, (c) temperature contours, all in the same vertical plane, and (d) temperature contours in the midheight plane ( 0.5 `x` H). In (a) the contours decrease in value from 1 (wall), in (c) they range from 0 (crystal) to 1 (wall/base), and in (d) they decrease in value inwards from wall (value 1), in each case in intervals of 0.1.
$\ProjektEPSbildNocap{0.7\textwidth}{fig3_c.eps}$

References:

E. BÄNSCH, D. DAVIS, H. LANGMACH, W. MILLER, U. REHSE, G. REINHARDT, M. UHLE, Axisymmetric and 3D calculations of melt-flow during VCz growth, J. Crystal Growth, 266 (2004), pp. 60-66.
E. BÄNSCH, D. DAVIS, H. LANGMACH, G. REINHARDT, M. UHLE, Two- and tree-dimensional transient melt-flow simulation in vapour-pressure-controlled Czochralski crystal growth, 2004, submitted.
W. MILLER, U. REHSE, Numerical simulation of temperature and flow field in the melt for the vapour-pressure-controlled Czochralski growth of GaAs, Crys. Res. Technol., 36 (2001), pp. 685-694.
U. REHSE, W. MILLER, CH. FRANK, P. RUDOLPH, M. NEUBERT, A numerical investigation of the effects of iso- and counter-rotation on the shape of the VCz growth interface, J. Crystal Growth, 230 (1997), pp. 143-147.