Simulation of microwave and semiconductor laser

[Next]:

Process simulation in gas turbine engineering

[Up]:

Projects

[Previous]:

Robustness of mixed FE methods for

[Contents]

[Index]

Simulation of microwave and semiconductor laser structures including perfectly matched layer by means of FIT

Collaborator: G. Hebermehl, R. Schlundt

Cooperation with: W. Heinrich, Th. Tischler (Ferdinand-Braun-Institut für Höchstfrequenztechnik, Berlin (FBH))

Description:

The electromagnetic simulation plays an indispensable part in the development of microwave circuits as well as in diode laser design, [6, 7]. Commonly the electromagnetic characteristics of the structures are described by their scattering matrix which is extracted from the orthogonal decomposition of the electric field at a pair of neighboring cross-sectional planes on each waveguide, [2]. The electric field is the solution of a two-dimensional eigenvalue and a three-dimensional boundary value problem for Maxwell's equations in the frequency domain, [4]. The surface of the computation domain is assumed to be an electric or a magnetic wall. Open-region problems require uniaxial Perfectly Matched Layer (PML) absorbing boundary conditions. At the ports, p the transverse mode field is given by superposing transmission line modes.

**Fig. 1:** The basic structure under investigation
$\ProjektEPSbildNocap{0.90\textwidth}{f3dgrid_5_7.eps}$

The subject under investigation can be represented by the basic description shown in Figure 1, a structure of arbitrary geometry which is connected to the remaining circuit by transmission lines. The passive structure (discontinuity) forms the central part of the problem. Short transmission line sections are attached to it in order to describe its interaction with other circuit elements, [4].

A three-dimensional boundary value problem can be formulated using the integral form of Maxwell's equations in the frequency domain, [1]. The Maxwell equations are discretized with orthogonal grids using the Finite Integration Technique (FIT), [1, 3, 9].

$\displaystyle \oint_{{\partial \Omega}}^{}$ $\displaystyle \vec{E}$ ^.d $\displaystyle \vec{s}$	=	-j $\displaystyle \omega$ $\displaystyle \int_{{\Omega}}^{}$ $\displaystyle \vec{B}$ ^.d $\displaystyle \vec{\Omega}$ ,	$\displaystyle \oint_{{\Omega}}^{}$ $\displaystyle \vec{B}$ ^.d $\displaystyle \vec{\Omega}$	=	0,
$\displaystyle \oint_{{\partial \Omega}}^{}$ $\displaystyle {\frac{{1}}{{(\mu)}}}$ $\displaystyle \vec{B}$ ^.d $\displaystyle \vec{s}$	=	j $\displaystyle \omega$ $\displaystyle \int_{{\Omega}}^{}$ ( $\displaystyle \epsilon$ ) $\displaystyle \vec{E}$ ^.d $\displaystyle \vec{\Omega}$ ,	$\displaystyle \oint_{{\Omega}}^{}$ ( $\displaystyle \epsilon$ ) $\displaystyle \vec{E}$ ^.d $\displaystyle \vec{\Omega}$	=	0,

$\displaystyle \vec{D}$ = ( $\displaystyle \epsilon$ ) $\displaystyle \vec{E}$ , $\displaystyle \vec{B}$ = ( $\displaystyle \mu$ ) $\displaystyle \vec{H}$ ,( $\displaystyle \epsilon$ ) = diag $\displaystyle \left(\vphantom{ {\epsilon}_x, {\epsilon}_y, {\epsilon}_z }\right.$ $\displaystyle \epsilon_{{x}}^{{}}$ , $\displaystyle \epsilon_{{y}}^{{}}$ , $\displaystyle \epsilon_{{z}}^{{}}$ $\displaystyle \left.\vphantom{ {\epsilon}_x, {\epsilon}_y, {\epsilon}_z }\right)$ ,( $\displaystyle \mu$ ) = diag $\displaystyle \left(\vphantom{ {\mu}_x, {\mu}_y, {\mu}_z }\right.$ $\displaystyle \mu_{{x}}^{{}}$ , $\displaystyle \mu_{{y}}^{{}}$ , $\displaystyle \mu_{{z}}^{{}}$ $\displaystyle \left.\vphantom{ {\mu}_x, {\mu}_y, {\mu}_z }\right)$ .

For the PML region in x direction, the effective permittivity and permeability are represented as follows:

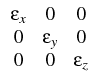
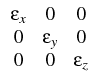
( $\displaystyle \epsilon$ ) = $\displaystyle \left(\vphantom{ \begin{array}{ccc} \epsilon_{x} & 0 & 0 \ 0 & \epsilon_{y} & 0 \ 0 & 0 & \epsilon_{z} \end{array} }\right.$ $\displaystyle \begin{array}{ccc} \epsilon_{x} & 0 & 0 \ 0 & \epsilon_{y} & 0 \ 0 & 0 & \epsilon_{z} \end{array}$ $\displaystyle \left.\vphantom{ \begin{array}{ccc} \epsilon_{x} & 0 & 0 \ 0 & \epsilon_{y} & 0 \ 0 & 0 & \epsilon_{z} \end{array} }\right)$ $\displaystyle \longrightarrow$ ( $\displaystyle \epsilon$ )[ $\displaystyle \Lambda$ ]_x = $\displaystyle \left(\vphantom{ \begin{array}{ccc} \epsilon_{x} & 0 & 0 \ 0 & \epsilon_{y} & 0 \ 0 & 0 & \epsilon_{z} \end{array} }\right.$ $\displaystyle \begin{array}{ccc} \epsilon_{x} & 0 & 0 \ 0 & \epsilon_{y} & 0 \ 0 & 0 & \epsilon_{z} \end{array}$ $\displaystyle \left.\vphantom{ \begin{array}{ccc} \epsilon_{x} & 0 & 0 \ 0 & \epsilon_{y} & 0 \ 0 & 0 & \epsilon_{z} \end{array} }\right)$ $\displaystyle \left(\vphantom{ \begin{array}{ccc} \frac{1}{\lambda_{\epsilon}} ... ... 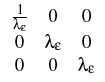0 & \lambda_{\epsilon} & 0 \ 0 & 0 & \lambda_{\epsilon} \end{array} }\right.$ $\displaystyle \begin{array}{ccc} \frac{1}{\lambda_{\epsilon}} & 0 & 0 \ 0 & \lambda_{\epsilon} & 0 \ 0 & 0 & \lambda_{\epsilon} \end{array}$ $\displaystyle \left.\vphantom{ \begin{array}{ccc} \frac{1}{\lambda_{\epsilon}} ... ... 0 & \lambda_{\epsilon} & 0 \ 0 & 0 & \lambda_{\epsilon} \end{array} }\right)$ ,

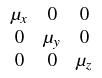
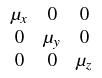
( $\displaystyle \mu$ ) = $\displaystyle \left(\vphantom{ \begin{array}{ccc} \mu_{x} & 0 & 0 \ 0 & \mu_{y} & 0 \ 0 & 0 & \mu_{z} \end{array} }\right.$ $\displaystyle \begin{array}{ccc} \mu_{x} & 0 & 0 \ 0 & \mu_{y} & 0 \ 0 & 0 & \mu_{z} \end{array}$ $\displaystyle \left.\vphantom{ \begin{array}{ccc} \mu_{x} & 0 & 0 \ 0 & \mu_{y} & 0 \ 0 & 0 & \mu_{z} \end{array} }\right)$ $\displaystyle \longrightarrow$ ( $\displaystyle \mu$ )[ $\displaystyle \Lambda$ ]_x = $\displaystyle \left(\vphantom{ \begin{array}{ccc} \mu_{x} & 0 & 0 \ 0 & \mu_{y} & 0 \ 0 & 0 & \mu_{z} \end{array} }\right.$ $\displaystyle \begin{array}{ccc} \mu_{x} & 0 & 0 \ 0 & \mu_{y} & 0 \ 0 & 0 & \mu_{z} \end{array}$ $\displaystyle \left.\vphantom{ \begin{array}{ccc} \mu_{x} & 0 & 0 \ 0 & \mu_{y} & 0 \ 0 & 0 & \mu_{z} \end{array} }\right)$ $\displaystyle \left(\vphantom{ \begin{array}{ccc} \frac{1}{\lambda_{\mu}} & 0 & 0 \ 0 & \lambda_{\mu} & 0 \ 0 & 0 & \lambda_{\mu} \end{array} }\right.$ $\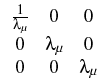displaystyle \begin{array}{ccc} \frac{1}{\lambda_{\mu}} & 0 & 0 \ 0 & \lambda_{\mu} & 0 \ 0 & 0 & \lambda_{\mu} \end{array}$ $\displaystyle \left.\vphantom{ \begin{array}{ccc} \frac{1}{\lambda_{\mu}} & 0 & 0 \ 0 & \lambda_{\mu} & 0 \ 0 & 0 & \lambda_{\mu} \end{array} }\right)$ ,

with $\lambda_{{\epsilon}}^{}$ = 1 - j $\displaystyle {\frac{{\kappa_{\epsilon}}}{{\epsilon_{0}\omega}}}$ , $\lambda_{{\mu}}^{}$ = 1 - j $\displaystyle {\frac{{\kappa_{\mu}}}{{\mu_{0}\omega}}}$ , and $\displaystyle {\frac{{\kappa_{\epsilon}}}{{\epsilon_{0}}}}$ = $\displaystyle {\frac{{\kappa_{\mu}}}{{\mu_{0}}}}$ .
For edges, for example, an edge in z direction, the values ( $\epsilon$ ) and ( $\mu$ ) should be chosen so that ( $\epsilon$ ) $\longrightarrow$ ( $\epsilon$ )[ $\Lambda$ ]_x[ $\Lambda$ ]_y and ( $\mu$ ) $\longrightarrow$ ( $\mu$ )[ $\Lambda$ ]_x[ $\Lambda$ ]_y, respectively. For corners, the ( $\epsilon$ ) and ( $\mu$ ) will be the product of the tensors in all three directions.

$\bullet$ Eigenmode problem [2]: In order to compute the three-dimensional boundary value problem, the transverse mode fields at the ports p (see Figure 1) have to be known. The transverse mode fields are the solutions of an eigenvalue problem. The sparse matrix is generally complex. The solutions of the eigenvalue problem correspond to the propagation constants of the modes. Using a conformal mapping, it can be shown that the eigenvalues corresponding to the few interesting modes of smallest attenuation are located in a region bounded by two parabolas. Because of the high wavenumber we can find, in general, the interesting modes only covering the region with s circles and calculating the eigenvalues located in these circles.

Especially, for diodes, laser frequencies of several hundred THz are common. That means, a significantly higher number of high-dimensional eigenvalue problems has to be solved with our algorithm. Additionally, using PML, the number of eigenmodes to be calculated and the iteration number of the applied Arnoldi algorithm increase. Thus, the number s of modified eigenvalue problems to be solved is controlled ([5]) restricting the number of required eigenvalues in one circle, the number of iterations of the Arnoldi method, and the overlapping size of the circles. The s eigenvalue problems can be solved in parallel.

$\bullet$ Boundary value problem [1]: The electromagnetic fields are computed by the solution of large-scale systems of linear equations with indefinite, complex symmetric coefficient matrices. Independent set orderings, Jacobi and SSOR preconditioning using Eisenstat's trick are applied to accelerate the speed of convergence of the used Krylov subspace method [4, 8] for the systems of linear algebraic equations.

The PML layers have a significant influence on computational efforts, which is demonstrated in Table 1 for a quasi-TEM waveguide.

Table: Influence of the PML layers on computational efforts. The value $\omega$ denotes the relaxation parameter of the Krylov subspace method. The order of the system of linear algebraic equations is 40824.

	Number of Iteration
	$\omega$ = 1.00			$\omega$ = 1.58
f/GHz
Structure	10	50	100	10	50	100
no PML	63	72	127	45	53	91
z-PML	649	647	716	431	452	543
yz-PML	13912	27924	32298	16457	44824	104642
xyz-PML	12307	44723	213358	15983	111965	> 10⁶
xyz-PML
(nonov.)	628	591	742	493	436	624

References:

K. BEILENHOFF, W. HEINRICH, H.L. HARTNAGEL, Improved finite-difference formulation in frequency domain for three-dimensional scattering problems, IEEE Transactions on Microwave Theory and Techniques, 40 (1992), pp. 540-546.
A. CHRIST, H.L. HARTNAGEL, Three-dimensional finite-difference method for the analysis of microwave-device embedding, IEEE Transactions on Microwave Theory and Techniques, 35 (1987), pp. 688-696.
G. HEBERMEHL, R. SCHLUNDT, H. ZSCHEILE, W. HEINRICH, Improved numerical methods for the simulation of microwave circuits, Surveys Math. Indust., 9 (1999), pp. 117-129.
G. HEBERMEHL, F.-K. HÜBNER, R. SCHLUNDT, TH. TISCHLER, H. ZSCHEILE, W. HEINRICH, Simulation of microwave and semiconductor laser structures including absorbing boundary conditions, in: Challenges in Scientific Computing - CISC2002, E. Bänsch, ed., vol. 35 of Lecture Notes Comput. Sci. Eng., Springer, Berlin, 2003, pp. 131-159.
, Eigen mode computation of microwave and laser structures including PML, in: Scientific Computing in Electrical Engineering, W.H.A. Schilders, S.H.M.J. Houben, E.J.W. ter Maten, eds., Mathematics in Industry, Springer, 2004, pp. 196-205.
G. HEBERMEHL, J. SCHEFTER, R. SCHLUNDT, TH. TISCHLER, H. ZSCHEILE, W. HEINRICH, Simulation of microwave circuits and laser structures including PML by means of FIT, Advances in Radio Science, 2 (2004), pp. 107-112.
, Simulation of microwave and semiconductor laser structures including PML: Computation of the eigen mode problem, the boundary value problem, and the scattering matrix, WIAS Preprint no. 987, 2004 .
R. SCHLUNDT, G. HEBERMEHL, F.-K. HÜBNER, W. HEINRICH, H. ZSCHEILE, Iterative solution of systems of linear equations in microwave circuits using a block quasi-minimal residual algorithm, in: Scientific Computing in Electrical Engineering, U. van Rienen, M. Günther, D. Hecht, eds., vol. 18 of Lecture Notes Comput. Sci. Eng., Springer, Berlin, 2001, pp. 325-333.
T. WEILAND, A discretization method for the solution of Maxwell's equations for six-component fields, Electronics and Communication (AEÜ), 31 (1977), pp. 116-120.