Process simulation in gas turbine engineering

[Next]:

Three-dimensional conforming Delaunay mesh generation

[Up]:

Projects

[Previous]:

Simulation of microwave and semiconductor laser

[Contents]

[Index]

Process simulation in gas turbine engineering

Collaborator: J. Borchardt, F. Grund, D. Horn

Cooperation with: D. Zeitz (ALSTOM (Switzerland) Ltd., Baden)

Supported by: ALSTOM (Switzerland) Ltd., Baden

Description:

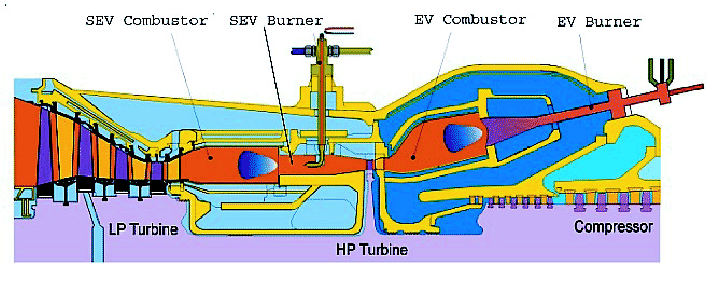
In today's gas turbine engineering, it is not only needed to increase the capacity and the efficiency of the turbines, but also to reach the highest possible reliability and to ensure a safe, economic, and environmentally acceptable operation of heavy duty industrial turbines. In modern gas-fired combined-cycle power stations, a new generation of advanced gas turbines (Figure 1) is used. These turbines use the sequential combustion technology. With this technology, the fuel is injected twice into the gas turbine, and the capacity and efficiency are increased without increasing the fire temperature. Power augmentation can be achieved, among other things, by inlet cooling and high fogging. The processes which proceed within these turbines are highly integrated, leading to complex and highly nonlinear process models. In this context, large-scale process simulation problems may arise. Using concentrated physical models, high-dimensional systems of nonlinear or differential-algebraic equations (DAEs) have to be solved in steady state or dynamic process simulation, respectively. For their solution, robust, fast, and reliable numerical simulation tools are needed.

**Fig. 1:** Gas turbine for power stations (source: www.power.alstom.com)
$\ProjektEPSbildNocap{0.8\textwidth}{turbine3.eps}$

To handle those large-scale process simulation problems, we have developed a simulation approach that is based on ``divide and conquer'' techniques. Within this approach, the modular structure of the process is exploited for an efficient numerical solution of the resulting equation system. Because the modular process structure corresponds to the hierarchical unit structure of the underlying plant, the corresponding system of equations can be structured into subsystems according to the units. Based on this structure, it can then be portioned into blocks

F_j(t, Y_j(t), $\displaystyle \dot{{Y}}_{j}^{}$ (t), U_j(t), $\displaystyle \dot{{U}}_{j}^{}$ (t), u(t)) = 0, j = 1(1)p,

F_j : $\displaystyle \mathbb {R}$ x $\displaystyle \mathbb {R}$ ^m_j x $\displaystyle \mathbb {R}$ ^m_j x $\displaystyle \mathbb {R}$ ^n-m_j x $\displaystyle \mathbb {R}$ ^n-m_j x $\displaystyle \mathbb {R}$ ^q $\displaystyle \rightarrow$ $\displaystyle \mathbb {R}$ ^m_j, $\displaystyle \sum_{{i=1}}^{{p}}$ m_j = n, t $\displaystyle \in$ [t₀, t_end],

where the vectors Y_j(t) and U_j(t) denote the unknown and coupling variables of the blocks, respectively, and u(t) the parameter functions. In the steady state case, the system of DAEs degenerates to a block-structured system of nonlinear equations. To exploit the hierarchical subsystem structure of the equation system during its numerical solution, we have considerably modified and adapted the standard methods BDF, Newton, and sparse Gaussian elimination. At the other hand, we have appropriately extended the block-partitioned system of equations, so that the approach can be efficiently parallelized on shared memory computers. Within this parallel approach, the equation blocks can be treated almost concurrently, both in the model evaluation as well as in the solution. The key part of parallelization is realized within so-called block-structured Newton-type methods, [1]. Among other things, these methods enable a controlled relaxation decoupling between blocks.

The approach has been implemented in the Block Oriented Process simulator BOP [2] that uses an own compiler to generate a hierarchically structured data interface from a process description with its modeling language MLPE (Modeling Language for Process Engineering).

In the period under report, we have continued our cooperation with ALSTOM (Switzerland) Ltd., a leading gas turbine producer. We have delivered BOP Version 2.0 to ALSTOM, where the simulator is now used for the process simulation of industrial gas turbines. It runs under the Windows XP operating system on PCs, where it is called by ALSTOMs graphical user interface ALPEG. Compared to the previous version, Version 2.0 of BOP contains a number of new features. Among other things, it enables a binary input/output and a direct data transfer between the Java GUI and the simulator via the Java Native Interface (JNI) and a dynamic link library. The scope of the process description possibilities has been considerably extended. The combination ALPEG-BOP is now in successful business use. Different versions of this simulation tool can be used by process designers or sells managers, respectively.

In continuation of this work and based on a new license agreement with ALSTOM, we have started the development of BOP Version 2.1. In this context, we have made changes to the control strategy of the steady state solver within BOP to improve its reliability and performance even in critical regions of the modeling, as, e.g., for the problem of anti-icing and the problem of discontinuous modeling with respect to the turbine operation at low part-load. Competitive simulation runs for those critical problems have shown that BOP still converges where the Aspen Custom Modeler^TM (ACM), a worldwide leading commercial simulation tool of Aspen Technology (USA), fails.

Additionally, we continued the implementation of advanced elements of the modeling language of ACM, whose functionality goes far beyond the scope of MLPE. With it, we have considerably enlarged the application area of BOP. These achievements will finally make it possible to use BOP for the simulation of processes described with the modeling language of ACM, without the necessity to make extensive changes in the process description. The realized language extension covers in particular complex IF-statements which can contain multiple instructions as well as procedure calls, the usage of different actions if a variable is fixed or free, the possibility of defining a new model by extending or modifying an existing one, and the possibility to include source code from a library. Beside this, new standard functions have been implemented and it is now possible to use integer, string, and logical parameters as well as global parameter-type definitions. All these new language elements can now be treated by our three-step compiler, which first analyzes the process description statements, then links the entire system, and finally generates the data and the program interface to the BOP solver. Their practicability has been tested for process descriptions of different industrial gas turbines.

Finally, we have written a documentation [2] for BOP.

For the near future it is planned to add a Monte Carlo simulation mode to the simulator BOP. It should enable probabilistic statements about the process, as, e.g., probability curves for engine power, engine efficiency, or engine exhaust energy.

References:

J. BORCHARDT, Newton-type decomposition methods in large-scale dynamic process simulation, Computers and Chemical Engineering, 25 (2001), pp. 951-961.
J. BORCHARDT, D. HORN, Process Simulator BOP (Version 2.0) -- Documentation, WIAS, Berlin, 2004, pp. 1-74.
, The block oriented process simulator BOP, submitted.
F. GRUND, K. EHRHARDT, J. BORCHARDT, D. HORN, Heterogeneous dynamic process flowsheet simulation of chemical plants, in: Mathematics -- Key Technology for the Future. Joint Projects Between Universities and Industry, W. Jäger, H.J. Krebs, eds., Springer, Berlin, 2003, pp. 184-193.