Mode-locking and Q-switching in semiconductor lasers

[Next]:

Numerical methods for laser dynamics

[Up]:

Projects

[Previous]:

Laser systems with feedback or coupling

[Contents]

[Index]

Subsections

Mode-locking and Q-switching in semiconductor lasers with saturable absorber

Collaborator: D. Rachinskii, M. Radziunas, V. Tronciu, A. Vladimirov

Cooperation with: R. Kaiser, B. Hüttl, C. Kindel (Fraunhofer-Institut für Nachrichtentechnik, Heinrich-Hertz-Institut (HHI), Berlin), D. Turaev (Ben Gurion University, Beer Sheva, Israel), G. Kozyreff, M. Nizette (Free University of Brussels, Belgium), M. Yamada (Kanazawa University, Japan), R.A. Abram (University of Durham, UK), T. Kawakami, S. Ito, T. Ohno, M. Taneya (Sharp Corporation, Tenri, Japan), J. Mørk, K. Yvind (Research Center COM, Technical University of Denmark)

Supported by: Terabit Optics Berlin: project ``Modeling and simulation of mode-locked semiconductor lasers'' (together with Research Group 1)

Description:

Semiconductor lasers operating in mode-locking (ML) regime are efficient, compact, low-cost sources of short optical pulses with high repetition rates (tens and hundreds of GHz), suitable for applications in telecommunication technology. Similarly to other types of lasers, these lasers can be passively mode-locked by incorporating an intracavity saturable absorber section into the laser.

**Fig. 1:** Left: Schematic view of monolithic mode-locked semiconductor laser. Right: QSW ML - domain of Q-switched mode-locking. ML - stable fundamental mode-locking regime. Solid lines - analytical results. Dots - numerical results.
$\makeatletter \@ZweiProjektbilderNocap[h]{0.4\textwidth}{fig2_a1.eps}{fig2_a2.eps} \makeatother$

After the development of a new model for passive ML---a set of differential equations with time delay, [1, 2]---we have obtained a simple and efficient method to analyze the stability of ML pulses and their bifurcations. Reducing the delay differential model to a map that describes the transformation of the ML pulse parameters after one round trip in the cavity, one can study bifurcations of this map, [3, 4]. The continuous-wave (CW) ML regimes correspond to nontrivial fixed points of this map. In this way, we have described the stability domains and bifurcations of ML regimes in monolithic semiconductor lasers. Some of the results are shown in Figure 1.

It is well known that lasers with a saturable absorber have a tendency to exhibit undamped Q-switching (QSW) pulsations. In a mode-locked laser, QSW instability leads to a transition from CW-ML regime to a so-called Q-switched ML regime. It is characterized by a pulse amplitude modulated by the QSW oscillations frequency, which is typically of the order of a few GHz, for semiconductor lasers. Since fluctuations of the ML pulse amplitude are undesirable in most applications, it is an important question how to avoid this type of instability in real devices.

Using the approaches described above, we have suggested analytical approximations for the QSW instability boundary of the fundamental ML regime, [4]. We have studied the dependence of this boundary on several laser parameters and compared it with the results of direct numerical analysis of the original delay differential model (see Figure 1). The results are in good agreement with the experimental data and with the results of direct numerical simulations using the traveling wave model (see Figure 2).

Mode-locking pulsations in the TW model.

Mode-locked pulsations in semiconductor lasers with saturable absorber can also be recovered by the traveling wave (TW) model. Additionally to the delay differential equations (DDE) model discussed above, this model includes the effects of the linear configuration as well as spatial hole burning of carriers, nonlinear gain compression, and spontaneous emission. After adjusting the parameters, the model equations were integrated numerically by our software LDSL-tool over some transient time. The sampling of the computed pulse trains and the corresponding RF-spectra [8] allow to distinguish different operating regimes of the laser and to characterize the quality of the pulses. By repeating this for different values of the control parameters, we can characterize the dynamical behavior of the laser in the parameter space (see Figure 2).

**Fig. 2:** Mode-locked pulsations in current injection / unsaturated loss (voltage) plane.
Left: Signal-to-noise ratio. Right: Pulse width.
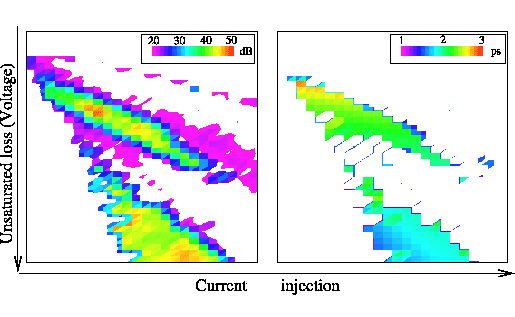$\ProjektEPSbildNocap{0.6\textwidth}{fig2_mr_1.eps}$

Q-switching pulsations in a blue semiconductor laser.

Blue-violet semiconductor lasers are very attractive for high-density optical storage applications. In particular, laser diodes operating at 400 nm are required for CD or DVD systems to increase the disk storage capacity up to 25 Gbytes. A number of other applications, such as full color electroluminescent displays, laser printers, and many others in biology and medicine have increased the interest in such lasers. Recently, specific interest has been focused on the Q-switching operation of blue-emitting devices [5-7]. QSW can significantly increase the laser performance for certain applications and is considered, for example, to be important for the reduction of feedback noise. Figure 3 shows the structure of the InGaN laser (lasing wavelength 395 nm) with saturable absorber that has been investigated. To model the laser properties, we used the Yamada model adapted to the specific case of the InGaN laser with saturable absorber incorporated as a layer parallel to the active region. The region of QSW in the plane of cavity length vs. injected current parameters is shown in Figure 3. As the cavity length is increased, the Q-switching range becomes wider. However, this spread is accompanied by a shift of the threshold current to higher values. Figure 3 also shows quite good agreement between the experimental data (dotted lines terminated by symbols) and the regions of QSW predicted by numerical calculation. Finally, two different possibilities to obtain excitable behavior of the blue laser with saturable absorber have been discussed.

**Fig. 3:** Left: Schematic view of a blue InGaN laser. Right: Numerical (blue line) and experimental (dotted lines) regions of Q-switching. Red line - threshold current.
$\makeatletter \@ZweiProjektbilderNocap[h]{0.4\textwidth}{fig2_t1.eps}{fig2_t2.eps} \makeatother$

References:

A.G. VLADIMIROV, D. TURAEV, G. KOZYREFF, Delay differential equations for mode-locked semiconductor lasers, Opt. Lett., 29 (2004), pp. 1221-1223.
A.G. VLADIMIROV, D. TURAEV, A new model for a mode-locked semiconductor laser, to appear in: Radiophysics and Quantum Electronics, 47 (2004).
, Passive mode-locking with slow saturable absorber: A delay differential model, WIAS Preprint no. 947 , 2004.
D. RACHINSKII, A.G. VLADIMIROV, Q-switching instability in a mode-locked semiconductor laser, WIAS Preprint no. 975 , 2004.
V.Z. TRONCIU, M. YAMADA, R.A. ABRAM, Analysis of the dynamics of a blue-violet InGaN laser with a saturable absorber, Phys. Rev. E, 70 (2004), 026604.
V.Z. TRONCIU, M. YAMADA, T. KAWAKAMI, S. ITO, T. OHNO, M. TANEYA, R.A. ABRAM, A theoretical and experimental investigation of the dynamics of tandem blue-violet lasers, Opt. Commun., 235 (2004), pp. 409-414.
V.Z. TRONCIU, M. YAMADA, R.A. ABRAM, T. KAWAKAMI, S. ITO, T. OHNO, M. TANEYA, Self-pulsation and excitability of blue-violet InGaN lasers, WIAS Preprint no. 940 , 2004.
M. RADZIUNAS Sampling techniques applicable for the characterization of the quality of self pulsations in semiconductor lasers, WIAS Technical Report no. 2, 2002.