[Next]:

Mode-locking and Q-switching in semiconductor lasers

[Up]:

Projects

[Previous]:

Projects

 [Contents] 

 [Index] 

Dynamics and synchronization for laser systems with feedback or coupling

Collaborator: M. Radziunas, K.R. Schneider, V. Tronciu, M. Wolfrum, S. Yanchuk

Cooperation with: L. Recke (Institut für Mathematik, Humboldt-Universität zu Berlin (HU)), A. Samoilenko (Institute of Mathematics, National Academy of Sciences of Ukraine, Kiev), H.-J. Wünsche (Institut für Physik, Humboldt-Universität zu Berlin (HU)) T. Kapitaniak and A. Stefanski (Technical University of Lodz, Poland)

Supported by: DFG: Collaborative Research Centre ``Complex Nonlinear Processes'' (SFB 555), DFG Research Center MATHEON, project D8

Description:

It is well known that in various experimental situations where semiconductor lasers interact by coupling or feedback, they tend to develop instabilities and complicated dynamical behavior on a time scale of GHz. A qualitative and quantitative understanding of such dynamical effects is essential for the development of optoelectronic components in modern telecommunications systems. Using methods from the theory of dynamical systems, one can effectively study and describe such dynamical features.

The performed research in this field was focused to the following topics:

• Feedback lasers with large delay time;
• Systems of coupled lasers and synchronization;
• Entrainment of the modulation frequency.

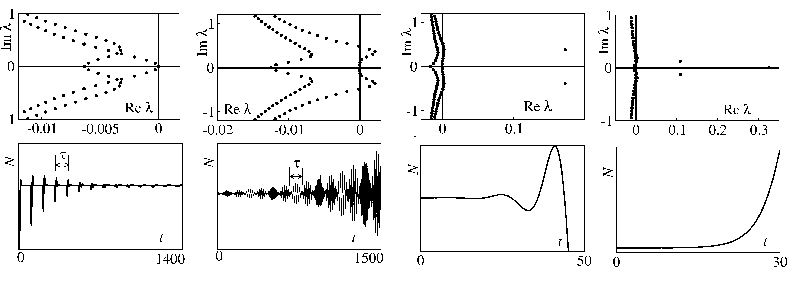
For delay differential equations (DDE) with large delay time we were able to develop a new theoretical approach, using multiple-scale methods, to investigate the eigenvalue problem for stationary and periodic solutions, [3, 4]. In particular, the set of eigenvalues can be splitted into two parts. The first part corresponds to instantaneous instabilities and can be found as zeros of some polynomials. The other set is organized in branches and accounts for contributions from delayed feedback.

Applying this method to the Lang-Kobayashi model for lasers with delayed feedback, we were able to classify the occurring instabilities (see Figure 1): weak stability (first column), weak modulational instability (second column), and strong instability (the last two columns).

Fig. 1: Different types of local (in-)stability for laser with large feedback. Top: Eigenvalues with largest real parts. Bottom: Typical orbit in the vicinity of the corresponding stationary state.

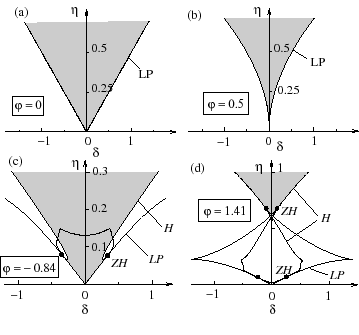
In [6,7], we investigate the synchronization properties of a system of two optically face-to-face coupled lasers. In particular, we observe a highly sensitive dependence of the locking regions and the bifurcation scenario on the coupling phase parameter $\varphi$ (see Figure 2)

Fig. 2: Bifurcations and locking regions (gray) for two coupled lasers. H - Hopf and
LP - saddle-node bifurcation lines. ZH - zero-Hopf bifurcation point.

In [5], we contribute to the development of the general theory of synchronization of coupled systems of the form

$$\dot{x}_{j}^{}$$ = f (x_j) + $$\sum_{{j=1}}^{{n}}$$D_ij(x_j - x_i), x_j $$\in$$ R^k.

We have shown how the synchronization threshold can be estimated for chaotic systems which are coupled via all components by an arbitrary coupling structure.

A classical problem in the theory of synchronization is the problem of frequency entrainment of an oscillatory system by an external force. We were able to extend a result from [9], showing how an entrainment of the modulation frequency can take place even for different wave frequencies, if the frequencies of the carrier wave are sufficiently fast with respect to the modulation. This is an essential feature of pulsating lasers locking to an external optical signal with optical frequency different to that of the laser.

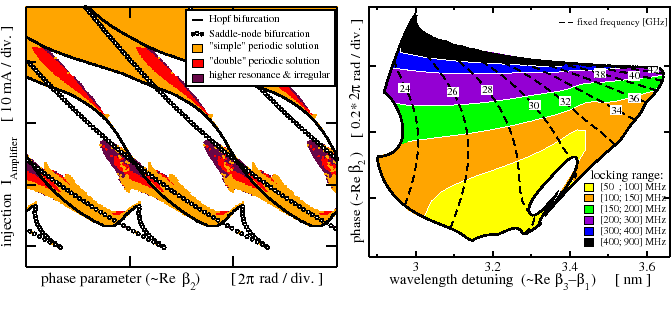
Using the software LDSL-tool, we have analyzed the performance of several types of devices which are developed and produced at the Heinrich Hertz Institute (HHI) as components for optical telecommunications systems. In particular, we have considered a phase-controlled mode-beating (PhaseCOMB) laser consisting of two active sections and a passive section in between and an active feedback laser (AFL) where a single laser section is followed by a passive section for phase tuning and an active amplifier section, [2].

Fig. 3: Using LDSL-tool for investigation of laser structures from HHI.
Left: AFL. Right: Electrically modulated PhaseCOMB.

References:

1. S. BAUER, O. BROX, J. KREISSL, B. SARTORIUS, M. RADZIUNAS, J. SIEBER, H.-J. WÜNSCHE, F. HENNEBERGER, Nonlinear dynamics of semiconductor lasers with active optical feedback, WIAS Preprint no. 866 , 2003, Phys. Rev. E, 69 (2004), 016206.

2. N. KORNEYEV, M. RADZIUNAS, H.-J. WÜNSCHE, F. HENNEBERGER, Mutually injecting semiconductor lasers: Simulations for short and zero delay, in: Proceedings of SPIE: Semiconductor Lasers and Laser Dynamics Conference ``Photonics Europe'', Strasbourg, France, April 26-30, vol. 5452, SPIE, Washington, USA, 2004, pp. 63-70.
3. S. YANCHUK, M. WOLFRUM, Instabilities of stationary states in lasers with long-delay optical feedback, WIAS Preprint no. 962, 2004.
4. S. YANCHUK, Properties of stationary states of delay equations with large delay and applications to laser dynamics, WIAS Preprint no. 944, 2004.
5. A. STEFANSKI, J. WOJEWODA, T. KAPITANIAK, S. YANCHUK, Simple estimation of synchronization threshold in ensembles of diffusively coupled chaotic systems, Phys. Rev. E, 70 (2004), 026217.
6. S. YANCHUK, K.R. SCHNEIDER, L. RECKE, Dynamics of two mutually coupled semiconductor lasers: Instantaneous coupling limit, Phys. Rev. E, 69 (2004), 056221.

7.          , Dynamics of two F2F coupled lasers: Instantaneous coupling limit, in: Proceeding of SPIE: Semiconductor Lasers and Laser Dynamics Conference ``Photonics Europe'', Strasbourg, France, April 26-30, vol. 5452, SPIE, Washington, USA, 2004, pp. 51-62.

8. M. RADZIUNAS, Numerical bifurcation analysis of traveling wave model of multisection semiconductor lasers, WIAS Preprint no. 985 , 2004.

9. L. RECKE, D. PETERHOF, Abstract forced symmetry breaking and forced frequency locking of modulated waves, J. Differential Equations, 144 (1998), pp. 233-262.

[Next]:

Mode-locking and Q-switching in semiconductor lasers

[Up]:

Projects

[Previous]:

Projects

 [Contents] 

 [Index]