Numerical methods for laser dynamics

[Next]:

Periodic processes

[Up]:

Projects

[Previous]:

Mode-locking and Q-switching in semiconductor lasers

[Contents]

[Index]

Numerical methods for laser dynamics

Collaborator: M. Radziunas, A. Vladimirov

Cooperation with: H.-J. Wünsche (Institut für Physik, Humboldt-Universität zu Berlin), J. Sieber (University of Bristol, UK), L. Recke, M. Lichtner (Institut für Mathematik, Humboldt-Universität zu Berlin), B. Sartorius, S. Bauer, U. Troppenz (Fraunhofer-Institut für Nachrichtentechnik, Heinrich-Hertz-Institut, Berlin), H. Wenzel (Ferdinand-Braun-Institut für Höchstfrequenztechnik, Berlin)

Supported by: DFG Reseach Center MATHEON, project D8

Description:

Our software LDSL-tool is a comprehensive toolkit to simulate and to analyze the spatio-temporal dynamical behavior of a broad range of edge-emitting multisection semiconductor lasers, including lasers with dispersive or amplified feedback, mode-locked lasers with saturable absorbers, ring lasers, and the interaction of several lasing sections. It is based on the traveling wave (TW) model

$\displaystyle {\frac{{\partial}}{{\partial t}}}$ E(z, t)	=	H $\displaystyle \left(\vphantom{\partial_z,\beta(z)+\tilde{\beta}(n,\varepsilon \vert E\vert^2,z),z}\right.$ $\displaystyle \partial_{z}^{}$ , $\displaystyle \beta$ (z) + $\displaystyle \tilde{{\beta}}$ (n, $\displaystyle \varepsilon$ \| E\|², z), z $\displaystyle \left.\vphantom{\partial_z,\beta(z)+\tilde{\beta}(n,\varepsilon \vert E\vert^2,z),z}\right)$ I>E(z, t),	E(z, t) $\displaystyle \in$ $\displaystyle \IC^{4}_{}$ ,
$\displaystyle {\frac{{d}}{{d t}}}$ n(z, t)	=	I(z, t) - R(n, z) - $\displaystyle \Re$ e $\displaystyle \langle$ E, G(n, $\displaystyle \varepsilon$ \| E\|², z)E $\displaystyle \rangle$ ,	n(z, t) $\displaystyle \in$ $\displaystyle \IR$ ,

(1)

supplied with reflectivity / transmission / injection conditions for the field E at the edges of each part of the device. Well-posedness and smoothness properties for different types of the TW model have been investigated in [3, 6].

In order to obtain information about different dynamical effects and their sensitive dependence on the various design and control parameters in an efficient way, the further development of LDSL-tool has been focused on the combination of the existing tools for simulations and spectral analysis [4] with the path-following software AUTO [1] for numerical bifurcation analysis. In the case of the TW model, the application of such techniques is based on an effective central manifold reduction, [6], leading to a low-dimensional mode approximation (MA) system of ODEs.

**Fig. 1:** Bifurcations of periodic solutions for a laser with two active sections.
Left: One parameter. Right: Two parameters.
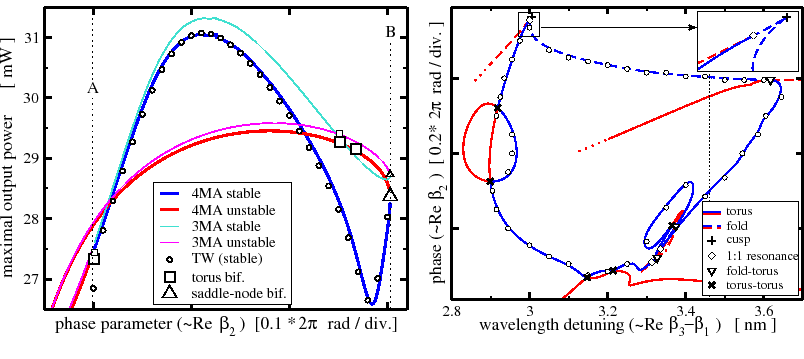$\ProjektEPSbildNocap{0.9\textwidth}{fig2_mr_3.eps}$

Figure 1 shows the result of a numerical bifurcation analysis for a laser with two active sections after reduction to mode approximation (MA) systems, [5]. Empty bullets, obtained by integration of the full TW model, show the good precision for MA systems with sufficiently high dimension.

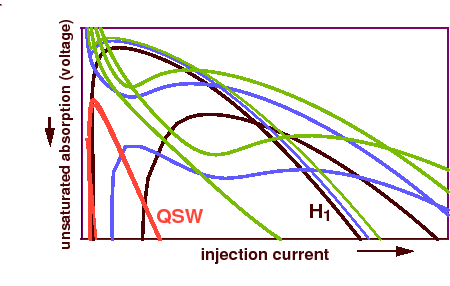
For a numerical bifurcation analysis of the delay differential model for mode-locking in monolithic semiconductor lasers, we have used also the software package DDE-BIFTOOL [2]. Using this package, we have calculated Hopf bifurcations of continuous-wave (CW) solutions (laser modes) of the laser equations and analyzed bifurcations of the solutions with periodic laser intensity. These bifurcate from the CW solutions at Hopf bifurcations and correspond to mode-locking regimes with different repetition rates. An example of a bifurcation diagram is shown in Figure 2.

**Fig. 2:** Curves of Hopf bifurcations for CW solutions of a mode-locked laser.
QSW: Q-switching. H₁: Hopf bifurcations to fundamental mode-locked solution regime.
$\ProjektEPSbildNocap{0.5\textwidth}{fig2_av_4.eps}$

References:

E.J. DOEDEL, A.R. CHAMPNEYS, T.F. FAIRGRIEVE, YU.A. KUZNETSOV, B. SANDSTEDE, X. WANG, AUTO97: Continuation and bifurcation software for ordinary differential equations (with HomCont), Technical Report, Concordia University, Montreal, Canada, 1997.
K. ENGELBORGHS, T. LUZYANINA, G. SAMAEY, DDE-BIFTOOL V. 2.00: A Matlab package for bifurcation analysis of delay differential equations, Technical Report TW-330, Department of Computer Science, Catholic University of Leuven, 2001.
M. LICHTNER, M. RADZIUNAS, Well posedness and smooth dependence for a semilinear hyperbolic system with nonsmooth data, Preprint no. 174 of DFG Research Center MATHEON, Berlin, 2004.
M. RADZIUNAS, H.-J. WÜNSCHE, Multisection lasers: Longitudinal modes and their dynamics, WIAS Preprint no. 939 , 2004, in: ``Optoelectronic Devices - Advanced Simulation and Analysis'', J. Piprek, ed., Springer Verlag, New York, 2005, pp. 121-150, ISBN: 0-387-22659-1.
M. RADZIUNAS, Numerical bifurcation analysis of traveling wave model of multisection semiconductor lasers, WIAS Preprint no. 985 , 2004.
J. SIEBER, M. RADZIUNAS, K.R. SCHNEIDER, Dynamics of multisection semiconductor lasers, Math. Model. Anal., 9 (2004), pp. 51-66.