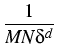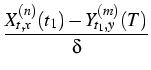Subsections
Applied mathematical finance
Collaborator:
D. Belomestny,
S. Jaschke,
A. Kolodko,
D. Mercurio,
G.N. Milstein,
O. Reiß,
J. Schoenmakers,
V. Spokoiny,
J.-H. Zacharias-Langhans
Cooperation with: C. Byrne (Springer, Heidelberg),
R. Cont (Ecole Polytechnique, Palaiseau, France),
B. Coffey (Merrill Lynch, London, UK),
H. Föllmer, W. Härdle, U. Küchler, R. Stehle (Humboldt-Universität
(HU) zu Berlin),
H. Friebel (Finaris, Frankfurt am Main),
P. Glasserman (Columbia University, New York, USA),
H. Haaf, U. Wystup (Commerzbank AG, Frankfurt am Main),
A.W. Heemink, E.v.d. Berg, D. Spivakovskaya
(Technical University Delft, The Netherlands),
F. Jamshidian (NIB Capital Den Haag, The Netherlands),
J. Kampen (Ruprecht-Karls-Universität, Heidelberg)
J. Kienitz (Postbank, Bonn),
P. Kloeden (Johann Wolfgang Goethe-Universität Frankfurt am Main),
C. März, D. Dunuschat, T. Sauder,
S. Wernicke (Bankgesellschaft Berlin AG, Berlin),
B. Matzack (Kreditanstalt für Wiederaufbau (KfW), Frankfurt am Main),
S. Nair (Chapman & Hall, London, UK),
M. Schweizer (Universität München / ETH Zürich),
S. Schwalm (Reuters FS, Paris, France),
G. Stahl (Bundesaufsichtsamt für das Kreditwesen (BAFin) Bonn),
D. Tasche (Deutsche Bundesbank, Frankfurt am Main)
Supported by:
BMBF: ``Effiziente Methoden zur Bestimmung von Risikomaßen''
(Efficient methods for valuation of risk measures),
DFG: DFG-Forschungszentrum ``Mathematik für Schlüsseltechnologien''
(Research Center ``Mathematics for Key Technologies''), project E5;
SFB 373 ``Quantifikation und Simulation ökonomischer Prozesse''
(Quantification and simulation of economic processes),
Reuters Financial Software, Paris
Description:
The central theme of the project Applied mathematical finance
is the quantitative treatment of problems raised by the financial
industry, based on innovative methods and algorithms
developed in accordance with fundamental principles of mathematical
finance. These problems include
stochastic modeling of
financial data, valuation of complex
derivative instruments (options), and
risk analysis.
The methods and algorithms
developed benefit strongly from the synergy with the projects
Statistical data analysis and Numerical methods for
stochastic models.
(D. Belomestny, A. Kolodko, G.N. Milstein, O. Reiß,
J. Schoenmakers).
The valuation of financial derivatives based
on arbitrage-free asset pricing involves non-trivial
mathematical problems
in martingale theory, stochastic differential equations, and partial
differential equations.
While its main
principles
are established (Harrison, Pliska, 1981), many numerical problems remain
such as the numerical valuation of (multidimensional)
American equity options
and the valuation of Bermudan-style
derivatives involving the term
structure of interest rates (LIBOR models), [6].
The valuation and optimal exercise of American and Bermudan derivatives
is one of the
most important problems both in theory and practice, see, e.g.,
[1].
American options are options contingent on a set of underlyings
which can be exercised at any time in some prespecified future
time interval, whereas Bermudan options may be exercised
at a prespecified discrete set of future exercise dates.
In general, the fair price of an American- or Bermudan-style derivative
can be represented as the solution of an optimal stopping problem.
- American options: For the multidimensional
American option in a generalized Black-Scholes framework,
this optimal stopping problem can be converted into a free boundary
value problem (Stefan problem). In this context we have developed
in [22]
a pure Monte Carlo algorithm for determining the (free) exercise
boundary of an American option.
Due to the thus constructed exercise boundary, the
option may be priced and hedged by well-known Monte Carlo
simulation of a respective Cauchy boundary value problem.
As such we have a pure Monte Carlo procedure for the solution
of a Stefan problem which may be considered remarkable.
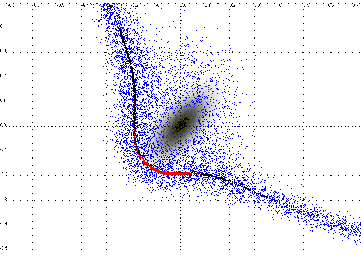
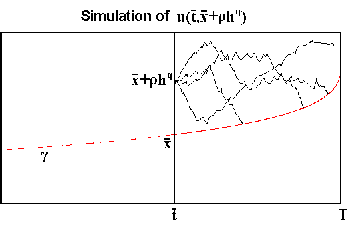
For one dimension the main idea is as follows.
Let us suppose that
the exercise curve x = g'(t) is known from
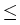 t
t 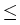 T. By using the free boundary
conditions and taking boundary limits of the Black-Scholes
PDE and its time derivative in the continuation region,
we have shown that the derivative
g'(
T. By using the free boundary
conditions and taking boundary limits of the Black-Scholes
PDE and its time derivative in the continuation region,
we have shown that the derivative
g'(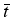 )
can be expressed in
uxxx(
)
can be expressed in
uxxx(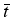 , g'(
, g'(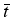 ) +) and
known quantities
ux(
) +) and
known quantities
ux(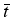 , g'(
, g'(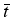 ) +),
uxx(
) +),
uxx(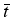 , g'(
, g'(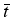 ) +)
which can be expressed in the PDE coefficients and the pay-off function
f. As a result we may compute numerically the third derivative uxxx
via a Taylor expansion by an accurate enough computation of
u(
) +)
which can be expressed in the PDE coefficients and the pay-off function
f. As a result we may compute numerically the third derivative uxxx
via a Taylor expansion by an accurate enough computation of
u(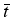 ,
,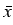 +
+ 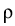 hq)
in a neighborhood point in the continuation region. The latter
can be done by standard Monte Carlo simulation using the
known exercise curve for
hq)
in a neighborhood point in the continuation region. The latter
can be done by standard Monte Carlo simulation using the
known exercise curve for
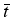
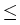 t
t 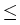 T, see Figure 1.
Having
g'(
T, see Figure 1.
Having
g'(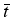 ), the exercise curve can be extended one step,
g(
), the exercise curve can be extended one step,
g(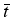 - h)
- h) 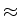 g(
g(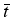 ) - g'(
) - g'(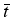 )h, and then we proceed
in the same way. In [22] this method is generalized to the
multidimensional case.
)h, and then we proceed
in the same way. In [22] this method is generalized to the
multidimensional case.
Fig. 1:
Backward construction of the exercise
boundary in one dimension
 |
- American options in time-delayed models: In [10] we have
started to consider optimal stopping rules for models driven by
stochastic delay differential equations. A natural application is
the valuation of American options where the volatility depends on
the past. For instance the choice
postulates that the volatility is driven by the deviation of the
current price from an exponentially weighted average over the
past, which is close in spirit to classical chart techniques.
In certain particular cases the models can be described by higher
dimensional Markov diffusion processes with singular diffusion
matrix. We study the singular free boundary value problem
occurring in the analytical description of the solution.
- Bermudan-style products: For Bermudan options we have
constructed in [18] an efficient Monte Carlo
method for computing a price upper bound. The method
is based on a duality approach for Monte Carlo construction
of a Bermudan price upper bound via the Doob-Meyer
martingale part of an approximation of the respective
Snell envelope process, [15], [36].
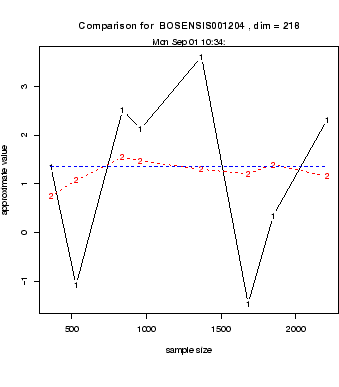
In our approach we enclose the theoretical upper bound by approximating from
above with an ``up-up'' estimator due to Haugh & Kogan
and from below by a newly developed lower estimator,
called ``up-low'' estimator.
Both the ``up-up'' estimator and the ``up-low'' estimator require
in general simulations in simulations and, as a consequence,
tend to be time-consuming.
However, we show that
by taking a suitable convex combination of the lower and upper
estimator we can obtain a combined estimator
which requires only a very low number of inner simulations and, as a
result, this estimator has a higher computational efficiency.
For an application to the Bermudan swaption, approximated by the
maximum of ``still alive'' swaptions, see Figure 2,
and for more details, see [18].
Fig. 2:
Bias of different estimators
as function of K inner simulations. The dashed line is the
combined estimator
 |
Another new method for
constructing
an upper bound of the Bermudan/American price using
some lower bound is currently
in development. This approach
is based on the fact that an American option is equivalent to a
European option with a consumption process involved.
The value of the upper
bound V(t, x) at a position (t, x) is constructed by the Monte Carlo
method.
Our attention focuses on constructing new numerical
procedures and their practical implementation.
The results of numerical
experiments confirm efficiency of the algorithms
proposed ([3]).
In an initiated research cooperation with J. Kampen at Heidelberg University, we aim
to value Bermudan-style derivatives
in the LIBOR market model based on higher
order approximation of Greenian kernels. The Greenian kernels
are connected with the
(high-dimensional) LIBOR process and
integration with respect to these kernels will be implemented on sparse grids.
- Monte Carlo evaluation of Greeks by finite differences:
In many cases the price of an option can be represented as the solution of a
Cauchy boundary value problem for a parabolic PDE. As a consequence, option
prices can be computed by Monte Carlo simulation of a respective
system of stochastic differential equations. Derivatives of the solution,
in financial terms called ``Greeks'', can in principal
be computed by finite differences of solutions obtained by Monte Carlo
simulation. In [26] it is shown that this method is effective
when in the Monte Carlo simulation the method of dependent realizations
is exploited. An error analysis is given, and numerical experiments are
in agreement with the developed theory. A related
Monte Carlo method for computation of Greeks was previously constructed
in [23], see also [35].
(O. Reiß, J. Schoenmakers).
Robust calibration of the LIBOR market model, a
popular benchmark model for effective forward interest rates
([5], [17], [28]),
to liquidly traded instruments
such as caps and swaptions has been a challenging problem
for several years. In particular, calibration methods which avoid
the use of historical data are very desirable, both from a practical
and a more fundamental point of view. The dynamics of the LIBOR model is
given by
dLi = - 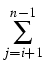 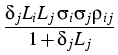 dt + Li dt + Li 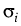 dW(n)i, dW(n)i,
|
(1) |
where the LIBOR/EurIBOR processes Li are defined in
[t0, Ti],
with
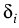 = Ti+1 - Ti being day count fractions
and
= Ti+1 - Ti being day count fractions
and 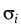 being scalar deterministic volatility
functions. Further,
(W(n)i(t) | t0
being scalar deterministic volatility
functions. Further,
(W(n)i(t) | t0 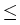 t
t 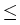 Tn-1) are correlated
Wiener processes under the so-called terminal measure
Tn-1) are correlated
Wiener processes under the so-called terminal measure
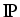 n,
with deterministic local covariance structure
n,
with deterministic local covariance structure
<
dW(n)i,
dW(n)j > =
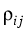 dt
dt.
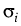 (t) (t) |
: = |
cig(Ti - t) |
|
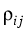 (t) (t) |
: = |
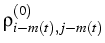 , m(t) : = min{m : Tm , m(t) : = min{m : Tm 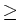 t}, t}, |
|
with a simple parametric function
g(s) : = g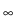 + (1 - g
+ (1 - g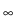 + as)exp(- bs),
and, for example, one of the correlation structures
developed by Schoenmakers & Coffey in [40], [41],
based on some semi-parametric framework, [19], [39].
+ as)exp(- bs),
and, for example, one of the correlation structures
developed by Schoenmakers & Coffey in [40], [41],
based on some semi-parametric framework, [19], [39].
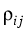 |
= |
exp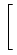 - - 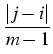 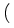 -ln -ln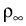 + + |
|
| |
|
  + + 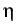 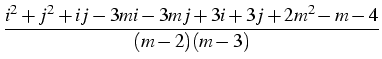 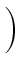 ![$\displaystyle \left.\vphantom{\left.+\eta\frac{i^2+j^2+ij-3mi-3mj+3i+3j+2m^2-m-4}{(m-2)(m-3)}
\right)}\right]$](img596.gif) , , |
|
| |
|
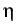 > 0, 0 < > 0, 0 < 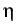 < - ln < - ln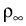 . . |
|
The thus designed volatility structure relies on sensible assumptions
regarding the behavior of forward rates and implies a kind of
time shift invariance when
ci 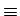 c. Calibration of this volatility
structure to a set of market cap and swaption volatilities comes down to
fit the model cap and swaption volatilities to a rather flat surface
of market quotes, see the first picture in Figure 3.
c. Calibration of this volatility
structure to a set of market cap and swaption volatilities comes down to
fit the model cap and swaption volatilities to a rather flat surface
of market quotes, see the first picture in Figure 3.
The LIBOR model is in a sense designed to price cap(let)s
in closed form. Indeed, for any function g and correlation structure
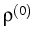 ,
caps can be matched perfectly by appropriate
choice of the coefficients ci. However, since caps are in fact one period
swaptions, the model swaption volatility surface intersects with
the market volatility surface at the 1 period
swaption line, regardless of
the choice of g and
,
caps can be matched perfectly by appropriate
choice of the coefficients ci. However, since caps are in fact one period
swaptions, the model swaption volatility surface intersects with
the market volatility surface at the 1 period
swaption line, regardless of
the choice of g and
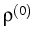 .
See the second picture in Figure 3
for a model swapvol surface for some rather
arbitrary choice of g and
.
See the second picture in Figure 3
for a model swapvol surface for some rather
arbitrary choice of g and
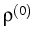 . This is in fact
an intrinsic stability
problem (see also [37]), since basically two explaining powers are available determining
one rotation angle. We have resolved this problem by introducing
economically motivated regularizations of the least squares object function
and implemented the so developed stable procedures for testing against
market data. Meanwhile our calibration methods are gaining interest,
appearing from consulting requests (Reuters FS, Bankgesellschaft Berlin AG)
and a currently developing book project ([38]).
. This is in fact
an intrinsic stability
problem (see also [37]), since basically two explaining powers are available determining
one rotation angle. We have resolved this problem by introducing
economically motivated regularizations of the least squares object function
and implemented the so developed stable procedures for testing against
market data. Meanwhile our calibration methods are gaining interest,
appearing from consulting requests (Reuters FS, Bankgesellschaft Berlin AG)
and a currently developing book project ([38]).
Fig. 3:
Market swaption vols and model vols for some typical but
arbitrary choice of
g,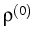
![\makeatletter
\@ZweiProjektbilderNocap[h]{7cm}{MSV.eps}{g1R1.eps}
\makeatother](img598.gif) |
(D. Mercurio,
V. Spokoiny).
In cooperation with the project Statistical data analysis,
new techniques for the volatility estimation for
financial time series have been developed, [12], [21],
[30].
- Locally time-homogeneous volatility estimation:
The usual approach to volatility estimation starts
from the definition of a parametric model,
such as GARCH, and then fits this model to the data,
globally, for example, by maximum likelihood
estimation. On the other hand, practitioners usually
prefer to focus on the most recent data,
which are perceived as more informative. Therefore,
exponentially weighted moving average
and window estimators are often applied in practice.
However, the results of these techniques
strongly depend on the choice of the smoothing
parameters.
The attempt of the technique proposed in [21] is
precisely to put the window estimator on a sound
statistical basis. The most
recent window of data on which the
estimation is performed is selected through a multiple
testing procedure, where the
probability of rejecting a homogeneous interval is
specified. Applications to
exchange rate data show good results.
The method is successfully applied to problems of volatility
forecasting and Value at Risk evaluation.
Fig. 4:
Returns and estimated
volatility for the JPY/USD exchange rate
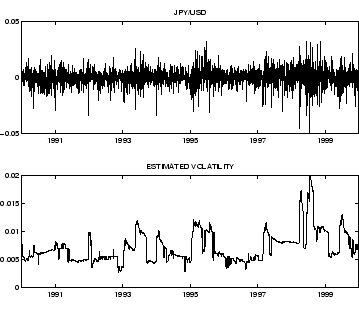 |
- Volatility estimation from discrete observations:
Since many artifacts are observed in high-frequency or tick data during
the day, one often uses daily data in historical financial time
series to draw inference on the underlying model parameters. In
mathematical finance the underlying models are, however, usually
formulated in continuous time. Nevertheless, classical methods for
estimating the volatility in diffusion-type models are only
asymptotically consistent for observation distances tending to
zero. In [12] and [30],
we studied the prototype problem of
estimating the drift and diffusion (volatility) coefficient in a
scalar diffusion X from the observation
(Xn
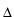 )0
)0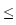 n
n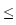 N for arbitrary
N for arbitrary 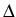 > 0. We prove optimality of our
nonparametric estimation method in a minimax sense for fixed
> 0. We prove optimality of our
nonparametric estimation method in a minimax sense for fixed
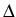 > 0 and the asymptotics
N
> 0 and the asymptotics
N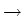
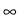 . First simulation
results indicate that already for relatively small observation
distances
. First simulation
results indicate that already for relatively small observation
distances 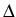 our method outperforms classical procedures
based on quadratic variation estimation.
our method outperforms classical procedures
based on quadratic variation estimation.
(S. Jaschke, D. Mercurio, O. Reiß,
J. Schoenmakers, V. Spokoiny, J.-H. Zacharias-Langhans).
Since the Basel Committee's proposal for ``An internal model-based approach to
market risk capital requirements'' (1995) was implemented in national laws,
banks have been allowed to use internal models for estimating their market
risk and have been able to compete in the innovation of risk management
methodology. Since all banks are required to hold adequate capital reserves
with regard to their outstanding risks, there has been a tremendous demand for
risk management solutions. A similar ``internal ratings-based approach'' is
planned for the controlling of credit risk in the ``Basel II'' process, which
is due to be implemented in national laws by 2006. Meanwhile, credit
derivatives play an important role as vehicle for banks to transform credit
risk into de jure market risk and to potentially lower the required reserves.
Such problems of risk measurement and risk modeling are the subject of
the research on ``Mathematical methods for risk management''.
This research is supported by the BMBF project ``Efficient methods for
valuation of risk measures'', which continued in 2003 in
cooperation with the Bankgesellschaft Berlin AG.
Problems of both market and credit risk from the
viewpoint of supervisory authorities are being worked on in cooperation with
the BAFin.
Although the basic principles of the
evaluation of market risks are now more or less settled, e.g.,
[2], [8], [9], [29],
in practice
many thorny statistical and numerical issues
remain to be solved.
Specifically the industry standard, the approximation of portfolio risk
by the so-called ``delta-gamma normal'' approach, can be criticized
because of the quadratic loss approximation and the Gaussian assumptions.
Further, in
the context of the ``Basel II'' consultations
fundamental questions arise in the area of Credit Risk Modeling.
(G.N. Milstein,
J. Schoenmakers, V. Spokoiny).
Monte Carlo methods are very important in the field
of applied mathematical finance, and we present here some interesting
applications.
- Forward-reverse simulation of worse case probabilities:
Previously, Milstein, Schoenmakers and Spokoiny ([25])
developed in cooperation with the project Statistical
data analysis a new transition
density estimator for diffusion processes which is basically root-N
consistent for any dimension of the diffusion process. This estimator,
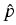 (t, x, T, y) = (t, x, T, y) = 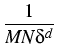 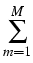 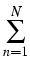 K K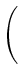 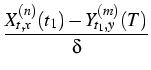 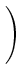 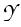 t1, y(m)(T), t1, y(m)(T), |
|
|
(3) |
which does not suffer from the ``curse of dimensionality'',
is based on forward simulation of the given process X and reverse
simulation of an adjoint process
(Y,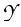 ) which can be constructed
via the (formal) adjoint of the generator of the original process.
For estimating worst-case scenario probability
densities in financial applications it is desirable to have
a variation of the method in [25] for
discrete time models, which have basically more
potential for modeling heavy tails.
To this end we have constructed in [24]
the discrete adjoint process for a large class of discrete
time Markov processes such that the
forward-reverse density estimator (3)
goes through for such processes as well. Several financial applications are
currently studied in cooperation with the project Statistical
data analysis.
) which can be constructed
via the (formal) adjoint of the generator of the original process.
For estimating worst-case scenario probability
densities in financial applications it is desirable to have
a variation of the method in [25] for
discrete time models, which have basically more
potential for modeling heavy tails.
To this end we have constructed in [24]
the discrete adjoint process for a large class of discrete
time Markov processes such that the
forward-reverse density estimator (3)
goes through for such processes as well. Several financial applications are
currently studied in cooperation with the project Statistical
data analysis.
- Variance reduction by Stratification:
In cooperation with the project Numerical methods for
stochastic models we have been considering
the following problem in [20].
Many financial portfolios are influenced by a variety of underlyings, but
which are only locally correlated. The valuation of such products leads to
high-dimensional integration, but the integrands possess a small effective dimension.
Prototypically we exhibit the following situation, describing a
portfolio of a set
{It1, It2,..., Itm},
of m underlyings with respective shares
w1, w2,..., wm, determining
the present value
Vt = 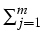 wjItj.
There are many numerical schemes for the valuation of such financial
products. Often a reasonable approximation is obtained using the
wjItj.
There are many numerical schemes for the valuation of such financial
products. Often a reasonable approximation is obtained using the
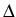 -
- 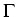 -normal-method for the forecast of Vt+1 at a future time
knowing Vt, given by
-normal-method for the forecast of Vt+1 at a future time
knowing Vt, given by
Vt+1 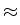 Vt + Vt + 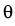 + + 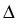 y + y + 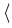 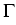 y, y y, y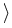 , ,
|
(4) |
with
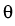 ,
,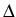 , and
, and 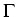 completely determined by the structure of the
portfolio, and y Gaussian innovations,
see [11]. In this case we obtain a quadratic functional in the
underlyings. This remains quadratic when turning to the independent risk
factors. Normally,
completely determined by the structure of the
portfolio, and y Gaussian innovations,
see [11]. In this case we obtain a quadratic functional in the
underlyings. This remains quadratic when turning to the independent risk
factors. Normally, 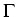 is sparse.
is sparse.
In this situation, the ANOVA decomposition of the integrand in (4)
admits only up to bivariate contributions, such that it makes sense to apply
Monte Carlo methods, which intrinsically use this information. For the
situation at hand, we propose the use of
randomized orthogonal arrays
of strength 2 ([4]),
which are known to show super-convergence, i.e.
converge faster than usual Monte Carlo.
Test calculations based on real-world data provided by the Bankgesellschaft Berlin AG actually show superiority above conventional
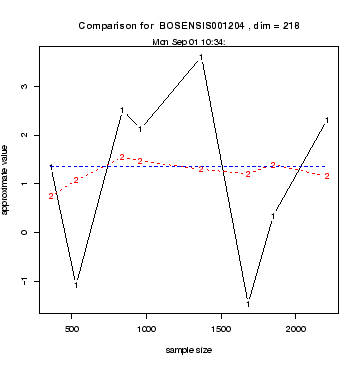
simulations, see Figure 6.
Fig. 6:
Convergence Monte-Carlo (1) vs. orthogonal arrays (2)
 |
References:
- F. AITSAHLIA, P. CARR,
American options: A comparison of numerical methods,
in: Numerical Methods in Finance,
L.C.G. Rogers, D. Talay, eds.,
Cambridge University Press, 1997, pp. 67-87.
- P. ARTZNER, F. DELBAEN, J.M. EBER, D. HEATH,
Coherent measures of risk,
Math. Finance, 9 (1998), pp. 203-228.
- D. BELOMESTNY, G.N. MILSTEIN,
Monte Carlo evaluation of American options using consumption
processes, working paper, 2003.
-
R.C. BOSE, A. BUSH,
Orthogonal arrays of strength two and three,
Ann. Math. Statistics, 23 (1952), pp. 508-524.
-
A. BRACE, D. GATAREK, M. MUSIELA,
The market model of interest rate dynamics,
Math. Finance, 7 (1997), pp. 127-155.
- M. BROADIE, J. DETEMPLE,
Recent advances in numerical methods for pricing
derivative securities,
in: Numerical Methods in Finance,
L.C.G. Rogers, D. Talay, eds.,
Cambridge University Press, 1997, pp. 43-66.
- CREDIT SUISSE FIRST BOSTON,
CreditRisk+ : A Credit Risk Management Framework,
available at http://www.csfb.com/creditrisk,
1997.
- P. EMBRECHTS, C. KLÜPPELBERG, T. MIKOSCH,
Modelling Extremal Events,
Springer, Berlin, 1997.
- J. FRANKE, W. HÄRDLE, G. STAHL,
Measuring Risk in Complex Stochastic Systems,
Lect. Notes Stat., vol. 147, Springer, New York, 2000.
-
P. GAPEEV, M. REISS, A note on optimal
stopping in models with delay, Discussion Paper no. 47 of
Sonderforschungsbereich 373, Humboldt-Universität zu Berlin, 2003.
-
P. GLASSERMAN,
Monte Carlo Methods in Financial Engineering, Springer, Berlin, 2003.
-
E. GOBET, M. HOFFMANN, M. REISS,
Nonparametric estimation of scalar diffusions based on low
frequency data, to appear in: Ann. Statist.
- H. HAAF, O. REISS, J.G.M. SCHOENMAKERS,
Numerically stable computation of CreditRisk+,
WIAS Preprint no. 846, 2003, to apper in: Journal of Risk.
-
A. HAMEL, Risikomaße und ihre Anwendungen, to
appear as Report of Martin-Luther-Universität Halle-Wittenberg.
- M.B. HAUGH, L. KOGAN, Pricing American options: A duality
approach, working paper 2001, to appear in: Oper. Res.
- W. HÄRDLE, H. HERWARTZ, V. SPOKOINY,
Time inhomogeneous multiple volatility modelling,
Discussion Papers of Interdisciplinary Research no. 7,
Humboldt-Universität zu Berlin, SFB 373,
2001.
- F. JAMSHIDIAN,
LIBOR and swap market models and measures,
Finance Stoch., 1 (1997), pp. 293-330.
- A. KOLODKO, J.G.M. SCHOENMAKERS,
An efficient dual Monte Carlo upper bound for Bermudan-style
derivatives, WIAS Preprint no. 877, 2003.
-
O. KURBANMURADOV, K.K. SABELFELD, J.G.M. SCHOENMAKERS,
Lognormal approximations to LIBOR market models,
J. Comput. Finance, 6 (2002), pp. 69-100.
- P. MATHÉ,
Using orthogonal arrays to valuate
 -
- 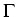 -normal,
working paper, 2003.
-normal,
working paper, 2003.
- D. MERCURIO, V. SPOKOINY,
Estimation of time dependent volatility via local
change point analysis,
WIAS Preprint no 904, 2004.
-
G.N. MILSTEIN, O. REISS, J.G.M. SCHOENMAKERS,
A new Monte Carlo method for American options,
earlier version: WIAS Preprint no. 850, 2003,
to appear in: Int. J. Theor. Appl. Finance.
-
G.N. MILSTEIN, J.G.M. SCHOENMAKERS,
Monte Carlo construction of hedging strategies against
multi-asset European claims,
Stochastics Stochastics Rep., 73 (2002), pp. 125-157.
- G.N. MILSTEIN, J.G.M. SCHOENMAKERS, V. SPOKOINY,
Forward-reverse representations for Markov chains,
working paper, 2003.
- ,
Transition density estimation for stochastic differential
equations via forward-reverse representations,
WIAS Preprint no. 680, 2001, to appear in: Bernoulli.
- G.N. MILSTEIN, M.V. TRETYAKOV,
Numerical analysis of Monte Carlo finite difference evaluation of Greeks,
WIAS Preprint no. 808, 2003.
- ,
Simulation of a space-time bounded diffusion,
Ann. Appl. Probab., 9 (1999), pp. 732-779.
- K.R. MILTERSEN, K. SANDMANN, D. SONDERMANN,
Closed-form solutions for term structure derivatives with
lognormal interest rates,
J. Finance, 52 (1997), pp. 409-430.
- R.B. NELSON,
An Introduction to Copulas,
Springer, New York, 1999.
-
M. REISS, Nonparametric volatility
estimation on the real line from low-frequency observations, 2003,
submitted.
- O. REISS, Dependent sectors and an extension to incorporate
market risk, to appear in: CreditRisk+ in the Banking Industry,
M. Gundlach, F. Lehrbass, eds., Springer, Berlin Heidelberg, 2004.
- ,
Fourier inversion algorithms for generalized
CreditRisk+ models and an extension to
incorporate market risk, WIAS Preprint no. 817, 2003.
- ,
Fourier inversion techniques for CreditRisk+, in:
CreditRisk+ in the Banking Industry, F. Lehrbass, M. Gundlach,
eds., Springer, Berlin Heidelberg, 2004.
- ,
Mathematical methods for the efficient assessment
of market and credit risk,
Ph.D. thesis, Universität Kaiserslautern,
2003,
available at http://kluedo.ub.uni-kl.de/volltexte/2003/1621.
- O. REISS, U. WYSTUP,
Computing option price sensitivities using homogeneity
and other tricks,
in: Foreign Exchange Risk: Models, Instruments
and Strategies, Risk Books, London, 2002,
pp. 127-142, and The Journal of Derivatives, 9 (2001),
pp. 41-53.
- L.C.G. ROGERS,
Monte Carlo valuation of American options,
Math. Finance, 12 (2002), pp. 271-286.
- J.G.M. SCHOENMAKERS,
Calibration of LIBOR models to caps and swaptions:
A way around intrinsic instabilities via
parsimonious structures and a collateral market criterion,
WIAS Preprint no. 740, 2002.
- ,
Robust Libor Modelling and Pricing of Derivatives Products,
in preparation.
- J.G.M. SCHOENMAKERS, B. COFFEY,
LIBOR rate models, related derivatives and model calibration,
WIAS Preprint no. 480, 1999.
- ,
Stable implied calibration of a multi-factor LIBOR model via a
semi-parametric correlation structure,
WIAS Preprint no. 611, 2000.
- ,
Systematic generation of parametric correlation structures for the
LIBOR market model,
Int. J. Theor. Appl. Finance, 6 (2003), pp. 507-519.
- D. TASCHE,
Capital allocation with CreditRisk+, to appear in: CreditRisk+
in the Banking Industry, F. Lehrbass, M. Gundlach, eds., Springer,
Berlin Heidelberg, 2004.
LaTeX typesetting by I. Bremer
2004-08-13


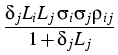 dt + Li
dt + Li 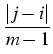
![\makeatletter
\@ZweiProjektbilderNocap[h]{7cm}{MSV.eps}{g1R1.eps}
\makeatother](img598.gif)