Numerical analysis of complex stochastic models

Cooperation with: T. Foken (Universität Bayreuth), N.O. Jensen (Risoe National Laboratory, Denmark), V. Kukharets (Obukhov Institute of Atmospheric Physics, Moscow, Russia), O. Kurbanmuradov (Physical Technical Institute, Turkmenian Academy of Sciences, Ashkhabad), A. Levykin, I. Shalimova, N. Simonov (Institute of Computational Mathematics and Mathematical Geophysics, Russian Academy of Sciences, Novosibirsk), M. Mascagni (Florida State University, Tallahassee, USA), A. Onishuk (Institute of Chemical Kinetics and Combustion, Russian Academy of Sciences, Novosibirsk), O. Smidts (Université Libre de Bruxelles (ULB), Belgium), M.V. Tretyakov (University of Wales, UK), H. Vereecken (Forschungszentrum (FZ) Jülich, Institut für Chemie und Dynamik der Geosphäre), T. Vesala, U. Rannik (Helsinki University, Finland), W. Wagner (WIAS: Research Group 5)

In 2003, the main research was concentrated on the development of new stochastic models, methods, and simulation techniques for solving high-dimensional boundary value problems with random parameters (involving Wiener processes and log-normal random fields). The developed approach was successfully applied to the transport of gases and particles within plant canopies and statistically isotropic porous media, potential and elasticity problems, and to the numerical solution of Smoluchowski equation governing ensembles of diffusing, nucleating, and coagulating particles under free molecular collision regime. A particular case of interactions analyzed is related to stochastic Hamiltonian systems and Langevin-type equations based on symplectic integrators. This approach results in effective numerical methods for stochastic differential equations used in mathematical finance. Remarkably, the constructed stochastic Lagrangian model for porous media appears to be the first one developed while the discussion and different attempts to construct such a model have a long history in the literature. This work is a result of the cooperation with the Jülich Forschungszentrum (H. Vereecken) and the Free University of Brussels (O. Smidts). The results of the research of 2003 have been published in the refereed papers [1], [5], [7], [8], [9], [10], [13], [14], [18], [22], seven WIAS preprints, and presented in eight talks at international conferences.

In 2003, the EU project INTAS-99-1501 has been successfully finished. In this project, seven groups from five countries (Finland, Denmark, Germany, Russia, Turkmenistan) have been working on the development of new measurement instruments for monitoring the gas-aerosol exchange in the plant canopies. The build-up of the measurement technique was coordinated by Professor T. Vesala (Helsinki University), and K.K. Sabelfeld (WIAS) was the scientific coordinator in the simulation models development. A special issue of the journal Boundary-layer Meteorology with papers stemming from this project is to appear in 2004.

The group has organized (Chairman K.K. Sabelfeld) the IVth IMACS Seminar on Monte Carlo Methods (September 15-19, 2003, Berlin) which was co-sponsored by WIAS, the Konrad-Zuse-Zentrum and the DFG. This Seminar is the world's largest international forum on stochastic simulation (see also p.

1. Eulerian and Lagrangian stochastic models for the transport in porous media

The Langevin-type models assume that the trajectory ( $\bf X(t),{\bf V}(t))$ of a particle is governed by a stochastic differential equation of Ito type

dX_i(t)	=	V_i dt,	(1)
dV_i(t)	=	a_i( $\displaystyle \bf X$ (t), $\displaystyle \bf V$ (t), t) dt + $\displaystyle \sigma_{{ij}}^{}$ ( $\displaystyle \bf X$ (t), $\displaystyle \bf V$ (t), t) dB_j(t), i = 1, 2, 3.

The summation convention over the repeated indices is used. Here a_i are the drift, and $\sigma_{{ij}}^{}$ the diffusion terms, and B_j are standard independent Wiener processes.

This kind of models is widely used in atmospheric turbulence simulations (see, e.g., [4], [11], [15]). The motivation comes from the fact that the characteristic time of the acceleration correlations is much less than that for the velocity correlations which is the case for the turbulent flow.

In a porous medium, when dealing with laminar flows we cannot treat the velocity as turbulent. However, the acceleration direction is highly varying because of the pore structure inhomogeneity. Therefore, the acceleration and velocity fields can be considered as random flows, and the Langevin-type equations can be used to describe the Lagrangian dynamics. The main difference, compared to the turbulence, is that the flow in porous media is extremely anisotropic, which results in a much more complicated form of the drift and diffusion terms. In particular, here we do not have this nice and simple diffusion term in the form of a constant C₀ coming from the Kolmogorov theory of fully developed turbulence.

Compared to random displacement models (RDM) ([2], [3]), the Langevin-type models involve more information about the statistics of velocity, e.g., they naturally use the information about the probability density function (pdf) of the Eulerian velocity field. Indeed, in case the velocity is incompressible, it is known that the Eulerian pdf p_E is related to the coefficients of the Langevin equation through the well-mixed condition

$\displaystyle {\frac{{\partial p_E}}{{\partial t}}}$ + u_i $\displaystyle {\frac{{\partial p_E}}{{\partial x_i}}}$ + $\displaystyle {\frac{{\partial}}{{\partial u_i}}}$ (a_ip_E) = $\displaystyle {\frac{{1}}{{2}}}$ $\displaystyle {\frac{{\partial^2 (b_{ij} p_E)}}{{\partial u_i \partial u_j}}}$ ,

(2)

This complicates the model, but wins very important gains: the model is able to describe the transport in detail for scales inside or compared to the Lagrangian time scale where the dispersion is not linear, so generally we deal here with a super-diffusion phenomenon ([17]). It is important that the model enables to evaluate the concentration field not far from the source. Thus, these models are free of the Fickian hypothesis.

The derivation of the drift and diffusion terms is not simple. So far, even in the well-studied atmospheric turbulence, there is no theoretical approach which derives uniquely the expressions for these terms. Therefore, experimental and heuristical information is used to determine the model. In our case we evaluated the diffusion term from the numerical solution of the flow equations. We have derived the drift term and the tensor $\sigma_{{ij}}^{}$ from the well-mixed condition (2), and via the numerical solution of the following boundary value problem with random coefficients

$\displaystyle \bf\nabla$ $\displaystyle \left[\vphantom{ K({\bf r}) {\bf\nabla} \phi({\bf r}) }\right.$ K( $\displaystyle \bf r$ ) $\displaystyle \bf\nabla$ $\displaystyle \phi$ ( $\displaystyle \bf r$ ) $\displaystyle \left.\vphantom{ K({\bf r}) {\bf\nabla} \phi({\bf r}) }\right]$ = 0 , $\displaystyle \bf r$ $\displaystyle \in$ $\displaystyle \cal {D}$

(3)

$\displaystyle \phi$ ( $\displaystyle \bf r$ ) = F_D( $\displaystyle \bf r$ ) , $\displaystyle {\frac{{\partial \phi({\bf r})}}{{\partial n}}}$ = F_N( $\displaystyle \bf r$ ) , $\displaystyle \bf r$ $\displaystyle \in$ $\displaystyle \cal {S}$ _N .

(4)

The hydraulic conductivity K in (3) is a random field, the hydraulic potential $\phi$ ( $\bf r$ ) is therefore also a random field, and the velocity is a random vector field as well.

A validation of the model developed was made through a comparison of various statistical characteristics obtained with our method with those known from measurements and direct numerical simulations. The backward trajectory approach we suggest in [24] for finance models is used here for variance reduction purpose.

Under the assumption of smallness of fluctuations in the hydraulic conductivity we construct a stochastic Eulerian model for the incompressible flow as a divergence-free Gaussian random field with a spectral tensor of a special structure derived from Darcy's law. A randomized spectral representation is then used to simulate this random field. Numerical results are compared with the analytical results obtained by the small perturbation expansion in [2], [3]. A series of test calculations confirmed the high accuracy and computational efficiency of the method. Comparisons with asymptotically exact results show a good agreement.

**Fig. 1:** Samples of specific discharge perturbation random fields q₁, q₂, for the isotropic hydraulic conductivity. Left picture: the correlation length I_Y = 1, right picture: I_Y = 0.5. The number of harmonics was N = 100.
$\makeatletter \@ZweiProjektbilderNocap[h]{7.5cm}{field1.eps}{field2.eps} \makeatother$

**Fig. 2:** A cloud of 5000 particles ejected by an instantaneous point source at the origin, shown at the time instant t' = 30, $\sigma_{Y}^{2}$ = 10^-2 (left picture) and $\sigma_{Y}^{2}$ = 1 (right picture)
$\makeatletter \@ZweiProjektbilderNocap[h]{7.5cm}{fig_8a.eps}{fig_8b.eps} \makeatother$

The samples of the velocity field are constructed by a very fast spectral randomization method ([16]). For illustration, we show here two samples of such a field in Figure 1. The particle scattering by this velocity field is shown in Figure 2.

The work is done in cooperation with ULB, Brussels, and FZ Jülich, Institute of Chemistry and Dynamics of the Geosphere, the results are presented in [8], [10]. The backward trajectory technique developed in our project was also usefully applied by our colleagues in the Statistical data analysis project.

2. Random Walk methods for the iterative solution of high-dimensional boundary value problems

Suppose a homogeneous isotropic medium G with a boundary $\Gamma$ is given, whose state in the absence of body forces is governed by the Lamé equation, see, e.g., [16], [21]:

The first boundary value problem for the Lamé equation consists in finding a vector function $\bf u$ $\in$ C²(G) $\cap$ C( $\bar{G}$ ) satisfying the boundary condition

The stochastic algorithm is based on the spherical mean value relation for the general n-dimensional case, see, e.g., [21].

The regular solutions to the system (5) satisfy the following spherical mean value relation in S(x, r)

u_i(x) = $\displaystyle {\frac{{n}}{{2(n+\alpha )\omega_n}}}$ $\displaystyle \sum\limits_{{j=1}}^{n}$ $\displaystyle \int\limits_{{\Omega}}^{}$ $\displaystyle \Big($ (2 - $\displaystyle \alpha$ ) $\displaystyle \delta_{{ij}}^{}$ + $\displaystyle \alpha$ (n + 2)s_is_j $\displaystyle \Big)$ u_j(x + rs) d $\displaystyle \Omega$ (s),

(7)

Standard Monte Carlo walk on spheres process uses this relation so that the transition in the Markov chain goes from the center of the sphere to its surface ([21]).

We suggest a further development of the method proposed in [23] which is based on a generalization of the spherical mean value relation for an arbitrary point inside the sphere. This generalization is written

It can be shown that the new method converges much faster compared to the standard walk on spheres method. Namely, the cost of the new method is log log(| $\varepsilon$ |)/ $\varepsilon^{2}_{}$ while for the standard method it is log(| $\varepsilon$ |)/ $\varepsilon^{2}_{}$ . Remarkably, the cost is very weakly dependent on n, the dimension of the problem. Different modifications of this approach are discussed in [19], [23], [24].

In a cooperation with the group of Professor M. Mascagni (Florida State University, Tallahassee, USA), the permeability for a complicated geometry of a porous medium is studied to find the distribution of the velocity field. The methods used are the Decentred Random Walk on Spheres (DRWS) suggested by K.K. Sabelfeld and I. Shalimova ([24]). In a cooperation with the Institute of Computational Mathematics and Mathematical Geophysics, Russian Academy of Sciences, Novosibirsk (Dr. I. Shalimova), an additional validation of the model based on the DRWS method is made by applying the Random Walk on Boundary process ([20]).

3. Stochastic particle method for the evaluation of Footprint functions

Forward and backward stochastic Lagrangian trajectory simulation methods are developed to calculate the footprint and cumulative footprint functions of concentration and fluxes in the case when the ground surface has an abrupt change of the roughness height. The statistical characteristics of the stochastic model are extracted numerically from a closure model we developed for the atmospheric boundary layer. The flux footprint function is perturbed in comparison with the footprint function for a surface without change in properties. The perturbation depends on the observation level as well as the roughness change and the distance from the observation point. It is concluded that the footprint function for a horizontally homogeneous surface, widely used in the estimation of sufficient fetch for measurements, can be seriously biased in many cases of practical importance.

Over a horizontally homogeneous surface the flux measured by micrometeorological technique equals to the surface flux. This principle is used to determine the surface exchange by the eddy covariance (EC) technique ([4]). The flux footprint function links the surface emissions to the observed fluxes above surface at EC measurement level. The footprint function is therefore used to estimate a distance required to make reliable EC measurements, i.e. if the horizontal extent of underlying surface of interest is sufficient to determine its exchange rate. Extended tower measurements of fluxes over forests have been used during the last ten years to obtain detailed information on carbon and water exchanges between forest canopies and atmosphere. Large areas of forest, however, are not common in Europe nor in the USA. The footprint models based on analytical diffusion theory as well as Lagrangian stochastic simulation of an ensemble of fluid parcel trajectories assume a horizontally homogeneous surface. For forest canopies the footprint models involve a number of uncertainties originating from the parametrization of the canopy turbulence features. Such models are frequently applied to estimate the contribution of an area of certain upwind distance, or to estimate the fetch to ensure that the given area contributes a certain percent to the observed flux, by vaguely assuming that the footprint function for a horizontally homogeneous surface is a good approximation for a more complex situation with changes in the surface properties. In reality changes in the surface roughness can be very drastic, for example in the case of forest and field interface. Also the thermal inhomogeneities induced by albedo and repartitioning of available energy into sensible and latent heat fluxes can be significant, this will be analyzed, however, in the future work. So we deal here with pure mechanical turbulence caused by the surface roughness.

The governing equations involve the closure model for the mean flow and stochastic differential equations for the Lagrangian trajectories. There exists a variety of closure models for turbulent mixing, ranging from constant eddy coefficient parametrization to detailed Large Eddy Simulations and Direct Numerical Simulation. We assume that the mean profiles in the boundary layer of atmosphere are described by the following system:

u $\displaystyle {\frac{{\partial u}}{{\partial x}}}$ + w $\displaystyle {\frac{{\partial u}}{{\partial z}}}$	=	$\displaystyle {\frac{{\partial }}{{\partial z}}}$ k $\displaystyle {\frac{{\partial u}}{{\partial z}}}$ + f (v - G sin $\displaystyle \alpha$ ),
			(8)
u $\displaystyle {\frac{{\partial v}}{{\partial x}}}$ + w $\displaystyle {\frac{{\partial v}}{{\partial z}}}$	=	$\displaystyle {\frac{{\partial }}{{\partial z}}}$ k $\displaystyle {\frac{{\partial v}}{{\partial z}}}$ - f (u - G cos $\displaystyle \alpha$ )

is the momentum equation, where the Coriolis parameter is given by f = 2 $\Omega$ sin $\varphi$ , $\Omega$ = 7.29 10^-5s^-1, G is the geostrophic wind, and $\varphi$ is the angle between the x-axis and the isobare; $\alpha$ is the angle between the x-axis and the direction of the geostrophic wind. Further,

u $\displaystyle {\frac{{\partial b}}{{\partial x}}}$ + w $\displaystyle {\frac{{\partial b}}{{\partial z}}}$ = $\displaystyle \alpha_{b}^{}$ $\displaystyle {\frac{{\partial }}{{\partial z}}}$ k $\displaystyle {\frac{{\partial b}}{{\partial z}}}$ + k $\displaystyle \left[\vphantom{\Big(\frac {\partial u} {\partial z}\Big)^2 + \Big(\frac {\partial v} {\partial z}\Big)^2}\right.$ $\displaystyle \Big($ $\displaystyle {\frac{{\partial u}}{{\partial z}}}$ $\displaystyle \Big)^{2}_{}$ + $\displaystyle \Big($ $\displaystyle {\frac{{\partial v}}{{\partial z}}}$ $\displaystyle \Big)^{2}_{}$ $\displaystyle \left.\vphantom{\Big(\frac {\partial u} {\partial z}\Big)^2 + \Big(\frac {\partial v} {\partial z}\Big)^2}\right]$ - $\displaystyle \bar{\varepsilon}$ ,

(9)

l = $\displaystyle \Big($ $\displaystyle {\frac{{1}}{{\kappa z}}}$ + $\displaystyle {\frac{{1}}{{l_0}}}$ $\displaystyle \Big)^{{-1}}_{}$ , k = C_kl $\displaystyle \sqrt{{b}}$ ,

(10)

The functions vary in the layer z₀ $\le$ z $\le$ h, h being the height of the boundary layer, and z₀ the roughness height. The system of equations is considered with the following boundary conditions:

u = 0, v = 0, w = 0, at z = z₀,

u = G cos $\displaystyle \alpha$ , v = G sin $\displaystyle \alpha$ at z = h, x $\displaystyle \le$ 0,

$\displaystyle {\frac{{\partial u}}{{\partial z}}}$ = $\displaystyle {\frac{{\partial v}}{{\partial z}}}$ = 0at z = h, x > 0 ,

$\displaystyle {\frac{{\partial b}}{{\partial z}}}$ = 0at z = z₀,and b = 0 at z = h .

We present the backward estimators for the evaluation of footprint functions in the case of the boundary layer with the sources uniformly distributed over the strips D_i, i = 1,..., n_sr. For simplicity, we have taken the x-axis coincident with the direction of the geostrophical wind, i.e. $\alpha$ = 0.

The backward trajectory starts at time t, at the detector point with the velocity sampled from the Eulerian velocity pdf p_E(u, x) which is assumed to be Gaussian. Below, we denote by $\bar{u}_{{Ek}}^{}$ the k-th component (k = 1, 2, 3) of the mean Eulerian velocity vector, and the hat over the symbols x and u is to indicate that this is a finite-difference approximation to the true Lagrangian trajectory.

The backward trajectory simulation is conveniently carried out through the semi-implicit Euler scheme, which can be written for one time step as follows:

$\displaystyle \hat{x}_{k}^{}$ (t - $\displaystyle \Delta$ t) = $\displaystyle \hat{x}_{k}^{}$ (t) - ( $\displaystyle \hat{u}{^\prime}_{k}$ (t) + $\displaystyle \bar{u}_{{Ek}}^{}$ (t, $\displaystyle \hat{x}$ (t)) $\displaystyle \Delta$ t,

$\displaystyle \hat{u}{^\prime}_{k}$ (t - $\displaystyle \Delta$ t) = $\displaystyle \hat{u}{^\prime}_{k}$ (t) - $\displaystyle \hat{a}{^\prime}_{k}$ (t, $\displaystyle \hat{x}$ (t - $\displaystyle \Delta$ t), $\displaystyle \hat{u}$ (t)) $\displaystyle \Delta$ t + $\displaystyle \sqrt{{C_0\bar\varepsilon(t-\Delta t,\hat x(t-\Delta t)) \Delta t}}$ $\displaystyle \eta_{{tk}}^{}$ ,

d $\displaystyle \hat{x}_{k}^{}$	=	( $\displaystyle \hat{u}{^\prime}_{k}$ + $\displaystyle \bar{u}_{{Ek}}^{}$ ) ds ,
d $\displaystyle \hat{u}{^\prime}_{k}$	=	$\displaystyle \hat{a}{^\prime}_{k}$ ds + $\displaystyle \sqrt{{C_0\bar\varepsilon}}$ $\displaystyle \;\stackrel{{\leftarrow}}{{d}}\;$ W_k(s), s < t, k = 1, 2, 3,

Let $\tau_{{ij}}^{}$ be the time at which the trajectory ( $\hat{{\bf x}}$ (s), $\hat{{\bf u}}$ (s)), s $\le$ t, reaches the ground surface and touches the i-th strip: the first touchdown at $\tau_{{i1}}^{}$ , the second (after a reflection from the boundary) at $\tau_{{i2}}^{}$ , etc., and the last one at $\tau_{{iN_i}}^{}$ . The random estimators have the following form, for the concentration,

c_i = $\displaystyle \left\langle\vphantom{ \sum\limits_{j=1}^{N_i} \frac{2}{\Delta_i}\frac{1} {\vert\hat u_3(\tau_{ij})\vert}}\right.$ $\displaystyle \sum\limits_{{j=1}}^{{N_i}}$ $\displaystyle {\frac{{2}}{{\Delta_i}}}$ $\displaystyle {\frac{{1}}{{\vert\hat u_3(\tau_{ij})\vert}}}$ $\displaystyle \left.\vphantom{ \sum\limits_{j=1}^{N_i} \frac{2}{\Delta_i}\frac{1} {\vert\hat u_3(\tau_{ij})\vert}}\right\rangle$ ,

q_iz = $\displaystyle \left\langle\vphantom{ \sum\limits_{j=1}^{N_i}\frac{2}{\Delta_i} \frac{\hat u_3(t)} {\vert\hat u_3(\tau_{ij})\vert}}\right.$ $\displaystyle \sum\limits_{{j=1}}^{{N_i}}$ $\displaystyle {\frac{{2}}{{\Delta_i}}}$ $\displaystyle {\frac{{\hat u_3(t)}}{{\vert\hat u_3(\tau_{ij})\vert}}}$ $\displaystyle \left.\vphantom{ \sum\limits_{j=1}^{N_i}\frac{2}{\Delta_i} \frac{\hat u_3(t)} {\vert\hat u_3(\tau_{ij})\vert}}\right\rangle$ , i = 1,..., n_sr.

Here $\Delta_{i}^{}$ are the widths of the surface strips ejecting the particles, and the angle brackets stand for the averaging over the ensemble of independent backward trajectories.

A sensitivity analysis is made for the footprint functions under perturbation of the roughness height; two cases are considered: (1) smooth-to-rough, and (2) rough-to-smooth change of the roughness height. The calculations show that the footprint function of concentration is more sensitive than that of the vertical flux.

It is concluded that the footprint and cumulative footprint functions of concentration for a horizontally homogeneous surface, widely used in the estimation of sufficient fetch for measurements, can be seriously biased in many cases of practical importance. The calculations show that the footprint area based on the cumulative concentrations, if estimated through the homogeneous case, can be essentially under- or overestimated, compared to the true inhomogeneous case.

The work is done in cooperation with Prof. Dr. T. Vesala and Dr. U. Rannik (Helsinki University, Finland), N.O. Jensen (Risoe National Laboratory, Denmark), V. Kukharets (Obukhov Institute of Atmospheric Physics, Moscow, Russia), O. Kurbanmuradov (Physical Technical Institute, Turkmenian Academy of Sciences, Ashkhabad, A. Levykin (Institute of Computational Mathematics and Mathematical Geophysics, Russian Academy of Sciences, Novosibirsk).

4. New stochastic particle methods for the Smoluchowski coagulation equation: Variance reduction and error analysis

In the stochastic models for the simulation of coagulation equation it is well known that the decrease of the number of particles in a model system is the main source of the variance increase ([6]). To overcome it, H. Babovsky has suggested to transform the standard Smoluchowski equation (governing the particle concentration) to the mass-flow equation

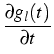$\displaystyle {\frac{{\partial g_l(t)}}{{\partial t}}}$ = $\displaystyle \sum\limits_{{i=1}}^{{l-1}}$ $\displaystyle {\frac{{1}}{{i}}}$ K_i(l-i)g_ig_l-i - g_l $\displaystyle \sum\limits_{{i\geq 1}}^{}$ $\displaystyle {\frac{{1}}{{i}}}$ K_lig_i, l $\displaystyle \geq$ 1;whereg_l(t) = lu_l(t).

However, the distribution of small and large particles in mass-flow systems is still far from being uniform. In fact, even in the case of constant coagulation coefficients K_ij = 1 the decrease of particle concentration with the growth of size l (for any fixed time t) is exponential:

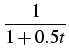
u_l(t) = (1 + 0.5t)^-2 $\displaystyle \left(\vphantom{1-\frac{1}{1+0.5t}}\right.$ 1 - $\displaystyle {\frac{{1}}{{1+0.5t}}}$ $\displaystyle \left.\vphantom{1-\frac{1}{1+0.5t}}\right)^{{l-1}}_{}$ .

Therefore, it is reasonable to introduce a weight function w(l ) increasing with the growth of l, and to transform the original Smoluchowski equation to a ``weight equation'' for the new variable, the weighted concentration z_l(t) = w(l )u_l(t). This weight equation reads obviously

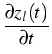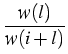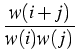$\displaystyle {\frac{{\partial z_l(t)}}{{\partial t}}}$ = $\displaystyle {\frac{{1}}{{2}}}$ $\displaystyle \sum\limits_{{i+j=l}}^{}$ $\displaystyle \hat{{K}}_{{ij}}^{}$ z_iz_j - z_l $\displaystyle \sum\limits_{{i\geq 1}}^{}$ $\displaystyle \hat{{K}}_{{li}}^{}$ $\displaystyle {\frac{{w(l)}}{{w(i+l)}}}$ z_i, l $\displaystyle \geq$ 1; $\displaystyle \hat{{K}}_{{ij}}^{}$ = K_ij $\displaystyle {\frac{{w(i+j)}}{{w(i)w(j)}}}$ .

To solve this equation, we develop a generalization of the method of fictitious jumps (MFJ). Together with this algorithm, we construct a generalization of the method of majorant frequencies (MMF). Though the latter algorithm can be treated as the particular case of the former, it is very important itself.

We apply the method developed to simulate a coagulation-evaporation process of aerosol particles in free molecule collision regime.

Consider a coagulation-evaporation process in a free molecule regime, which is governed by the equation

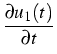		$\displaystyle {\frac{{\partial u_1(t)}}{{\partial t}}}$ = - u₁ $\displaystyle \sum\limits_{{i\geq 1}}^{}$ K_i1u_i + $\displaystyle \sum\limits_{{i\geq 3}}^{}$ E_iu_i +2E₂u₂,

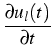		$\displaystyle {\frac{{\partial u_l(t)}}{{\partial t}}}$ = $\displaystyle {\frac{{1}}{{2}}}$ $\displaystyle \sum\limits_{{i+j=l}}^{}$ K_iju_iu_j - u_l $\displaystyle \sum\limits_{{i\geq 1}}^{}$ K_liu_i - E_lu_l + E_l+1u_l+1, l $\displaystyle \geq$ 2

K_ij = $\displaystyle \left(\vphantom{\frac{3}{4\pi}}\right.$ $\displaystyle {\frac{{3}}{{4\pi}}}$ $\displaystyle \left.\vphantom{\frac{3}{4\pi}}\right)^{{\frac{1}{6}}}_{}$ $\displaystyle \left(\vphantom{\frac{6kT}{\rho_p}}\right.$ $\displaystyle {\frac{{6kT}}{{\rho_p}}}$ $\displaystyle \left.\vphantom{\frac{6kT}{\rho_p}}\right)^{{\frac{1}{2}}}_{}$ $\displaystyle \left(\vphantom{\frac{1}{i}+\frac{1}{j}}\right.$ $\displaystyle {\frac{{1}}{{i}}}$ + $\displaystyle {\frac{{1}}{{j}}}$ $\displaystyle \left.\vphantom{\frac{1}{i}+\frac{1}{j}}\right)^{{\frac{1}{2}}}_{}$ $\displaystyle \left(\vphantom{i^{\frac{1}{3}}+j^{\frac{1}{3}}}\right.$ i + j $\displaystyle \left.\vphantom{i^{\frac{1}{3}}+j^{\frac{1}{3}}}\right)^{2}_{}$ ;

E_j = EK_1jexp $\displaystyle \left(\vphantom{A\left(j^{\frac{2}{3}}-(j-1)^{\frac{2}{3}}\right)}\right.$ A $\displaystyle \left(\vphantom{j^{\frac{2}{3}}-(j-1)^{\frac{2}{3}}}\right.$ j - (j - 1) $\displaystyle \left.\vphantom{j^{\frac{2}{3}}-(j-1)^{\frac{2}{3}}}\right)$ $\displaystyle \left.\vphantom{A\left(j^{\frac{2}{3}}-(j-1)^{\frac{2}{3}}\right)}\right)$ .

The question we are interested in is how the values of the evaporation parameters influence the behavior of the process, in particular, we study the total concentration of all particles whose sizes are larger than a given size j_*: c_{j_*}(t) = $\displaystyle \sum\limits_{{i\geq j_*}}^{}$ u_i(t).

The work is done in cooperation with W. Wagner (WIAS, Research Group 5) and A. Onishuk (Institute of Chemical Kinetics and Combustion, Russian Academy of Sciences, Novosibirsk).

5. A probabilistic approach to the solution of complicated problems of mathematical physics

The numerical evaluation of Wiener integrals is an important and difficult task. Many approaches are proposed for solving this problem. As a rule, the known numerical methods reduce a path integral to a high-dimensional integral which is then approximated using either conventional deterministic or Monte Carlo methods. The high dimension of these integrals makes the calculations of the Wiener integrals extremely difficult.

We developed a numerical integration of stochastic differential equations together with the Monte Carlo technique to evaluate conditional Wiener integrals of exponential-type functionals. An explicit Runge-Kutta method of order four and implicit Runge-Kutta methods of order two were constructed. The corresponding convergence theorems are proved. To reduce the Monte Carlo error, a variance reduction technique is considered. The effectiveness of the constructed algorithms allowed us to evaluate the conditional Wiener integrals for a large dimension. Results of numerical experiments are in good agreement with the theory.

Nonlinear PDEs are mostly investigated by numerical methods, which are traditionally based on deterministic approaches. In [1] we propose an approximation method based on a probabilistic approach for the three-dimensional system of Navier-Stokes equations with spatial periodic boundary conditions. The method exploits the ideas of weak-sense numerical integration of stochastic differential equations. Despite the probabilistic nature, this method is nevertheless deterministic. The probabilistic approach takes into account a coefficient dependence on the space variables and a relationship between diffusion and advection in an intrinsic manner. In particular, the derived method allows us to avoid difficulties stemming from highly varying coefficients and strong advection.

Numerical methods for stochastic Hamiltonian systems and Langevin-type equations based on symplectic integrators were further developed with an analysis of stability problems of stochastic dynamics.

In [13], [14], specific methods for stochastic Hamiltonian systems and Langevin-type equations are proposed. Stochastic Hamiltonian systems, like deterministic Hamiltonian systems, possess the property of preserving symplectic structure (symplecticness). A lot of attention in deterministic numerical analysis has been paid to the symplectic integration of Hamiltonian systems. This interest is motivated by the fact that symplectic integrators in comparison with usual numerical schemes allow us to simulate Hamiltonian systems for very long time intervals with high accuracy. Symplectic methods for stochastic Hamiltonian systems proposed in [13] have significant advantages over standard schemes for SDEs as well.

It is natural to expect that making use of numerical methods, which are close, in a sense, to symplectic ones, also has some advantages when applying them to stochastic systems close to Hamiltonian ones. An important and fairly large class of such systems is the Langevin-type equations. The Langevin-type equations have a widespread occurrence in models from physics, chemistry, and biology. In [14] we construct special numerical methods which preserve some specific properties of the Langevin-type equations. The proposed methods are such that they degenerate to symplectic methods when the system degenerates to a Hamiltonian one, and their law of phase volume contractivity is close to the exact one. The presented numerical tests of both symplectic and quasi-symplectic methods clearly demonstrate superiority of the proposed methods for very long time intervals in comparison with existing standard methods. Different examples of stochastic differential equations used in mathematical finance are now analyzed by this approach to find an optimal numerical method with small variance.