Subsections
Collaborator:
D. Belomestny,
V. Essaoulova,
A. Hutt,
P. Mathé,
D. Mercurio,
H.-J. Mucha,
J. Polzehl,
V. Spokoiny
Cooperation with:
F. Baumgart (Leibniz-Institut für Neurobiologie, Magdeburg), R. Brüggemann, Ch. Heyn, U. Simon (Institut für Gewässerökologie und Binnenfischerei, Berlin), P. Bühlmann, A. McNeil (ETH Zürich, Switzerland), C. Butucea (Université Paris 10, France), M.-Y. Cheng (National Taiwan University, Taipeh), A. Daffertshofer (Free University of Amsterdam, The Netherlands), A. Dalalyan (Université Paris 6, France), J. Dolata (Johann Wolfgang Goethe-Universität Frankfurt am Main), L. Dümbgen (University of Bern, Switzerland), J. Fan (Princeton University, USA), J. Franke (Universität Kaiserslautern), R. Friedrich (Universität Münster), F. Godtliebsen (University of Tromsø, Norway), H. Goebl, E. Haimerl (Universität Salzburg), A. Goldenshluger (University of Haifa, Israel), I. Grama (Université de Bretagne-Sud, Vannes, France), J. Horowitz (Northwestern University, Chicago, USA), B. Ittermann (Physikalisch-Technische Bundesanstalt (PTB), Berlin), A. Juditsky (Université de Grenoble, France), I. Molchanov (University of Bern, Switzerland), K.-R. Müller (Fraunhofer FIRST, Berlin), M. Munk (Max-Planck-Institut für Hirnforschung, Frankfurt am Main), S.V. Pereverzev (RICAM, Linz, Austria), H. Riedel (Universität Oldenburg), B. Röhl-Kuhn (Bundesanstalt für Materialforschung und -prüfung (BAM), Berlin), R. von Sachs (Université Catholique de Louvain, Belgium), A. Samarov (Massachusetts Institute of Technology, Cambridge, USA), M. Schrauf (DaimlerChrysler, Stuttgart), S. Sperlich (University Carlos III, Madrid, Spain), U. Steinmetz (Max-Planck-Institut für Mathematik in den
Naturwissenschaften, Leipzig), P. Thiesen (Universität der Bundeswehr, Hamburg), G. Torheim (Amersham Health, Oslo, Norway), C. Vial (ENSAI, Rennes, France), Y. Xia (National University of Singapore, Singapore), S. Zwanzig (Uppsala University, Sweden)
Supported by:
DFG: DFG-Forschungszentrum ``Mathematik für Schlüsseltechnologien''
(Research Center ``Mathematics for Key Technologies''), project A3;
SFB 373 ``Quantifikation und Simulation Ökonomischer Prozesse''
(Quantification and simulation of economic processes),
Humboldt-Universität zu Berlin;
Priority Program 1114 ``Mathematische Methoden der Zeitreihenanalyse und
digitalen Bildverarbeitung'' (Mathematical methods for time series analysis and
digital image processing)
Description:
The project Statistical data analysis focuses on the
development, theoretical investigation and application of modern
nonparametric statistical methods, designed to model and analyze
complex data structures. WIAS has, with main mathematical
contributions, obtained authority for this field, including its
applications to problems in technology, medicine, and environmental
research as well as risk evaluation for financial products.
Methods developed in the institute within this project area
can be grouped into the following main classes.
(D. Belomestny, V. Essaoulova,
A. Hutt, D. Mercurio, H.-J. Mucha, J. Polzehl, V. Spokoiny).
The investigation and development of adaptive smoothing methods have
been driven by interesting problems from imaging and time series
analysis. Applications to imaging include signal detection in
functional Magnet Resonance Imaging (fMRI) and tissue
classification in dynamic Magnet Resonance Imaging (dMRI)
experiments, image denoising, analysis of images containing
Poisson counts or binary information or the analysis of Positron
Emission Tomography (PET) data.
Our approach for time series focuses on locally stationary time
series models. These methods allow for abrupt changes of model
parameters in time. Intended applications for financial time
series include volatility modeling, volatility prediction, and
risk assessment.
The models and procedures proposed and investigated at WIAS are
based on two main approaches, the pointwise
adaptation, originally
proposed in [46] for estimation of regression functions with
discontinuities, and adaptive weights smoothing, proposed in
[33] in the context of image
denoising.
The main idea of the pointwise adaptive approach is to search, in each design point, for the
largest acceptable window that does not contradict to the assumed
local model, and to use the data within this window to obtain
local parameter estimates. This allows for estimates with nearly
minimal variance under controlled bias.
The general concept behind adaptive weights smoothing
is structural
adaptation. The procedure attempts to
recover the unknown local structure from the data in an iterative
way while utilizing the obtained structural information to improve
the quality of estimation. This approach possesses a number of
remarkable properties like preservation of edges and contrasts and
nearly optimal noise reduction inside large homogeneous regions.
It is almost dimension free and is applicable to high-dimensional
situations.
Both ideas have been investigated and applied in a variety of
settings.
- Imaging problems:
The pointwise adaptive approach has been extended
and theoretically investigated for the denoising of 2D images
in [32]. The procedure delivers an optimal (in rate) quality of edge recovering and
demonstrates a reasonable numerical performance.
Adaptive weights smoothing has been generalized to cover
locally smooth images in [36],
see Figure 1 for an example, and local likelihood
estimation for exponential family models in
[35]. The latter allows,
e.g., to handle images containing Poisson counts, binary or
halftone images or images with intensity-dependend gray
value distributions.
Fig. 1:
Reconstruction of a
piecewise smooth image by local polynomial AWS
 |
- Adaptive wavelet thresholding:
Modifications of the AWS procedure have been developed for
denoising one- and two-dimensional data via wavelet
thresholding. The estimates obtained by the AWS procedure turn out
to be spatially adaptive. They attain the near optimal rate of
estimation over Besov classes
Bsp, q. The procedure
performs well in terms of the mean absolute error as well as
visually. The use of AWS for wavelet thresholding allows for improved
compression rates.
Fig. 2:
Reconstruction of an artificial image by wavelet thresholding
using AWS (Compression rate (CR): 0.031), SURE thresholding (CR:
0.188), and the NeighBlock method of Cai and Silverman
([4]) (CR: 0.087)
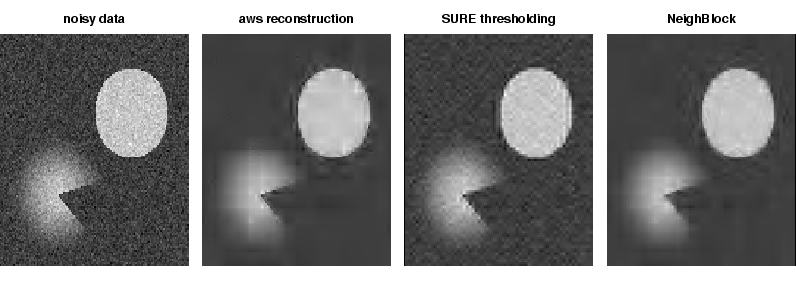 |
.
- Functional and dynamic magnetic resonance
experiments:
Adaptive weights smoothing allows for the analysis of
spatio-temporal structures. The methods proposed in
[34] have been tested on fMRI data and dMRI
datasets from cardiology.
The use of spatially adaptive
smoothing methods allows, in comparison to a voxelwise decision,
for an improved sensitivity and specitivity of signal detection
and, in contrast to nonadaptive approaches, to preserve
information about the shape of regions of interest.
Figure 3 provides a comparison for one fMRI series.
Fig. 3:
Comparison of
signal detection methods in fMRI: voxelwise decision (left),
adaptive spatial smoothing (AWS) (center), and nonadaptive spatial
smoothing (right)
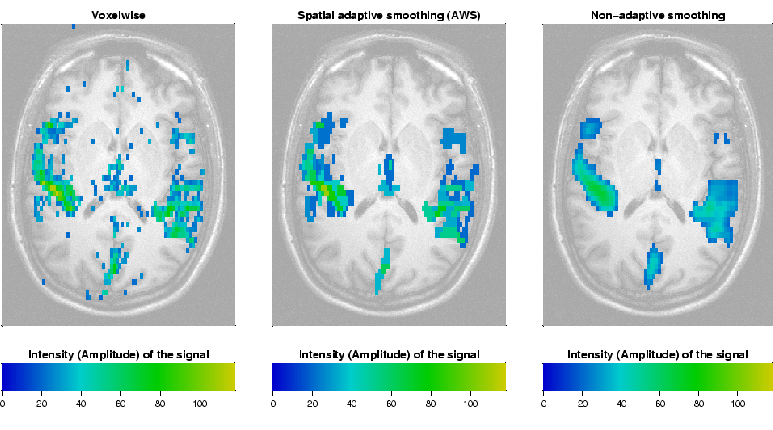 |
- Analysis of bio-signals: Synchronization effects are supposed to play the
key role in information processing in the brain. These effects
have been observed in invasive and non-invasive experimental data
([49]). In order to improve the understanding of
intrinsic neural activity, we study phase synchronization effects
in empirical multivariate brain signals by a novel segmentation
method ([19]). It allows the detection of mutually
phase-synchronized states in multivariate signals. The algorithm
combines the k-means cluster algorithm for toroidal topologies and
the statistical estimation of the synchronization strength
[18, 19]. Applications to
simulated metastable multivariate time series from stochastic and
chaotic systems reveal its properties successfully. First
applications to brain signals are successful.
- Modeling of financial time series and volatility
estimation: Time series models with varying coefficients are
appropriate for a wide range of financial time series. In
[26], a pointwise adaptive approach for
volatility modeling of financial time series is developed.
[16] extends this procedure to the case of
multidimensional financial time series. Appropriate methods for
locally stationary time series are investigated in
[9] and [10]. In
[27], the pointwise adaptive approach is applied
for the estimation and forecasting of the volatility of financial time
series. The approach is based on the assumption of local
homogeneity: for every time point there exists an interval of time
homogeneity in which the parameters of the volatility model can be
well approximated by a constant. The procedure recovers for each
point the maximal interval of homogeneity from the data using a
local change point analysis. Afterwards the estimate of the
volatility is simply obtained by local averaging. The performance
of the procedure is investigated both from a theoretical point of
view and through Monte Carlo simulations. The new procedure is
applied to some data sets and compared with the LAVE procedure
from [26] and a standard GARCH model. The
numerical results demonstrate a very reasonable performance of the
new method.
Fig. 4:
Volatility modeling
of the DAX data from 1999 to 2003 by parametric GARCH(1,1), AWS
for semiparametric GARCH(1,1), and local constant volatility AWS
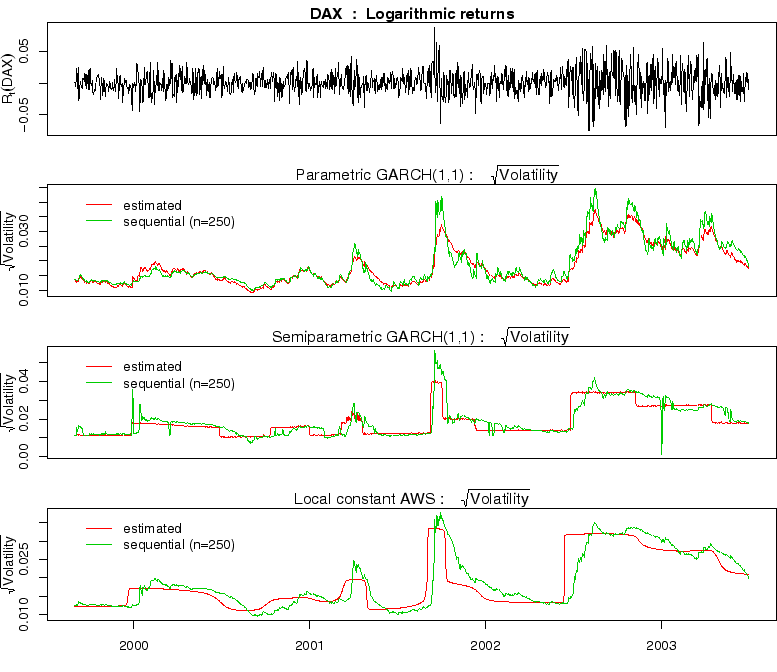 |
The adaptive weights smoothing approach has been generalized to
time varying GARCH models and semiparametric GARCH models in
[37]. The procedure involves new ideas on
localization of GARCH models. Simulations and applications on
financial data show that phenomena like long-range dependence and
heavy tails, which are often considered as inherent to financial
time series, can as well be interpreted by nonstationarity.
Both the semiparametric GARCH(1,1) and the local constant AWS
volatility model can be used to analyze the local stationarity
structure. They allow for an improved volatility prediction and
explain the observed heavy tails of the logarithmic returns.
Applications of the methodology are intended in cooperation with
the project Applied mathematical finance.
Figure 4 illustrates volatility estimates obtained
for the time series of DAX values.
Nonparametric filters often involve some filtering parameters.
These parameters can be chosen to optimize the performance locally
at each time point or globally over a time interval. In
[5], the filtering parameters are obtained
minimizing the prediction error for a large class of filters.
Under a general martingale setting, with mild conditions on the
time series structure and virtually no assumption on filters, the
adaptive filter with filtering parameter chosen on the basis of
historical data
is shown to perform nearly as well as the one with the ideal
filter in the class, in terms of filtering errors. The theoretical
result is also verified via intensive simulations. The approach
can be used to choose the order of parametric models such as AR or
GARCH processes. It can also be applied to volatility estimation
in financial economics.
- Tail index estimation:
The tail index is used to characterize the tail behavior of a
distribution. This is important, e.g., for extreme value statistics
and risk assessment. The results on tail index estimation will be
used in cooperation with the project Applied mathematical finance.
In [14], the pointwise adaptive approach is
extended to tail index estimation. The approach is based on
approximation by an exponential model. The proposed procedure
adaptively selects the number of upper order statistics used in
the estimation of the tail of the distribution function. The
selection procedure consists in consecutive testing the
hypothesis of homogeneity of the estimated parameter against the
change-point alternative. The selected number of upper order
statistics corresponds to the first detected change-point. The
main results are non-asymptotic and state optimality of the
proposed method in the ``oracle'' sense.
A similar idea is used for tail index estimation by adaptive
weights smoothing in [35].
- Classification:
In [35], a spatially adaptive discriminant
analysis procedure based on the local likelihood AWS for binary
regression is proposed. This approach is currently extended using
the specific bias-variance decomposition of classification
problems. First simulation results show potential for improvements
over [35] and classical procedures.
Figure 5 provides results of a simulation study for
three types of classifiers. Illustrated is the dependence of the
classification error on the main parameter of the procedures.
Fig. 5:
Comparison of
classification errors for a simulated example
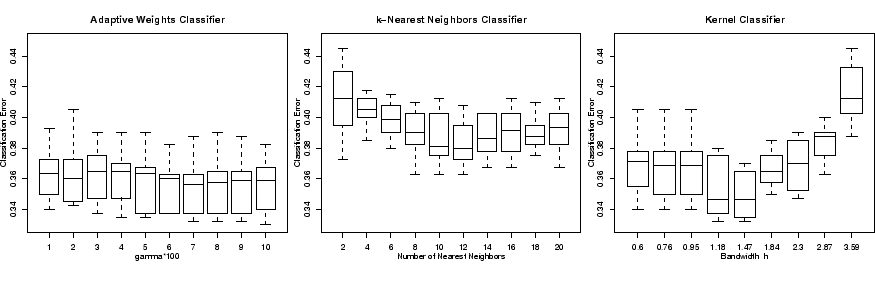 |
- Density estimation: An
adaptive weights procedure for density estimation has been
obtained using the asymptotic equivalence of density estimation
and Poisson regression ([35]). This approach is
currently extended to cover piecewise smooth densities, see
[15].
- Cluster analysis and data mining: The research has been focused on the
validation of cluster analysis results ([30]). An
automatic validation technique that becomes a general validation
tool for all hierarchical clustering methods available in the
statistical software ClusCorr98® is under development. This built-in
validation via resampling techniques is based on the
adjusted Rand index applied to contingency tables, which are
obtained by crossing two partitions. Both the appropriate number
of clusters can be validated and the stability of each cluster can
be assessed.
Bootstrap samples and subsets are equivalent to the choices of
weights of observations. This is used to make resampling
computationally effective. The built-in validation is an automatic
technique with default values for the parameters of the
simulations.
Fig. 6:
Obtained clusters and
summary of validation results for Ward's method
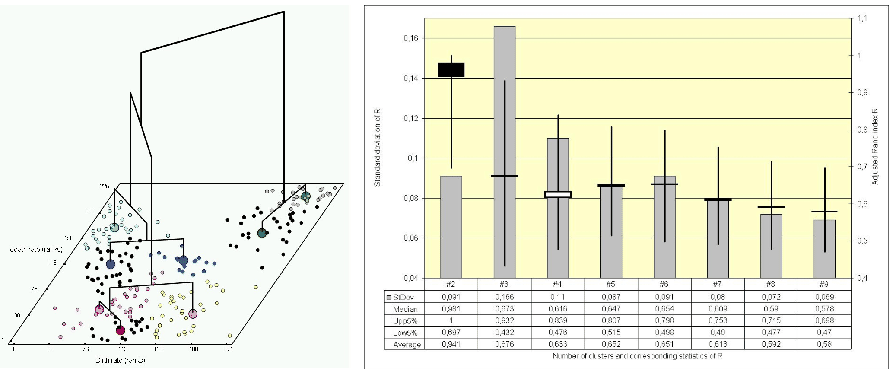 |
For illustration purposes observed birth and death rates from 225
countries are investigated. Ranks are used for hierarchical
clustering by Ward's minimum variance method. The stability
of the result is investigated by random weighting of observations.
In doing so, 200 such replicates were clustered by Ward's
method.
Figure 6 illustrates the obtained clusters
(left) and the statistics used to validate the result (right). The
unique solution is compared with results from the bootstrap
samples by the adjusted Rand index R. The axis at the left-hand
side and the bars in the graphic are assigned to the standard
deviation of R, whereas the axis at the right-hand side scales
box-plots showing median, mean, upper, and lower 5 percent quantile
of R. The median of R for K = 2 is near to its theoretical
maximum value 1. That means, the two cluster solution is stable.
It can be confirmed to a high degree for almost all samples. For
more than two clusters, the median (or mean) of the adjusted Rand
values is much smaller. Therefore the number of clusters K = 2 is
the most likely one.
(J. Pohlzehl, V. Spokoiny).
Data sets from economy or finance are often high dimensional.
Usually many characteristics of a firm or an asset are monitored
without knowledge which characteristics are needed to answer
specific questions. Data structures often do not allow for simple
parametric models. Nonparametric statistical modeling of such
data suffers from the curse of dimensionality problem (high-dimensional data are very sparse).
Fortunately, in many cases structures in complex high-dimensional
data live in low-dimensional, but usually unknown subspaces. This
property can be used to construct efficient procedures to
simultaneously identify and estimate the structure inherent to the
data set. The most common models in this context are additive
models, single- and multi-index models and partial linear models.
These models focus on index vectors or dimension reduction spaces
which allow to reduce the dimensionality of the data without
essential loss of information. They generalize classic linear
models and constitute a reasonable compromise between too
restrictive linear and too vague pure nonparametric modeling.
Indirect methods of index estimation like the nonparametric least
squares estimator, or nonparametric maximum likelihood estimator
have been shown to be asymptotically efficient, but their
practical applications are very restricted. The reason is that
their evaluation leads to an optimization problem in a
high-dimensional space, see [20]. In contrast,
computationally straightforward direct methods like the average
derivative estimator, or sliced inverse regression behave far from
optimally, again due to the ``curse of dimensionality'' problem.
[17] developed a structural adaptive
approach to dimension reduction using the structural assumptions
of a single-index and multi-index
model. The method allows for an
asymptotically efficient estimation of the dimension reduction
space and of the link function. [47] improves on
these procedures for single- and multi-index models and generalizes it to the case of partially linear models
and partially linear multi-index models.
[45] proposes a new method for partially
linear models whose nonlinear component is completely unknown. The
target of analysis is identification of regressors which enter in
a nonlinear way in the model, and complete estimation of the model
including slope coefficients of the linear component and the link
function of the nonlinear component. The procedure allows for
selecting the significant regression variables. As a by-product, a
test that the nonlinear component is M -dimensional for
M = 0, 1, 2,... is developed. The proposed approach is fully
adaptive to the unknown model structure and applies under mild
conditions on the model. The only important assumption is that the
dimensionality of the nonlinear component is relatively small.
Theoretical results indicate that the procedure provides a
prescribed level of the identification error and estimates the
linear component with an accuracy of order
n-1/2 . A
numerical study demonstrates a very good performance of the method
even for small or moderate sample sizes.
(P. Mathé,
V. Spokoiny).
Ill-posed equations arise frequently in the context of inverse
problems, where it is the aim to determine
some unknown characteristics of a physical system from data
corrupted by measurement errors.
The problem of reconstructing a planar convex set from noisy
observations of its moments is considered
in [12] . An estimation method based on
pointwise recovering of the support function of the set is
developed. We study intrinsic accuracy limitations in the
shape-from-moments estimation problem by establishing a lower
bound on the rate of convergence of the mean squared error. It is
shown that the proposed estimator is near-optimal in the sense of
the order. An application to tomographic reconstruction is
discussed, and it is indicated how the proposed estimation method
can be used for recovering edges from noisy Radon data. This
constitutes a first step to adaptive estimation procedures for
Positron Emission Tomography (PET).
For ill-posed problems it is often impossible to get sensible
results unless special methods, such as Tikhonov regularization,
are used. Work in this direction is carried out in collaboration
with S.V. Pereverzev, RICAM Linz. We study linear problems where
an operator A acts injectively and is compact in some Hilbert
space, and the equation is disturbed by noise. Under a
priori smoothness assumptions on the exact solution x, such
problems can be regularized. Within the present paradigm,
smoothness is given in terms of general source conditions,
expressed through the operator A as
x =  (A * A)v, | v|
(A * A)v, | v|  R, for some increasing function
R, for some increasing function
 ,
, 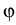 (0) = 0. This approach allows to treat regularly and
severely ill-posed problems in the same way.
The deterministic theory for such equations was developed
in [23, 24], including discretization and adaptation to
unknown source conditions.
The statistical setup is more complicated. However, based on the
seminal
work by [31], we could also extend this, including several
ill-posed problems as studied by [13, 50].
One is often not interested in the calculation of the complete
solution x, but only in some functional, say,
(0) = 0. This approach allows to treat regularly and
severely ill-posed problems in the same way.
The deterministic theory for such equations was developed
in [23, 24], including discretization and adaptation to
unknown source conditions.
The statistical setup is more complicated. However, based on the
seminal
work by [31], we could also extend this, including several
ill-posed problems as studied by [13, 50].
One is often not interested in the calculation of the complete
solution x, but only in some functional, say,
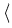 z, x
z, x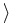 of it, where z is given afore-hand. If this is the
case, then the linear functional strategy, as proposed by Anderssen ([1]) is
important. Previous analysis of this strategy is extended, as
carried out in [25] to the present setup.
of it, where z is given afore-hand. If this is the
case, then the linear functional strategy, as proposed by Anderssen ([1]) is
important. Previous analysis of this strategy is extended, as
carried out in [25] to the present setup.
The analysis of ill-posed problems under general source conditions
raises many new issues and bridges between approximation theory
and interpolation theory in function spaces.
Natural inference problems for parameters in stochastic processes
lead to ill-posed inverse problems. A first instance is the
problem of nonparametric estimation of the weight measure a in
the stochastic delay differential equation
dX(
t) =
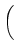
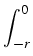 X
X(
t +
u) d
a(
u)
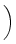
d
t +
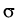
d
W(
t), 0
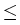 t
t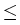 T
T,
where 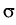 > 0 is constant and W denotes Brownian motion. In
[40], it is shown that this inference problem for
T
> 0 is constant and W denotes Brownian motion. In
[40], it is shown that this inference problem for
T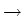
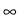 is equivalent to an integral equation with stochastic
errors in the kernel and in the right-hand side, which can be
regularized and solved by the Galerkin method. An adaptive wavelet
thresholding method is proposed in [41], which
attains the minimax rates for classes of weight measures a with
Lebesgue densities in Besov spaces. An algorithm based on the
wavelet-Galerkin method for general ill-posed linear problems is
proposed in [6]. The problem of estimating the
length of the delay in models with continuous weight densities is
treated in [42], where it is related to change-point
detection in ill-posed settings.
is equivalent to an integral equation with stochastic
errors in the kernel and in the right-hand side, which can be
regularized and solved by the Galerkin method. An adaptive wavelet
thresholding method is proposed in [41], which
attains the minimax rates for classes of weight measures a with
Lebesgue densities in Besov spaces. An algorithm based on the
wavelet-Galerkin method for general ill-posed linear problems is
proposed in [6]. The problem of estimating the
length of the delay in models with continuous weight densities is
treated in [42], where it is related to change-point
detection in ill-posed settings.
A surprising fact is that in the classical scalar diffusion model
dX(
t) =
b(
X(
t))
dt +
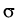
(
X(
t))
dW(
t), 0
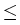 t
t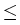 T
T,
ill-posedness arises due to the lack of continuous-time
observations. Assuming that b has regularity s - 1 and 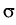 has regularity s, estimators based on the low-frequency
observations
(X(n
has regularity s, estimators based on the low-frequency
observations
(X(n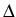 ))0
))0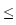 n
n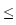 N with large N, but
arbitrary
N with large N, but
arbitrary 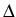 > 0 are constructed in [11]. They
attain the optimal minimax rate
N-s/(s+3) for
> 0 are constructed in [11]. They
attain the optimal minimax rate
N-s/(s+3) for 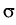 and
N-(s-1)/(2s+3) for b. The significant loss compared to the
situation of high-frequency or continuous-time observations is due
to the loss of information about the continuous path properties.
The estimators are based on spectral estimation of the underlying
Markov transition generator and are modified to a larger model
class in [43].
and
N-(s-1)/(2s+3) for b. The significant loss compared to the
situation of high-frequency or continuous-time observations is due
to the loss of information about the continuous path properties.
The estimators are based on spectral estimation of the underlying
Markov transition generator and are modified to a larger model
class in [43].
(D. Belomestny, J. Polzehl, V. Spokoiny).
In cooperation with the project Applied mathematical
finance a root-N consistent Monte Carlo estimator for a
diffusion density ([28]) has been developed. The
approach has been applied to an environmental problem
([3]) and extended to a large class of models for
stochastic processes in discrete time ([29]). These
models allow in particular for realistic estimation of ruin
probabilities in finance.
In [2], new algorithms for the evaluation of
American options using consumption processes are proposed. The
approach is based on the fact that an American option is
equivalent to a European option with a consumption process
involved. A new method of sequential improvement of an initial
approximation based on step-by-step interchanging between lower
and upper bounds is developed. Various smoothing techniques are
used to approximate the bounds in each step and hence to reduce
the complexity of algorithm. The results of numerical experiments
confirm efficiency of the algorithms proposed. Applications are
intended within the project Applied mathematical finance.
Simulation-extrapolation-type estimators in errors-in-variables
models are investigated in [38,
39]. These estimates generalize and improve
proposals from [7, 48].
References:
- R.S. ANDERSSEN, The
linear functional strategy for improperly posed problems, Inverse
Probl., 77 (1986), pp. 11-30.
- D. BELOMESTNY, G.N. MILSTEIN,
Monte Carlo evaluation of American options using consumption
processes, in preparation.
- E. VAN DEN BERG, A.W. HEEMINK, H.X. LIN, J.G.M. SCHOENMAKERS,
Probability density estimation in stochastic environmental
models using reverse representations,
Applied Mathematical Analysis Report no. 6, TU Delft, 2003, to appear in: J. Stoch. Environm. Research
& Risk Assessment.
- T. CAI, B. SILVERMAN,
Incorporating information on neighboring coefficients into
wavelet estimation, Sankhy
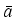 , Ser. B, 63 (2001),
pp. 127-148.
, Ser. B, 63 (2001),
pp. 127-148.
- M.-Y. CHENG, J. FAN, V. SPOKOINY, Dynamic nonparametric filtering with
application to finance, in: Recent Advances and Trends in
Nonparametric Statistics, M.G. Acritas, D.N. Politis, eds., Elsevier,
Amsterdam, Oxford, Heidelberg, 2003, pp. 315-333.
- A. COHEN, M. HOFFMANN, M. REISS,
Adaptive wavelet Galerkin methods for linear inverse
problems, to appear in: SIAM J. Numer. Anal.
- J.R. COOK, L.A. STEFANSKI,
Simulation-extrapolation estimation in parametric measurement error models,
J. Am. Stat. Assoc., 89 (1994), pp. 1314-1328.
- R. FRIEDRICH, J. PEINKE,
CH. RENNER, How to quantify deterministic and random
influences on the statistics of the foreign exchange market,
Phys. Rev. Lett., 84 (2000), 5224.
- M. GIURCANU, V. SPOKOINY,
Confidence estimation of the covariance function of stationary and
locally stationary processes,
WIAS Preprint no. 726, 2002, submitted.
- M. GIURCANU, V. SPOKOINY, R. VON SACHS,
Pointwise adaptive modeling of locally stationary time
series, in preparation.
- E. GOBET, M. HOFFMANN, M. REISS,
Nonparametric estimation of scalar diffusions based on low
frequency data, to appear in: Ann. Statist.
- A. GOLDENSHLUGER, V. SPOKOINY,
On the shape-from-moments problem and recovering edges from
noisy Radon data, WIAS Preprint no. 802, 2002, Probab. Theory
Related Fields, 128 (2004), pp. 123-140.
- G.K. GOLUBEV,
R.Z. KHASMINSKI, A statistical approach to some inverse
problems for partial differential equations, Probl. Peredachi
Inf., 35 (1999), pp. 51-66.
- I. GRAMA, V. SPOKOINY,
Tail index estimation by local exponential modeling, WIAS
Preprint no. 819, 2003.
- I. GRAMA, J. POLZEHL, V. SPOKOINY,
Adaptive estimation for varying coefficient generalized linear
models, in preparation.
- W. HÄRDLE, H. HERWATZ, V. SPOKOINY,
Time inhomogeneous multiple volatility modeling,
J. Financial Econometrics, 1 (2003), pp. 55-95.
- M. HRISTACHE, A. JUDITSKY,
J. POLZEHL, V. SPOKOINY,
Structure adaptive approach for dimension reduction,
Ann. Statist., 29 (2001), pp. 1537-1566.
- A. HUTT, H. RIEDEL,
Analysis and modeling of quasi-stationary multivariate time
series and their application to middle latency auditory evoked
potentials, Physica D, 177 (2003), pp. 203-232.
- A. HUTT, A. DAFFERTSHOFER,
U. STEINMETZ, Detection of mutual phase synchronization in
multivariate signals and application to phase ensembles and
chaotic data, Phys. Rev. E, 68 (2003), 036219.
- R.L. KLEIN, R.H. SPADY,
An efficient semiparametric estimator for binary response models,
Econometrica, 61 (1993), pp. 387-421.
- P. MATHÉ, The general
functional strategy under general source conditions, submitted.
- P. MATHÉ, S.V. PEREVERZEV,
Optimal error of ill-posed problems in variable
Hilbert scales under the presence of white noise, manuscript.
- ,
Discretization strategy for ill-posed problems in variable
Hilbert scales, Inverse Probl., 19 (2003), pp. 1263-1277.
- ,
Geometry of ill-posed problems in variable
Hilbert scales, Inverse Probl., 19 (2003), pp. 789-803.
- ,
Direct estimation of linear functionals from indirect noisy
observations, J. Complexity, 18 (2002),
pp. 500-516.
- D. MERCURIO, V. SPOKOINY,
Statistical inference for time-inhomogeneous volatility
models, to appear in: Ann. Statist.
- ,
Estimation of time dependent volatility via local change point
analysis, WIAS Preprint no. 904, 2004.
- G.N. MILSTEIN, J.G.M. SCHOENMAKERS,
V. SPOKOINY,
Transition density estimation for stochastic differential
equations via forward-reverse representations,
WIAS Preprint no. 680, 2001, Bernoulli, in print.
- G.N. MILSTEIN, J.G.M. SCHOENMAKERS,
V. SPOKOINY,
Forward-reverse representations for Markov chains, in
preparation.
- H.-J. MUCHA, H.-G. BARTEL,
ClusCorr98 -- Adaptive clustering, multivariate
visualization, and validation of results, to appear in: Proceedings of the 27th
Annual Conference of the GfKl, Springer, Berlin.
- M.S. PINSKER, Optimal
filtration of square-integrable signals in Gaussian noise,
Probl. Inf. Transm., 16 (1980), pp. 52-68.
- J. POLZEHL, V. SPOKOINY,
Image denoising: Pointwise adaptive approach,
Ann. Statist., 31 (2003), pp. 30-57.
- ,
Adaptive weights smoothing with applications to image
restoration, J.R. Stat. Soc., Ser. B, 62
(2000), pp. 335-354.
- ,
Functional and dynamic Magnetic Resonance Imaging using
vector adaptive weights smoothing,
J.R. Stat. Soc., Ser. C, 50 (2001), pp. 485-501.
- ,
Local likelihood modeling by adaptive weights smoothing,
WIAS Preprint no. 787, 2002.
- ,
Varying coefficient regression modeling
by adaptive weights smoothing, WIAS Preprint no. 818, 2003.
- ,
Adaptive estimation for a varying coefficient (E)GARCH
model, in preparation.
- J. POLZEHL, S. ZWANZIG,
On a symmetrized extrapolation estimator in linear
errors-in-variables models, Comput. Stat. Data Anal., in print.
- ,
On a comparison of different simulation extrapolation estimators in linear errors-in-variables models,
U.U.D.M. Report no. 17, Uppsala University, 2003.
- M. REISS, Minimax rates for
nonparametric drift estimation in affine stochastic delay
differential equations,
Stat. Inference Stoch. Process., 5 (2002), pp. 131-152.
- ,
Adaptive
estimation for affine stochastic delay differential equations,
submitted.
- , Estimation of the
delay length in affine stochastic delay differential equations,
submitted.
- ,
Nonparametric volatility estimation on the
real line from low-frequency observations, submitted.
- H. RISKEN, The
Fokker-Planck Equation, Springer, Berlin, Heidelberg, 1996.
- A. SAMAROV, V. SPOKOINY,
C. VIAL, Component identification and estimation in nonlinear
high-dimensional regression models by structural adaptation,
WIAS Preprint no. 828, 2003.
- V. SPOKOINY,
Estimation of a function with discontinuities via local polynomial
fit with an adaptive window choice,
Ann. Statist., 26 (1998), pp. 1356-1378.
- V. SPOKOINY, Y. XIA,
Effective dimension reduction by structural adaptation,
in preparation.
- L.A. STEFANSKI, J.R. COOK,
Simulation-extrapolation: The measurement error jackknife,
J. Am. Stat. Assoc., 90 (1995),
pp. 1247-1256.
- A. STURM, P. KÖNIG,
Mechanisms to synchronize neuronal activity, Biol. Cyb.,
84 (2001), pp. 153-172.
- A. TSYBAKOV, On the best
rate of adaptive estimation in some inverse problems, C.R.
Acad. Sci. Paris Sér. I Math., 330 (2000), pp. 835-840.
LaTeX typesetting by I. Bremer
2004-08-13





