Collaborator: W. Dreyer
,
M. Herrmann
Cooperation with: M. Kunik (Otto-von-Guericke-Universität Magdeburg),
M. Junk (Universität Kaiserslautern)
Supported by: DFG: Priority Program ``Analysis und Numerik von
Erhaltungsgleichungen'' (ANumE - Analysis and numerics for
conservation laws)
Description:
At low temperatures the evolution of heat in crystalline solids is carried
by phonons. In particular, the classical Fourier theory of heat
fails to describe heat conduction at low temperatures, where the evolution
of a phonon gas is governed by the Boltzmann-Peierls equation which
is a kinetic equation for the phase density of phonons. For more details we
refer to [4] and [5]. In [4] we have shown that
the full Boltzmann-Peierls equation can be reduced to the
simplified kinetic equation
| 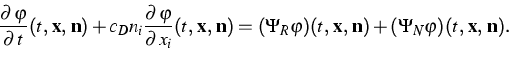 |
(1) |
In (1), 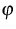 is a reduced phase density depending on
time t, space
is a reduced phase density depending on
time t, space 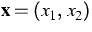 , and a normal vector
, and a normal vector
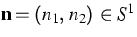 ; and the positive constant
cD is the Debye speed. For simplicity we consider
(1) in two space dimensions only. In addition to the
reduced equation (1) we introduce a reduced definition of
the (entropy density h / entropy flux
; and the positive constant
cD is the Debye speed. For simplicity we consider
(1) in two space dimensions only. In addition to the
reduced equation (1) we introduce a reduced definition of
the (entropy density h / entropy flux 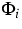 ) pair according
to
) pair according
to
| 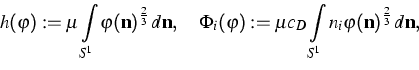 |
(2) |
where 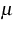 is a given constant. We have proved that these definitions and
the kinetic equation (1) imply the entropy inequality
is a given constant. We have proved that these definitions and
the kinetic equation (1) imply the entropy inequality
| 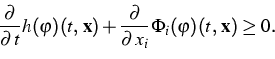 |
(3) |
As well as the phase density, also the reduced phase density 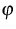 can
be used to define moments. The following moments have an immediate physical
interpretation
can
be used to define moments. The following moments have an immediate physical
interpretation
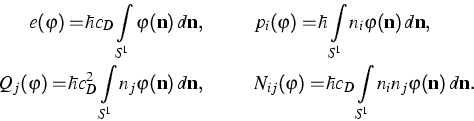
The fields e, pi, Qi, and Nij denote the energy
density, the momentum density, the heat flux, and the momentum flux,
respectively. From a physical point of view, the moments of 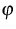 are more important than
are more important than 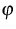 itself. On the right-hand side of
(1) there are two collision operators
itself. On the right-hand side of
(1) there are two collision operators 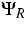 and
and 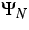 which are simplified models of two different kinds of
interaction processes, which are called R-processes and
N-processes. The N-processes describe phonon-phonon interactions
and conserve the energy as well as the momentum, while the
R-processes indicate interactions of phonons with lattice
impurities. The latter ones only conserve the energy. The Callaway ansatz for the collision operators reads
which are simplified models of two different kinds of
interaction processes, which are called R-processes and
N-processes. The N-processes describe phonon-phonon interactions
and conserve the energy as well as the momentum, while the
R-processes indicate interactions of phonons with lattice
impurities. The latter ones only conserve the energy. The Callaway ansatz for the collision operators reads
| 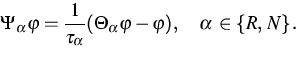 |
(4) |
Here 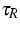 and
and 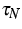 are two relaxation times, and
are two relaxation times, and 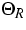 and
and 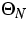 describe the phase density in the limiting
cases
describe the phase density in the limiting
cases 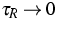 and
and 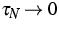 ,respectively. In particular,
,respectively. In particular, 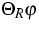 and
and 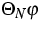 maximize the entropy according to
maximize the entropy according to
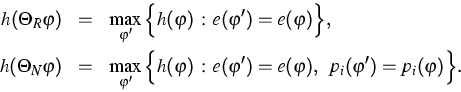
The reduced Boltzmann-Peierls equation
(1) induces an infinite number of balance equations. For
any vector 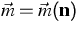 of moment weights, there is a
corresponding vector of densities
of moment weights, there is a
corresponding vector of densities 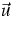 , fluxes
, fluxes 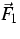 ,
,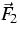 , and productions P, according to
, and productions P, according to
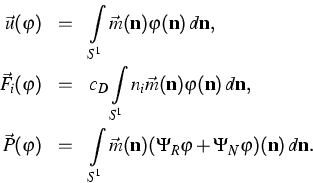
With these definitions, the kinetic equation implies
| 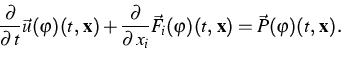 |
(5) |
Physicists and engineers are not interested in the phase density
itself, but in balance equations for moments as (12). It is a
common strategy in Extended Thermodynamics (cf. [4,
1, 3, 5]) to consider in (12) the
densities 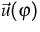 as variables. However, since the fluxes
and the productions are in general not functions of
as variables. However, since the fluxes
and the productions are in general not functions of 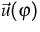 there arises the so-called closure problem. An often used and
powerful closure principle is the Maximum Entropy Principle. It
has the advantages that
there arises the so-called closure problem. An often used and
powerful closure principle is the Maximum Entropy Principle. It
has the advantages that
- 1.
- the resulting moment systems are hyperbolic, after a suitable
transformation, they are even symmetric hyperbolic;
- 2.
- there exists a corresponding entropy inequality.
The Maximum Entropy Principle (MEP) can be formulated as follows.
We start with a fixed vector of densities 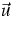 with N components. In
the first step, we determine the corresponding MEP projector
with N components. In
the first step, we determine the corresponding MEP projector 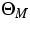 so that, for any given
so that, for any given 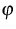 , there holds
, there holds
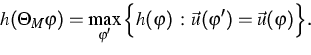
In the second step we use 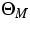 in order to solve the closure
problem of the system (12). When we replace
formally the phase density
in order to solve the closure
problem of the system (12). When we replace
formally the phase density 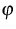 by
by 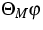 , we obtain
the resulting MEP system
, we obtain
the resulting MEP system
| 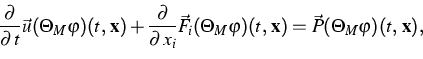 |
(6) |
which is indeed a closed system for the variables 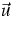 .
.
In the year 2001 we have studied the following problems:
- 1.
- Derivation of the reduced equation and the corresponding
reduced entropy inequality
We have proved that the reduced
equation contains all important information on the solutions of the
original Boltzmann-Peierls equation. Furthermore, we have
derived the reduced entropy (2) from the original
Bose entropy so that
- (a)
- there holds the entropy inequality (3),
- (b)
- the MEP applied to the original Boltzmann-Peierls equation and to the reduced equation (1) lead
to identical moment systems.
- 2.
- Existence of MEP-operators
The existence of MEP operators is a crucial problem. Junk has shown
in [3] that in the most prominent application of the Maximum
Entropy Principle, which is the Boltzmann equation for monatomic
gases, MEP operators fail to exist within a reasonable domain of
definition. In [1] we have proved that in the case of the Boltzmann-Peierls equation, the Maximum Entropy Principle will lead to
well-defined MEP operators  , if it is applied to the reduced
entropy.
, if it is applied to the reduced
entropy.
- 3.
- Kinetic approximations and kinetic schemes
Corresponding to the MEP system (13) there exists the
following modified kinetic equation
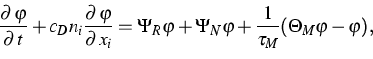
where 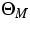 is the MEP operator corresponding to
is the MEP operator corresponding to 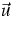 (cf. [1]) and
(cf. [1]) and 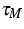 is an artificial relaxation
time. The moment system (13) formally results in the limit
is an artificial relaxation
time. The moment system (13) formally results in the limit
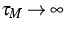 . This approach illustrates the close
connection between the kinetic equation and the MEP system.
. This approach illustrates the close
connection between the kinetic equation and the MEP system.
Furthermore there exists a class of consistent kinetic schemes
containing schemes for the kinetic equation as well as for the moment
systems. For the details we refer to [1].
- 4.
- Numerical simulations
A numerical example shall illustrate that the MEP systems induce a sequence
of approximations of the kinetic equation. To this end we study the
evolution of an initial energy pulse as shown in Fig. 1.
Fig. 1:
Initial energy pulse
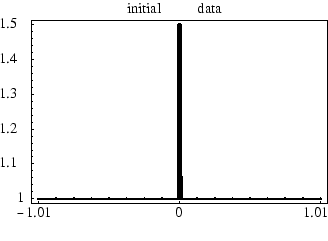
|
For simplicity we set 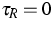 , and we assume that all quantities do not
depend on the x2 direction. Furthermore we set
, and we assume that all quantities do not
depend on the x2 direction. Furthermore we set 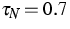 , cD=0.5. The initial data
, cD=0.5. The initial data 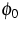 are determined by an
equilibrium assumption, i.e.
are determined by an
equilibrium assumption, i.e. 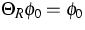 . The
evolution of the energy pulse according to the kinetic equation is
depicted in Fig. 2. The figures show the corresponding
solutions of various MEP systems.
. The
evolution of the energy pulse according to the kinetic equation is
depicted in Fig. 2. The figures show the corresponding
solutions of various MEP systems.
![\begin{figure}
\makeatletter
\@DreiProjektbilderNocap[h]{0.28\textwidth}{001.eps}{002.eps}{003.eps}
\makeatother\end{figure}](../2001/img488.gif)
![\begin{figure}
\makeatletter
\@DreiProjektbilderNocap[h]{0.28\textwidth}{011.eps}{012.eps}{013.eps}
\makeatother\end{figure}](../2001/img489.gif)
![\begin{figure}
\makeatletter
\@DreiProjektbilderNocap[h]{0.28\textwidth}{041.eps}{042.eps}{043.eps}
\makeatother\end{figure}](../2001/img490.gif)
![\begin{figure}
\makeatletter
\@DreiProjektbilderNocap[h]{0.28\textwidth}{021.eps}{022.eps}{023.eps}
\makeatother\end{figure}](../2001/img491.gif)
Fig. 2:
Solution of a MEP system with 81 moments
![\makeatletter
\@DreiProjektbilderNocap[h]{0.28\textwidth}{031.eps}{032.eps}{033.eps}
\makeatother](../2001/img492.gif)
|
References:
- W. DREYER, M. HERRMANN, M. KUNIK, Kinetic
schemes and initial boundary value problems for the Euler System,
WIAS Preprint no. 607, 2000, Transport
Theory Statist. Phys., in print.
-
 , Kinetic
solutions of the Boltzmann-Peierls equation and its moment systems,
, Kinetic
solutions of the Boltzmann-Peierls equation and its moment systems,
WIAS Preprint no. 709, 2001.
- W. DREYER, M. JUNK, M. KUNIK, On the
approximation of kinetic equations by moment systems,
Nonlinearity, 14 (2001), pp. 881-906.
- W. DREYER, M. KUNIK, Kinetische Behandlung von
ausgewählten hyperbolischen Anfangs- und Randwertproblemen,
DFG Project DR 401/2-2.
- W. DREYER, H. STRUCHTRUP, Heat pulse
experiments revisited, Cont. Mech. Thermodyn., 5 (1993), pp. 3-50.
LaTeX typesetting by I. Bremer
9/9/2002
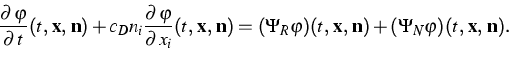
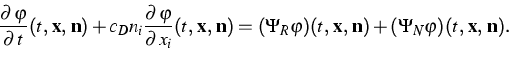
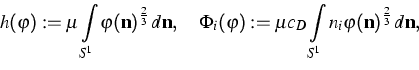
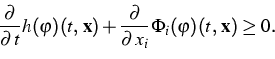
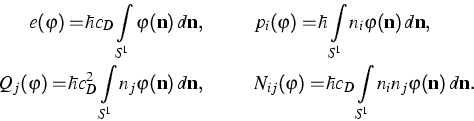
![]() are more important than
are more important than ![]() itself. On the right-hand side of
(1) there are two collision operators
itself. On the right-hand side of
(1) there are two collision operators ![]() and
and ![]() which are simplified models of two different kinds of
interaction processes, which are called R-processes and
N-processes. The N-processes describe phonon-phonon interactions
and conserve the energy as well as the momentum, while the
R-processes indicate interactions of phonons with lattice
impurities. The latter ones only conserve the energy. The Callaway ansatz for the collision operators reads
which are simplified models of two different kinds of
interaction processes, which are called R-processes and
N-processes. The N-processes describe phonon-phonon interactions
and conserve the energy as well as the momentum, while the
R-processes indicate interactions of phonons with lattice
impurities. The latter ones only conserve the energy. The Callaway ansatz for the collision operators reads
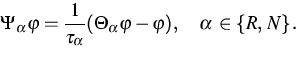
![]() of moment weights, there is a
corresponding vector of densities
of moment weights, there is a
corresponding vector of densities ![]() , fluxes
, fluxes ![]() ,
,![]() , and productions P, according to
, and productions P, according to
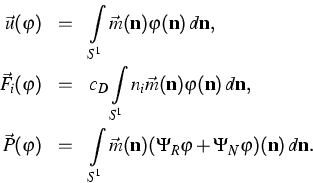
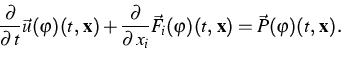
![]() with N components. In
the first step, we determine the corresponding MEP projector
with N components. In
the first step, we determine the corresponding MEP projector ![]() so that, for any given
so that, for any given ![]() , there holds
, there holds
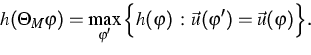
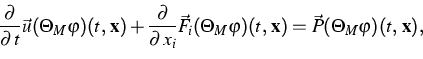
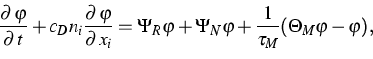
![\begin{figure}
\makeatletter
\@DreiProjektbilderNocap[h]{0.28\textwidth}{001.eps}{002.eps}{003.eps}
\makeatother\end{figure}](../2001/img488.gif)
![\begin{figure}
\makeatletter
\@DreiProjektbilderNocap[h]{0.28\textwidth}{011.eps}{012.eps}{013.eps}
\makeatother\end{figure}](../2001/img489.gif)
![\begin{figure}
\makeatletter
\@DreiProjektbilderNocap[h]{0.28\textwidth}{041.eps}{042.eps}{043.eps}
\makeatother\end{figure}](../2001/img490.gif)
![\begin{figure}
\makeatletter
\@DreiProjektbilderNocap[h]{0.28\textwidth}{021.eps}{022.eps}{023.eps}
\makeatother\end{figure}](../2001/img491.gif)