Stress analysis of a thin wafer

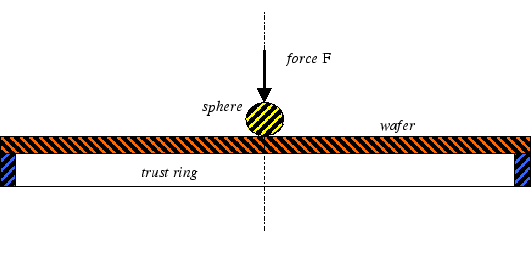
In 2000 we have started a remittance study on the stress distribution in a thin wafer plate which is loaded by the steel sphere according to Fig. 1.

**Fig. 1:** Experimental device
$%% \ProjektEPSbildNocap {0.8\textwidth}{pl1.eps}$

The wafer plate's material is single crystal GaAs the [100] direction of which is parallel to the load axes. Preliminary studies have shown that the external load induces a deformation field that has small strain components, however, the rotational contribution to the deformation field is quite large, so that the appropriate field equations are the nonlinear von Kármán equations in Lagrangian coordinates. The complete elliptic von Kármán system is to be found in the WIAS Annual Report 2000, and we refer the reader to pp. 120-122. The von Kármán system results, by a limiting process, from the 3-d nonlinear elasticity system for the second Piola-Kirchhoff stress tensor

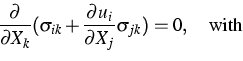$\begin{displaymath} \frac{\partial }{\partial X_{k}}(\sigma _{ik}+\frac{\partial u_{i}}{\partial X_{j}}\sigma _{jk})=0,\quad \text{with}\end{displaymath}$

(1)

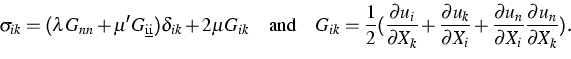$\begin{displaymath} \sigma _{ik}=(\lambda G_{nn}+\mu ^{\prime }G_{\text{\b{i}\b{... ...l u_{n}}{\partial X_{i}}\frac{\partial u_{n}}{\partial X_{k}}).\end{displaymath}$

(2)

During the time of the current annual report we finished all necessary calculations, and we proceeded according to the following items:

1. The von Kármán system revisited
We have rederived the von Kármán system from a different point of view as it was considered in the year 2000. While we started at first from special kinematic assumptions in order to reduce the cubic anisotropic 3-d system of elasticity to the von Kármán system, the new derivation relies on some simple assumptions regarding the dependence of the displacement and stress components u_i and $\sigma _{ij}$ ,respectively, on the thickness h of the plate. In particular, we now conclude, relying on an asymptotic expansion for the displacement, that the main contributions to the displacements are of the form

u₁ = $\displaystyle-\partial _{X}W\left( X,Y\right) Z+U\left( X,Y\right) +O(h^{3}),$

u₂ = $\displaystyle-\partial _{Y}W\left( X,Y\right) Z+V\left( X,Y\right) +O(h^{3}),$ (3)

u₃ = $\displaystyleW\left( X,Y\right) +O(h^{2}),$

2. The contact problem sphere/plate
The distribution of the load over the contact surface is given by

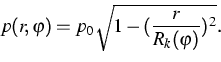$\begin{displaymath} p(r,\varphi )=p_{0}\sqrt{1-(\frac{r}{R_{k}(\varphi )})^{2}}.\end{displaymath}$

(5)

The anisotropic cubic symmetry is indicated by the function $R_{k}(\varphi )$ , which gives the boundary of the contact area that induces the isotropic steel sphere on the upper surface of the anisotropic wafer plate.

3. The boundary conditions
It is crucial for the correct modeling of the actual technical problem that in particular the boundary conditions at the thrust ring are prescribed appropriately. A comparison of the maximal displacement according to the mathematical simulation with the experimental data has revealed that the material points of the plate that coincide initially with the inner circle of the thrust ring do not remain there, rather the plate may glide without friction. This fact leads to the phenomenon that the stress resultant tensor $n_{\alpha \beta }$ is continuous across the inner thrust line. Because the plate can additionally rotate freely here, the bending moment tensor $m_{\alpha \beta }$ is also continuous across the thrust line. From preliminary test calculations we know that there are only compressive forces along the thrust line, so that the 3-component of the displacement W vanishes here.

The outer boundary of the plate is free of stress:

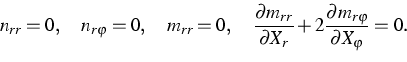$\begin{displaymath} n_{rr}=0,\quad n_{r\varphi }=0,\quad m_{rr}=0,\quad \frac{\p... ...X_{r}}+2\frac{\partial m_{r\varphi }}{\partial X_{\varphi }}=0.\end{displaymath}$

(6)

4. The numerical simulation
The von Kármán system is numerically solved by a finite element method. The finite-element net consists of triangles that have 36 degrees of freedom. The 3- displacement W is given in each of the outer nodes of an element by a 6- parameter Hermitian ansatz which is C¹ continuous. Thus the value of the ansatz function and its two first derivatives can be described. The two other displacements U and V are given in each of the outer nodes of an element by a 3- parameter Hermitian ansatz which is C⁰ continuous. Thus the value of the ansatz functions and their first derivatives can be described. Consequently, we obtain for each triangle an algebraic nonlinear coupled system for 36 unknowns with a symmetric Jacobian.

5. The Kirchhoff system
The accuracy of the used elements is tested by the Kirchhoff system, which results as the limiting case of the von Kármán system for very small bending. The elements used approximate the analytic solution of the Kirchhoff system already up to five mantissae even for a very rough net.

6. The crucial test of accuracy
The FCM has compared the maximal displacement versus the external load according to the WIAS calculation of the von Kármán system with their own careful measurements. Figure 2 shows the perfect matching of the simulation with the experimental data. It is important to note that the WIAS result is in fact a prediction, and does not contain any fitting procedure. However, if the load is increased beyond $450\;N$ , a difference between simulation and the experiment begins to grow. The range of applicability of the von Kármán system is reached, and further nonlinear contributions of the complete 3-d elasticity system must be incorporated.

**Fig. 2:** Experiment versus prediction
$%% \ProjektEPSbildNocap {0.5\textwidth}{pl2.eps}$

**Fig. 3:** Anisotropic behavior of stress components
$\makeatletter \@ZweiProjektbilderNocap[h]{0.4\textwidth}{pl3.eps}{pl4.eps} \makeatother$

u₁	=	$\displaystyle-\partial _{X}W\left( X,Y\right) Z+U\left( X,Y\right) +O(h^{3}),$
u₂	=	$\displaystyle-\partial _{Y}W\left( X,Y\right) Z+V\left( X,Y\right) +O(h^{3}),$	(3)
u₃	=	$\displaystyleW\left( X,Y\right) +O(h^{2}),$

Stress analysis of a thin wafer plate of single crystal gallium arsenide