Phase transitions

Cooperation with: S. Brodie, C.M. Brown (Heriot-Watt University Edinburgh, UK), P. Colli, G. Gilardi (Università di Pavia, Italy), S. Eichler (Freiberger Compound Materials GmbH (FCM)), T. Hauck (Motorola, München), W.H. Müller (Technische Universität Berlin), E. Radkevich (Lomonosov University, Moscow, Russia)

Supported by: BMBF: ``Mathematische Modellierung und Simulation der Entstehung, des Wachstums und der Auflösung von Arsenausscheidungen in einkristallinem Galliumarsenid'' (Mathematical modeling and simulation of the formation, growth and dissolution of arsenic precipitation in single crystal gallium arsenide - 03DRM3B5)

Description:Currently, the investigations on phase transitions were oriented towards the following tasks:

(1) In collaboration with W.H. Müller, S. Brodie, and C.M. Brown, AMF techniques have been used in order to study in-situ the motion of interfaces in various microstructures that were obtained from a melt by different cooling paths. In turn the morphological changes were compared with simulations. To this end, the grey colors of micrographs of tin/lead alloys are mapped onto concentrations so that the resulting mathematical microstructure serves as initial data for the phase-field model.

(2) For the evaluation of the mechanical part of the model, a Neumann series must be computed. This makes a convergence study necessary. It was shown that the convergence of the Neumann series depends sensitively on the different elastic tensors of tin and lead. To describe this quantitatively, various norms were compared in order to select the appropriate norm so that convergence of the Neumann series could be proved ([1]).

(3) For given initial and boundary data, the standard phase-field model that was used by Dreyer/Müller for numerical simulations of various phase separation processes in tin/lead alloys contains too many complexities. In particular, the quadratic dependence of the diffusion potential on the strain tensor renders the analysis difficult. Indeed, L^p estimates for $\nabla u$ are known to hold just for p close to 2 while global L⁴ estimates were to be required. Therefore, in order that the problem turns out to be accessible from a mathematical point of view, some simplifications have been made concerning the matrices of mobilities, the stiffness matrix, and the matrix of surface tensions in their dependencies on the concentration and on the unisotropy. For the simplified model, existence and uniqueness results were established, [2].

(4) The aforementioned difficulties of a mathematical treatment of the standard phase-field models are among the motivations of Prof. Gajewski from WIAS, who proposed an alternative mathematical model for phase separation processes. The model is a nonlocal alternative to the classical Cahn/Hilliard model, where the fourth-order derivatives do not occur any more, but are modeled now by integrals with local kernels. For the simple Cahn/Hilliard model, Gajewski and Zacharias demonstrated that the nonlocal alternative allows for the powerful maximum principle, which fails to exist for the Cahn/Hilliard equation. The extension of Gajewski's ideas to phase separation processes under thermomechanical stress fields has now been established. There results the nonlocal version of the standard Dreyer/Müller model that describes phase separation processes by a coupling of a diffusion equation of Cahn/Hilliard type and the elliptic quasi-static mechanical system for the mechanical displacement. The central quantity of the nonlocal model is the free energy functional, which is proposed according to

$\displaystyle\Psi$ = $\displaystyleU_{ther}\left( T\right) +k_{B}\int\nolimits_{\Omega }\left( c\left... ...( t,X\right) \right) \ln \left( 1-c\left( t,X\right) \right) \right) d^{3}X\ast$

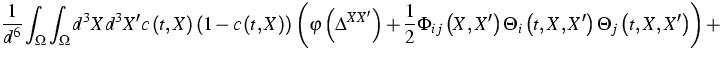
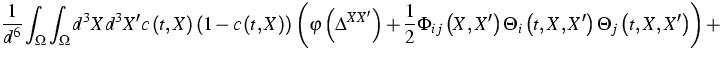
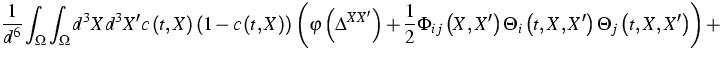
   $\displaystyle\frac{1}{d^{6}}\int\nolimits_{\Omega }\int\nolimits_{\Omega }d^{3}... ...left( t,X,X^{\prime }\right) \Theta _{j}\left( t,X,X^{\prime }\right) \right) +$

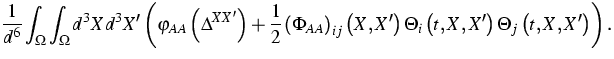
   $\displaystyle\frac{1}{d^{6}}\int\nolimits_{\Omega }\int\nolimits_{\Omega }d^{3}... ...left( t,X,X^{\prime }\right) \Theta _{j}\left( t,X,X^{\prime }\right) \right) +$

   $\displaystyle\frac{1}{d^{6}}\int\nolimits_{\Omega }\int\nolimits_{\Omega }d^{3}... ...left( t,X,X^{\prime }\right) \Theta _{j}\left( t,X,X^{\prime }\right) \right) +$

   $\displaystyle\frac{1}{d^{6}}\int\nolimits_{\Omega }\int\nolimits_{\Omega }d^{3}... ...left( t,X,X^{\prime }\right) \Theta _{j}\left( t,X,X^{\prime }\right) \right) .$ (1)

This model and a further nonlocal model for the description of intermetallic phases, which need additionally nonconserved order parameters, form the basis of the WIAS proposal Model of phase transitions with thermo-mechanical interactions to the DFG Priority Program 1095 Analysis, Modellbildung und Simulation von Mehrskalenproblemen (Analysis, modeling and simulation of multiscale problems). Here the three WIAS groups Dreyer/Gajewski/Sprekels, in collaboration with Prof. W.H. Müller, Technische Universität Berlin, and T. Hauck, Motorola München, will investigate and compare mathematically, as well as numerically and experimentally, the properties of the standard phase-field model with higher derivatives with the nonlocal model represented by integro-differential systems, containing at most second-order derivatives. Furthermore a serious data basis for the two reference materials tin/lead (conserved order parameter) and silver/tin (nonconserved order parameters) will be established.

(5) The very first period of nucleation and the subsequent evolution of liquid arsenic droplets within single crystal gallium arsenide (GaAs) were modeled and studied in collaboration with the Freiberger Compound Materials GmbH (FCM). This study is sponsored by the BMBF. The outstanding and difficult problem arises from the following process:

In order that single crystal GaAs can be appointed as a semiconductor material there is an excess content $\Delta ,0<\Delta <0.0001$ of As above the ideal single crystal As concentration c=0.5. The excess atoms occupy homogeneously in space interstitial sites, vacancy sites, and sites of the Ga sublattice. During necessary heat treatments under very high pressure, so that arsenic cannot evaporate, the excess As atoms start to diffuse and the process of liquid As-droplet formation sets in. Obviously, the initial and necessary homogeneity is lost. The objective of this project is (i) a simulation of the complete process, and (ii) the identification of the parameter which possibly can be adjusted, so that liquid droplets will not form.

The first year of this three-year project was devoted exclusively to the establishment of the mathematical model. After many discussions with the physicists in charge from FCM, it has turned out that the following items are important:

(i) There is an observed tendency that droplets appear in the vicinity of dislocations. The diffusion process is thus modeled by the Dreyer/Müller standard phase-field model that describes diffusion under inhomogeneous stress fields, which are induced here, and introduced into the model, by a given random distribution of point dislocations.

(ii) The nucleation process itself is thermodynamically far from the instability region of the parent phase. Thus the critical energy barrier and the critical droplet size can be calculated according to the classical nucleation theory. This means that a reduction of the energy barrier, which might appear according to the more advanced Cahn/Hilliard nucleation theory, has not to be considered.

(iii) The evolution of the droplet formation from a locally given content of As atoms, according to (i), was first modeled and described in the last annual report, by a dynamic generalization of the stationary and well-accepted Becker/Döring theory. However, a preliminary numerical study of the explicit system of rate equations has revealed serious deficits. For example, this system predicts droplet formation for undercritical pressure! Thus a very detailed study of the pure nucleation problem became necessary. To this end we considered the nucleation of liquid droplets in vapor as a simple reference system.

$\displaystyle\Psi$	=	$\displaystyleU_{ther}\left( T\right) +k_{B}\int\nolimits_{\Omega }\left( c\left... ...( t,X\right) \right) \ln \left( 1-c\left( t,X\right) \right) \right) d^{3}X\ast$
		$\displaystyle\frac{1}{d^{6}}\int\nolimits_{\Omega }\int\nolimits_{\Omega }d^{3}... ...left( t,X,X^{\prime }\right) \Theta _{j}\left( t,X,X^{\prime }\right) \right) +$
		$\displaystyle\frac{1}{d^{6}}\int\nolimits_{\Omega }\int\nolimits_{\Omega }d^{3}... ...left( t,X,X^{\prime }\right) \Theta _{j}\left( t,X,X^{\prime }\right) \right) +$
		$\displaystyle\frac{1}{d^{6}}\int\nolimits_{\Omega }\int\nolimits_{\Omega }d^{3}... ...left( t,X,X^{\prime }\right) \Theta _{j}\left( t,X,X^{\prime }\right) \right) +$
		$\displaystyle\frac{1}{d^{6}}\int\nolimits_{\Omega }\int\nolimits_{\Omega }d^{3}... ...left( t,X,X^{\prime }\right) \Theta _{j}\left( t,X,X^{\prime }\right) \right) .$	(1)