Thermodynamical modeling of porous and granular

[Next]:

Stability and relaxation of flows in

[Up]:

Project descriptions

[Previous]:

Wave propagation in porous and granular

[Contents]

[Index]

Thermodynamical modeling of porous and granular materials - flaws of Biot's model

Collaborator: K. Wilmanski

Cooperation with: I. Edelman (Alexander von Humboldt fellow in WIAS, Russian Academy of Sciences, Moscow), T. Wilhelm (Universität Innsbruck, Austria), C. Lai (Studio Geotecnico Italiano, Milano), R. Lancellotta (Politecnico di Torino, Italy)

Description:

Aims and results of the project

Most of the linear multicomponent models used in contemporary applications in soil mechanics and geophysics are derived from Biot's model developed at the beginning of the fourties. This model describes mechanical processes in saturated poroelastic materials by means of a two-component linear continuum. It has two essential features:

1.

In addition to classical partial accelerations in two-momentum balance equations it contains coupling terms. Momentum balance equations for the solid and fluid components have then the following form

$\displaystyle\rho ^{S}\frac{\partial {\bf v}^{S}}{\partial t}+\rho _{12}\frac{\partial {\bf v}^{F}}{\partial t}$	=	$\displaystyle{}div{\bf T}^{S}-{\bf \hat{p}},$	(1)
$\displaystyle\rho ^{F}\frac{\partial {\bf v}^{F}}{\partial t}+\rho _{12}\frac{\partial {\bf v}^{S}}{\partial t}$	=	$\displaystyle{}div{\bf T}^{F}+{\bf \hat{p},}$

where ${\bf T}^{S},{\bf T}^{F}$ are partial stress tensors, ${\bf v}^{S},{\bf v}^{F}$ denote velocities, $\rho ^{S},\rho ^{F}$ are partial mass densities, ${\bf \hat{p}}$ is the diffusive force of interaction, and $\rho _{12}$ is a mass density describing the dynamical coupling of components. It is usually related to a so-called added mass effect, and some experimentalists claim that it is related to the tortuosity of porous and granular materials.

2.

There exists a static interaction between the components which leads to the following constitutive relations for partial stresses

$\displaystyle{\bf T}^{S}$	=	$\displaystyle\lambda \left( \mbox{tr }{\bf e}^{S}\right) {\bf 1}+2\mu {\bf e}^{S}+Q\varsigma {\bf 1,}$	(2)
$\displaystyle{\bf T}^{F}$	=	$\displaystyle-\left( M\varsigma +Q\,\mbox{tr }{\bf e}^{S}\right) {\bf 1},$

where ${\bf e}^{S}$ is the Almansi-Hamel tensor of small deformations, $\varsigma$ describes volume changes of the fluid component, $\lambda ,\mu ,M,Q$ are material constants. The constant Q is responsible for interactions introduced to the model by Biot (e.g., [1]).

In the series of papers we show that such a model contradicts basic principles of continuum thermodynamics.

It is a rather easy task to prove that the dynamical contribution with the interaction mass density $\rho _{12}$ violates the principle of material objectivity ([2]). Namely, if we assume that constitutive relations must be invariant with respect to the time-dependent orthogonal transformation in the space of motion $\Re ^{3}$

$\begin{displaymath} {\bf x}^{\ast }={\bf O}\left( t\right) {\bf x}+{\bf d}\left(... ...^{\ast },{\bf x}\in \Re ^{3},\quad {\bf d}\in \mbox{\em V}^{3},\end{displaymath}$ (3)

then a dependence of the diffusive force ${\bf \hat{p}}$ on the relative acceleration $\frac{\partial {\bf v}^{F}}{\partial t}-\frac{\partial {\bf v}^{S}}{\partial t}$ must vanish identically. Consequently, $\rho _{12}$ must be identically zero.

Even if we ignored the principle of material objectivity, contributions of this dynamical interactions would have to be very small. This is also shown in the work [2].

More sophisticated is the argument concerning the coupling constant Q of Biot's model. It is based on the evaluation of the second law of thermodynamics for isothermal processes. Direct substitution of linear constitutive relations in the entropy inequality does not give reliable results because such an evaluation is inconsistent with orders of magnitude of contributions to the inequality. Consequently, one has to rely on the evaluation for the nonlinear model and then one has to make a transition to the linear version with respect to both geometric and kinematical contributions. Such a procedure is not unique and it depends on the structure of a chosen nonlinear model. The following nonlinear models have been investigated ([3, 4]):

1.: A fully nonlinear thermomechanical model of a two-component system with either a balance equation of porosity or a constitutive relation for porosity,
2.: Three hybrid incompressible nonlinear models with either a balance equation of porosity or a constitutive relation for porosity,
3.: A nonlinear model with an incompressible real fluid component, and without a balance equation for porosity.

We present a scheme of argument on the last example.

It is assumed that the mass density of the fluid component $\rho ^{F}$ is related to the real mass density $\rho ^{FR}=const$ by the formula $\rho ^{F}=n\rho ^{FR}$ . Then the partial mass balance equation becomes the equation for the porosity

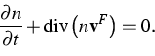$\begin{displaymath} \frac{\partial n}{\partial t}+\mbox{div}\left( n{\bf v}^{F}\right) =0.\end{displaymath}$ (4)

Exploitation of the second law of thermodynamics yields the following constitutive relations for partial stresses

$\displaystyle{\bf T}^{S}$	=	$\displaystyle\lambda \left( tr{\bf e}^{S}\right) {\bf 1}+2\mu {\bf e}^{S}-n_{0}N\varsigma {\bf 1},$	(5)
$\displaystyle{\bf T}^{F}$	=	$\displaystyle-M\varsigma {\bf 1},$

where n₀ denotes a reference porosity, and the constant N appears also as a coefficient in the diffusive force

$\begin{displaymath} {\bf \hat{p}}=\pi \left( {\bf v}^{F}-{\bf v}^{S}\right) +N\mbox{grad}\,n.\end{displaymath}$

(6)

If we consider the model without a constitutive dependence on $\mbox{grad}\, n$ , the constant N is equal to zero and there is no coupling between partial stresses.

Certainly there is no way in which the above relations (5) can be transformed into Biot relations (2). The same conclusion has been proved for all other models. Consequently the classical Biot model seems to be violating two most important conditions of the continuum thermomechanics.

In spite of these flaws practical results which follow from Biot's model seem to be acceptable. This has been checked for numerous problems of practical bearing. As mentioned above the nonobjective contributions are extremally small and cannot be observed in experiments conducted under normal conditions (e.g., on the turntable rotating with angular velocities much smaller than 1 MHz). The influence of Biot's coupling constant Q on the propagation conditions of bulk and surface waves is solely quantitative and there is no change in the number and character of modes of propagation ([5]). The onset of some instabilities such as liquefaction of granular materials is also not influenced by this constant ([6]). The latter arguments seem to advocate the much simpler two-component model developed and investigated in WIAS (e.g., [4]).

References:

M.A. BIOT, D.G. WILLIS, The elastic coefficients of the theory of consolidation, J. Appl. Mech., 24 (1957), pp. 594-601.
K. WILMANSKI, Some questions on material objectivity arising in models of porous materials, in: Rational Continua, Classical and New, M. Brocato, ed., Springer, Italy, 2001, pp. 149-161.
K. WILMANSKI, Mass exchange, diffusion and large deformations of poroelastic materials, in: Modeling and Mechanics of Granular and Porous Materials, G. Capriz, V.N. Ghionna, P. Giovine, eds., Birkhäuser, Basel, 2002, pp. 213-244.
$\dito$ , Thermodynamics of multicomponent continua, in: Earthquake Thermodynamics and Phase Transformations in the Earth's Interior, R. Teisseyre, E. Majewski, eds., International Geophysics Series 76, Academic Press, San Diego, 2001, chapter 25, pp. 567-656.
I. EDELMAN, K. WILMANSKI, Asymptotic analysis of surface waves at vacuum/porous medium and liquid/porous medium interfaces, WIAS Preprint no. 695, 2001, in print in: Contin. Mech. Thermodyn., 14 (2002).
T. WILHELM, K. WILMANSKI, On the onset of flow instabilities in granular media due to porosity inhomogeneities, to appear in: Internat. J. Multiphase Flows.