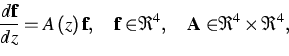
|
|
|
[Contents] | [Index] |
Cooperation with: I. Edelman (Alexander von Humboldt fellow in WIAS, Russian Academy of Sciences, Moscow), C. Lai (Studio Geotecnico Italiano, Milano), S. Foti, R. Lancellotta (Politecnico di Torino, Italy)
Description:
Aims and results of the project
The project is devoted to a theoretical analysis of weak discontinuity waves on the basis of the own model [1], [2], as well as practical geotechnical applications particularly in a nondestructive testing of soils. Three main topics are in the process of investigation:
The first problem is the continuation of the research carried out in the group during the last two years. The analysis of surface waves has been performed primarily in the limit of high frequency which yields the speeds of propagation of impulses ([3]). Such an approximation has the disadvantage of not corresponding to the frequency ranges used in geotechnical applications (approx. 1 to 10 Hz in contrast to some kHZ used in our work). For this reason a new asymptotic approximation has been designed. It seems to give correct results (a preliminary report is due to appear ([4])) but some singularities for different modes of propagation still require an explanation. Let us mention that such singularities (phase speeds going to infinity for low critical frequencies of monochromatic surface waves) appear also in the analysis of classical Rayleigh waves in heterogeneous materials.
The second problem is related to the first one because it concerns surface wave solutions for heterogeneous materials. Under the assumption that material properties depend on the variable z measuring the distance from the surface of the semispace, the wave analysis leads to a differential eigenvalue problem of the following form
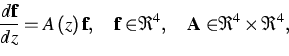 |
(1) |
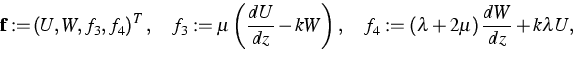
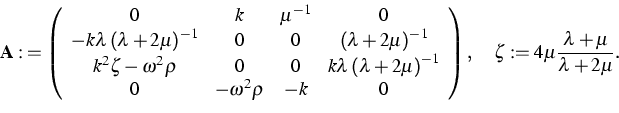 |
(2) |
In order to solve this problem, i.e. in order to find a relation between k
and ![]() , a method of successive approximations has been developed. The
method is based on the assumption that the deviation of the matrix
, a method of successive approximations has been developed. The
method is based on the assumption that the deviation of the matrix ![]() from its average
from its average ![]() with respect to z is a small quantity
with respect to z is a small quantity
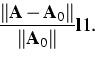 |
(3) |
The third problem is related to a nondestructive testing of soils. It is attempted to develop a systematic acoustic method of in situ measurements of such quantities as the porosity of soils. The first result of this form has been obtained in [5], [6]. It is based on very simple relations between macroscopic material parameters and the porosity. One obtains the following relation between porosity n and the speeds of propagation of the longitudinal P1-wave cP1, the longitudinal P2-wave cP2, and the shear S-wave cS
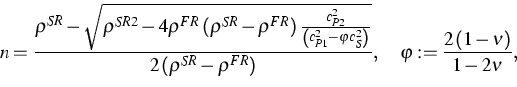 |
(4) |
References:
|
|
|
[Contents] | [Index] |