Nichtisotherme Massenaustauschprozesse in porösen Körpern

[Next]:

Strömungsinstabilitäten und Musterentstehung (Piping) in granularen

[Up]:

Projektbeschreibungen

[Previous]:

Phasenübergänge

[Contents]

[Index]

Nichtisotherme Massenaustauschprozesse in porösen Körpern

Bearbeiter: K. Wilmanski , B. Albers

Kooperation: G. Capriz (Universität Pisa, Italien), P. Giovine (Universität Reggio di Calabria, Italien)

Beschreibung der Forschungsarbeit:

Für ein zweikomponentiges Modell für poröse Körper wurden im Jahr 2000 zwei Fragen untersucht:

1.: Wie sind Wärmefluss und Entropiefluss miteinander gekoppelt, wenn thermische Vorgänge in dem System von einer gemeinsamen absoluten Temperatur $\Theta$ beschrieben werden?
2.: Welche thermischen Eigenschaften besitzt eine durchlässige Trennfläche zwischen porösen Körpern?

Die Antwort wurde für beliebig große Verzerrungen des Skeletts aber für kleine Abweichungen vom thermodynamischen Gleichgewicht gefunden. Wenn ${\bf G}$ den Temperaturgradienten, ${\bf \acute{X}}^{F}$ die Lagrange'sche relative Geschwindigkeit der Komponenten und $\Delta =n-n_{E}$ die Abweichung der Porosität n vom Gleichgewichtswert n_E bezeichnen, dann ist die Dissipation D im System durch die folgende Beziehung definiert

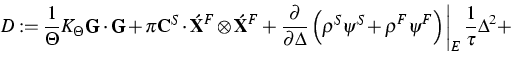
$\begin{displaymath} D:=\frac{1}{\Theta }K_{\Theta }{\bf G\cdot G}+\pi {\bf C}^{S... ...F}\psi ^{F}\right) \right\vert _{E}\frac{1}{\tau }\Delta ^{2}+ \end{displaymath}$

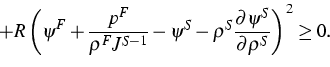
$\begin{displaymath} +R\left( \psi ^{F}+\frac{p^{F}}{\rho ^{F}J^{S-1}}-\psi ^{S}-... ...rac{\partial \psi ^{S}}{\partial \rho ^{S}}\right) ^{2}\geq 0. \end{displaymath}$

$K_{\Theta }$ ist die gemeinsame Wärmeleitfähigkeit der Komponenten, $\pi$ bezeichnet die Permeabilität, $\tau$ ist die Porositäts-Relaxationszeit, und es sind R die Massenaustauschkonstante, $\psi ^{S},\psi ^{F}$ partielle Helmholtz'sche freie Energien, p^F der partielle Druck der Flüssigkeit, $\rho ^{S},\rho ^{F}$ partielle Massendichten, ${\bf C}^{S}$ der Cauchy-Green-Deformationstensor und $J^{S}=\sqrt{\det {\bf C}^{S}}.$ Der thermodynamische Gleichgewichtszustand ist durch die Beziehung D=0 definiert.

Unter der Voraussetzung einer kleinen Abweichung vom Zustand D=0 wurde bewiesen, dass die partiellen Flüsse der folgenden Beziehung genügen

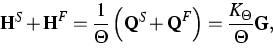
$\begin{displaymath} {\bf H}^{S}+{\bf H}^{F}=\frac{1}{\Theta }\left( {\bf Q}^{S}+{\bf Q}^{F}\right) =\frac{K_{\Theta }}{\Theta }{\bf G,} \end{displaymath}$

wobei ${\bf H}^{S},{\bf H}^{F}$ intrinsische partielle Entropieflüsse und ${\bf Q}^{S},{\bf Q}^{F}$ intrinsische partielle Wärmeflüsse bezeichnen.

Der Porositätsfluss hat die Gestalt

$\begin{displaymath} {\bf J}=\varphi J^{S}{\bf \acute{X}}^{F}, \end{displaymath}$

wobei $\varphi$ nur von der Anfangsporosität abhängig ist.

Auch alle anderen Stoffgesetze wurden vollständig spezifiziert.

Auf den Trennflächen gilt die Kontinuität der absoluten Temperatur $\Theta$ , was bedeutet, dass die Temperatur eine messbare Größe ist. Dieses Ergebnis wurde für mehrkomponentige Systeme zum ersten Mal streng bewiesen. Es enthält Bedingungen, die erfüllt sein müssen, wenn man die klassische Wärmeleittheorie in Modellen für poröse Körper verwenden will.

Die Arbeit wurde auch teilweise dem Problem von Oberflächenkompatibilitätsbedingungen gewidmet. Auf diese Weise wurde die Anfangsrandwertaufgabe nun vollständig formuliert.

Unter den oben genannten Bedingungen kann man Randwertprobleme für nichtisotherme Massenaustauschprozesse untersuchen. Diese Ergänzung von eigenen Arbeiten über Adsorptionsvorgänge ist Ziel der nachfolgenden Arbeit.

Projektliteratur:

K. WILMA´NSKI, Mathematical theory of porous media -- lecture notes, WIAS-Preprint No. 602, 2000.
$\dito$ , Mass exchange, diffusion and large deformations of poroelastic materials, WIAS-Preprint No. 628, 2000, erscheint in: Mathematical Models in Soil Mechanics (G. Capriz, P. Giovine, Hrsg.), Birkhäuser, 2001.