[Next]:  Normalformen für homokline Bifurkationen  
 [Up]:  Projektbeschreibungen  
 [Previous]:  Projektbeschreibungen  
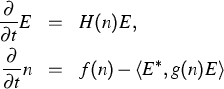
 [Contents]   [Index] 

Dynamik von Halbleiterlasern

Bearbeiter: M. Radziunas , K. R. Schneider , J. Sieber , D. Turaev , M. Wolfrum  

Kooperation: B. Sartorius, D. Hoffmann, H.-P. Nolting, O. Brox (Heinrich-Hertz-Institut für Nachrichtentechnik, Berlin), H.-J. Wünsche (Institut für Physik, Humboldt-Universität zu Berlin), V. Tronciu (Technische Universität Moldawien), L. Recke (Institut für Mathematik, Humboldt-Universität zu Berlin), H. Wenzel (Ferdinand-Braun-Institut für Höchstfrequenztechnik, Berlin)

Beschreibung der Forschungsarbeit:

Moderne optoelektronische Bauelemente, wie z. B. Mehrsektionslaser, Laser mit Rückkopplung oder periodischer Modulation, zeigen oft ein kompliziertes raum-zeitliches dynamisches Verhalten. Die Untersuchung von solchen nichtlinearen Effekten macht die Verwendung und Weiterentwicklung von Methoden der nichtlinearen Dynamik sowie die Entwicklung von speziellen numerischen Verfahren notwendig. Das bearbeitete Spektrum von Aufgabenstellungen reicht von der problemangepassten Modellierung über grundlegende analytische Eigenschaften der entsprechenden Modelle bis zur Entwicklung und Optimierung konkreter Bauelemente zur optischen Datenverarbeitung (hochfrequente Pulsationen und Schalteffekte, Signalregeneration) in Zusammenarbeit mit den Kooperationspartnern. Diese Technologie der rein optischen Datenverarbeitung soll in zukünftigen Datennetzen wesentlich höhere Übertragungsraten ermöglichen.

Mit dem Programmpaket LDSL-Tool steht mittlerweile eine Software zur Verfügung, mit der für eine große Klasse von kantenemittierenden Laser-Bauelementen Simulationen von Anfangswertaufgaben und die Berechnung von spektralen Eigenschaften des optischen Operators durchgeführt werden können ([3]). Dafür stehen inzwischen auch Algorithmen zur Berücksichtigung zusätzlicher physikalischer Effekte (z. B. nichtlineare Gain-Dispersion) und spezieller experimenteller Situationen (z. B. externe Anregung durch ein Datensignal) zur Verfügung.

Die Dynamik eines Halbleiterlasers wird in vielen Fällen durch ein System von Gleichungen der Form

\parbox {13cm}{ \begin{eqnarray*} \frac{\partial}{\partial t}E & = & H(n)E,\ \frac{\partial}{\partial t}n & = & f(n) - \langle E^*,g(n)E \rangle\end{eqnarray*}}   % latex2html id marker 2150 \parbox {1cm}{\begin{eqnarray}\end{eqnarray}}

beschrieben, wobei E für das komplexe elektrische Feld und n für die Ladungsträger stehen. Je nach der konkreten Situation kann dabei E ein endlichdimensionaler Vektor oder auch eine mehrkomponentige, räumlich aufgelöste Funktion sein. Im letzteren Fall ist der lineare Operator H(n) dann typischerweise ein hyperbolischer Differentialoperator, der die Wellenausbreitung, Lichtverstärkung und eine Brechung am Bragg-Gitter beschreibt. Die Ladungsträgerdichten n können dabei sowohl räumlich aufgelöst als auch gemittelt über die einzelnen Sektionen des Lasers betrachtet werden. Dem komplizierten Verhalten dieser Modelle liegen einerseits die nichtlineare Kopplung zwischen Ladungsträgerdichten und elektrischem Feld sowie andererseits die unterschiedlichen Zeitskalen in der Evolution von Elektronen und Photonen zugrunde.

Nichtlineare Gain-Dispersion   (Bearbeiter: J. Sieber, M. Wolfrum, M. Radziunas).

Um eine exaktere Übereinstimmung von Modellrechnungen und experimentellen Ergebnissen zu erzielen, wurde mit der nichtlinearen Polarisation des Materials ein weiterer physikalischer Effekt in das bekannte Travelling-Wave-Modell miteinbezogen, der zu einer nichtlinearen Gain-Dispersion führt. Dabei wird das Feld E neben den zwei Amplituden $\Psi^+(z,t)$ und $\Psi^-(z,t)$ für die vorwärts und rückwärts laufenden optischen Wellen noch durch zwei Amplituden P+(z,t) und P-(z,t) für die Polarisation beschrieben. Dies führt auf ein weiteres Paar von Gleichungen oder, äquivalent dazu, zu einem zeitlich nichtlokalen Term in der Gleichung für die optischen Amplituden.

Für das erweiterte Modell wurden Existenz und Eindeutigkeit der Lösung sowie die spektralen Eigenschaften des Feldoperators untersucht ([2], [6]).

Obwohl die Polarisation im vorliegenden Fall nur eine kleine Störung des Ausgangssystems bewirkt, konnte gezeigt werden, dass dadurch Änderungen in der Modenselektivität hervorgerufen werden, die unter bestimmten Bedingungen zu erheblichen Änderungen im Langzeitverhalten führen können ([2]). Simulationsrechnungen mit dem erweiterten Modell zeigen für praxisrelevante Situationen erhebliche Unterschiede der berechneten Pulsationsgebiete (s. Abb. 1).


 
Abb. 1:   Links: Reflektivität der aktiven DFB-Sektion und Materialdispersion (gestrichelt: nichtlineare Dispersionskurve, gepunktet: konstante Dispersion, d. h. ohne Berücksichtigung von Polarisation). Rechts: maximale und minimale Ausgangsleistung in Abhängigkeit des Phasenparameters $\delta$ (blau: wachsendes $\delta$, rot: fallendes $\delta$) und Pulsationsgebiete ohne Hysterese (violette Region).
\ProjektEPSbildNocap {0.7\textwidth}{fig2_mr_1.eps}

Modenapproximationen   als genäherte invariante Mannigfaltigkeiten (Bearbeiter: J. Sieber).

Bei der Untersuchung der Dynamik von Halbleiterlasern mit dispersiver Rückkopplung wird mit einer Hierarchie von Modellen gearbeitet. Darunter verstehen wir einerseits Systeme von partiellen und gewöhnlichen Differentialgleichungen, also unendlich-dimensionale dynamische Systeme, die zur Simulation und Optimierung von Bauelementen verwendet werden. Hierbei handelt es sich um numerische Untersuchungen über einen kleinen Zeithorizont. Zur Untersuchung spezieller nichtlinearer Effekte (z. B. Bifurkationsszenarios) werden niedrigdimensionale Systeme gewöhnlicher Differentialgleichungen verwendet, die einer Langzeit- sowie Bifurkationsanalyse leichter zugänglich sind.

Für diese Zwecke wurden von Physikern rein heuristisch die niedrigdimensionalen Modenapproximationen von (1) hergeleitet. Ein wichtiger Schritt zum Verständnis der verwendeten Modellhierarchie ist die mathematische Rechtfertigung dieser Modellreduktion.

Ein wesentlicher Fakt, der bei der Modellreduktion eine wichtige Rolle spielt, besteht darin, dass das optische Feld E und die Ladungsträgerdichte n auf unterschiedlichen Zeitskalen operieren, wobei n die langsame Variable ist. Unter diesem Gesichtspunkt kann System (1) als ein singulär gestörtes System betrachtet werden.

In [9] wird (1) als System gewöhnlicher Differentialgleichungen betrachtet. Es wird bewiesen, dass unter bestimmten Voraussetzungen über H(n) dieses System für kleine $\varepsilon$ eine exponentiell attrahierende invariante Mannigfaltigkeit besitzt, die alle beschränkten Orbits enthält. Demnach kann mit einer geringen Anzahl von Moden von E die Dynamik präzise beschrieben werden. In der Arbeit werden Ein-Moden- und Zwei-Moden-Modelle mit einer einzigen optischen Frequenz analysiert. Insbesondere wird gezeigt, dass das Parametergebiet mit Selbstpulsationen relativ klein ist.

In [6] ist gezeigt worden, dass die klassischen Aussagen über die Existenz, Attraktivität und asymptotische Entwickelbarkeit invarianter Zentrumsmannigfaltigkeiten für Systeme gewöhnlicher Differentialgleichungen auch für die partielle Differentialgleichung (1) gelten. Wesentlicher Grund dafür sind die spektralen Eigenschaften des Operators H in (1).

In diesem Sinn sind die Modenmodelle eine Approximation erster Ordnung der Zentrumsmannigfaltigkeiten. Dieses Einbettungsresultat erlaubt es, sämtliche für die Modenapproximationen gewonnenen Erkenntnisse auf (1) zu übertragen, so lange sie robust gegenüber regulären Störungen sind (Aussagen über die Existenz von Selbstpulsationen, ihre dynamische Stabilität, stetige Abhängigkeit von Parametern, Synchronisationseigenschaften, generische Bifurkationsszenarios etc.) ([6]).

Bifurkationsanalyse   der Zwei-Moden-Approximation (Bearbeiter: J. Sieber, D. Turaev).

In Simulationen von (1) tritt häufig der Fall auf, dass zwei Moden von H mit sehr verschiedener Frequenz nahezu gleich stark unterstützt werden (eine typische Eigenschaft von DFB-Lasern). Nach Übergang zur Zwei-Moden-Approximation erhält man ein fünfdimensionales System gewöhnlicher Differentialgleichungen. Der große Frequenzunterschied bewirkt jedoch, dass die Phasendifferenz zwischen den Moden so schnell rotiert, dass sie sich in erster Ordnung herausmittelt. Nach dieser Mittelung kann, ausgehend von den Ergebnissen über die Dynamik der Ein-Moden-Approximation ([1]), die Modenkonkurrenz oder -kooperation dynamisch (d. h. 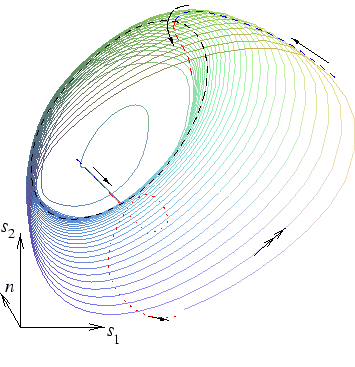nicht nur in der Nähe von stationären Zuständen) in einem dreidimensionalen System analysiert werden. Im Fall der Modenkooperation ist dabei ein in diesen Modellen neuartiger Typ von stabiler raum-zeitlicher Dynamik gefunden worden: ein langsames Hin- und Herdriften zwischen zweimodiger Schwebung und einmodiger Selbstpulsation (siehe Abb. 2).

 
Abb. 2:   ,,Bursting``-Lösung im gemittelten Zwei-Moden-Modell mit einer aktiven Sektion. Dieser Typ von Lösungen wird häufig in Neuronenmodellen gefunden.
\ProjektEPSbildNocap {0.5\textwidth}{fig2_js_1.eps}

Erregbarkeit   von Lasern mit passivem dispersivem Reflektor (Bearbeiter: K. R. Schneider, J. Sieber).

Im Rahmen der rein optischen Signalübertragung spielt neben dem Bauelement, das auf die Modulationsfrequenz einlockt, das so genannte Entscheiderelement eine grundlegende Rolle. Es hat die Aufgabe, für jedes eingehende Signal zu entscheiden, ob es ein Störsignal ist (Rauschen) oder ein Informationssignal darstellt.

Eine ähnliche Funktion besitzen die Neuronen. Ihre charakteristischen Eigenschaften sind:

(i)
Es existiert eine Reizschwelle. Alle unterschwelligen Reize bewirken nur eine lokale Antwort, die nicht weitergeleitet wird.
(ii)
Alle überschwelligen Reize führen zu einem schnellen charakteristischen Anwachsen und Abfallen des Aktionspotentials (Spikes). Die Form der Spikes hängt nicht von der Stärke des überschwelligen Reizes ab.
(iii)
Wirken auf ein Neuron zwei aufeinanderfolgende überschwellige Reize ein, dann treten nur dann zwei Spikes auf, wenn der zeitliche Abstand der aufeinanderfolgenden Reize eine charakteristische Zeit (Refraktärperiode) nicht unterschreitet.
Die Eigenschaften (i)-(iii) werden als Erregbarkeit bezeichnet. In jüngster Vergangenheit wurde auch an Lasermodellen Erregbarkeit beobachtet (optische Kavitäten, Laser mit sättigbaren Absorbern und Halbleiterlaser mit verzögertem optischen Feedback).

Unser Ziel besteht darin, Erregbarkeit bei Halbleiterlasern mit dispersiver Rückkopplung nachzuweisen. Im ersten Schritt auf diesem Weg verwenden wir ein Ein-Moden-Modell, das einen Laser mit einer Lasersektion und einem passiven dispersiven Reflektor beschreibt. Die Modellgleichungen lauten

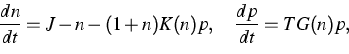
\begin{displaymath} \frac{dn}{dt} =J-n-(1+n)K(n)p, \quad \frac{dp}{dt} = T G(n)p,\end{displaymath}

wobei n die Ladungsträgerdichte und p die Photonendichte in der Lasersektion beschreibt. J ist der an der Lasersektion angelegte Strom, die Funktion K(n) ist die Petermann-Funktion, die wie folgt dargestellt wird

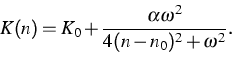
\begin{displaymath} K(n) = K_0 + \frac{\alpha \omega^2}{4(n-n_0)^2 + \omega^2}.\end{displaymath}

Der Parameter n0 beschreibt die Stelle, an der K(n) eine Resonanz besitzt. Die Applikation der Störungen (Reize) erfolgt über den Strom J in Form von Rechteck-Impulsen. Die folgenden Abbildungen zeigen, dass derartige Lasermodelle Erregbarkeit aufweisen. In Zukunft sollen die zugrunde liegenden Erregungsszenarios in Verbindung mit dem Phasenportrait untersucht werden.


 
Abb. 3:   Schwellenverhalten. Linke Abbildung: unterschwellige Störung führt zur Nichts-Antwort, überschwellige Störung führt zur Alles-Antwort (Spike).

Rechte Abbildung: sprunghafter Anstieg der Antwort an der Reizschwelle.
\ProjektEPSbildNocap {1.0\textwidth}{fig2_ks_exit.eps}


 
Abb. 4:   Refraktärperiode: a) Spike auf überschwellige Störung, b) zweite überschwellige Störung während der Refraktärperiode (1 Spike), c) zweite überschwellige Störung nach der Refraktärperiode (2 Spikes).
\ProjektEPSbildNocap {0.9\textwidth}{fig2_ks_6.eps}

Simulation von mehrmodigen hochfrequenten Selbstpulsationen:   (Bearbeiter: M. Rad-
ziunas).

Hochfrequente Selbstpulsationen, die mit einem eingestrahlten Datensignal synchronisieren, spielen eine zentrale Rolle bei der Taktrückgewinnung zur rein optischen Signalregeneration. In früheren Arbeiten ([5]) wurden in Zusammenarbeit mit dem Heinrich-Hertz-Institut 3-Sektions-Laser mit einer aktiven und zwei passiven Sektionen untersucht. Diese zeigen so genannte DQS-Pulsationen im Bereich von 5 bis 20 GHz und können mit einem externen Signal synchronisieren. Diese Pulsationen treten typischerweise nur in kleinen Gebieten im Parameterraum auf und bedürfen daher einer sorgfältigen Abstimmung.

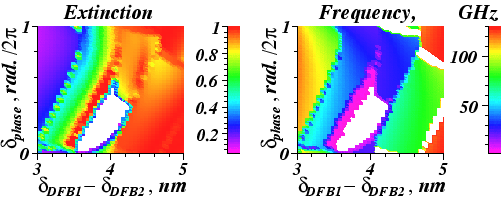
In [4] wurden erstmals sowohl experimentelle als auch numerische Ergebnisse vorgestellt, bei denen Frequenzen von 40 - 100 GHz und deren Synchronisation gezeigt werden konnten. Dies wurde erreicht durch ein verändertes Design der Bauelemente, die hier aus zwei aktiven DFB-Sektionen und einer dazwischen liegenden passiven Phasensektion bestehen.

Es konnte gezeigt werden, dass diese Pulsationen auf einem grundlegend anderen Mechanismus beruhen und in großen Gebieten im Parameterraum auftreten. Anhand von Simulationsrechnungen konnten wesentliche Erkenntnisse zur Optimierung hinsichtlich von Modulationstiefe, Frequenz und Synchronisationsverhalten gewonnen werden.

 


 
Abb. 5:  Modulationstiefe (Pmax-Pmin)/(Pmax+Pmin) und Frequenz von zweimodigen Pulsationen für verschiedene Werte von Phasen- und Detuning-Parameter.
\ProjektEPSbildNocap {0.7\textwidth}{fig2_mr_3.eps}

Projektliteratur:

  1.   U. BANDELOW, M. RADZIUNAS, V. TRONCIU, H.-J. WÜNSCHE, F. HENNEBERGER, Tailoring the dynamics of diode lasers by dispersive reflectors, in: ,,Physics and Simulation of Optoelectronic Devices VIII`` (R. H. Binder, P. Blood, M. Osinski, Hrsg.), Proceedings of SPIE, 3944, SPIE, Bellingham, WA, 2000, pp. 536-545.
  2.   U. BANDELOW, M. RADZIUNAS, J. SIEBER, M. WOLFRUM, Impact of gain dispersion on the spatio-temporal dynamics of multisection lasers, WIAS-Preprint No. 597 , 2000, erscheint in: IEEE J. Quantum Electronics, Februar 2001.
  3.   M. RADZIUNAS, H.-J. WÜNSCHE, B. SARTORIUS, O. BROX, D. HOFFMANN, K. SCHNEIDER, D. MARCENAC, Modeling self-pulsating DFB lasers with an integrated phase tuning section, IEEE J. Quantum Electronics, 36 (2000), pp. 1026-1034.
  4.   M. MÖHRLE, B. SARTORIUS, C. BORNHOLDT, S. BAUER, O. BROX, A. SIGMUND, R. STEINGRÜBER, M. RADZIUNAS, H.-J. WÜNSCHE, Detuned grating multi-section-RW-DFB-lasers for high speed optical signal processing, eingereicht.
  5.   M. RADZIUNAS, K. SCHNEIDER, J. SIEBER, D. TURAEV, M. WOLFRUM, Nonlinear dynamics of semiconductor lasers, Poster, 3rd International Symposium ,,Investigation of Nonlinear Dynamic Effects in Production Systems``, Brandenburgische Technische Universität Cottbus, 26. - 27. September 2000.
  6.   J. SIEBER, Dynamics in a longitudinal semiconductor laser model, Dissertation, eingereicht bei der Humboldt-Universität zu Berlin.
  7.   V. Z. TRONCIU, H.-J. WÜNSCHE, M. RADZIUNAS, K. SCHNEIDER, Excitability of laser with integrated dispersive reflectors, erscheint in: SPIE Proceedings Series, 2001.
  8.   V. Z. TRONCIU, H.-J. WÜNSCHE, J. SIEBER, K. SCHNEIDER, F. HENNEBERGER, Dynamics of single mode semiconductor lasers with passive dispersive reflectors, Optics Communications, 182 (2000), pp. 221-228.
  9.  D. TURAEV, Fundamental obstacles to self-pulsations in low-intensity lasers, WIAS-Preprint, in Vorbereitung.


 [Next]:  Normalformen für homokline Bifurkationen  
 [Up]:  Projektbeschreibungen  
 [Previous]:  Projektbeschreibungen  
 [Contents]   [Index] 

LaTeX typesetting by I. Bremer
4/30/2001