Mathematische Modellierung von Hysteresephänomenen

[Next]:

Existenz und Optimierung nichtglatter mechanischer Strukturen

[Up]:

Projektbeschreibungen

[Previous]:

Modellierung und Simulation von hochsperrenden Bauelementen

[Contents]

[Index]

Mathematische Modellierung von Hysteresephänomenen

Bearbeiter: P. Krejcí , M. Siegfanz , J. Sprekels

Kooperation: J. Francu (Technische Universität Brno, Tschechische Republik), K. Kuhnen (Universität des Saarlandes, Saarbrücken), Ph. Laurençot (CNRS & Universität Nancy/Universität Toulouse, Frankreich), A. Vladimirov (Institut für Informationsübertragung Moskau, Russland)

Beschreibung der Forschungsarbeit: Die Theorie der Hystereseoperatoren stellt einen erfolgreichen Zugang dar zu der Modellierung der Hysteresephänomene in der Elastoplastizität, Piezoelektrizität, Phasenumwandlungen oder im Ferromagnetismus. Dieses Forschungsgebiet entwickelt sich aktiv sowohl in der theoretischen Richtung wie in Anwendungen. Typischerweise beziehen sich Hystereseoperatoren, die in der Praxis am häufigsten verwendet werden, direkt oder indirekt auf die Variationsungleichung

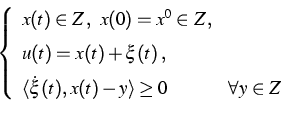$\begin{displaymath} \left\{ \begin{array} {ll} x(t) \in Z\, , \ x(0) = x^0 \in Z... ... x(t) - y\rangle \ge 0\, \ &\forall y \in Z\,\end{array}\right.\end{displaymath}$ (1)

im entsprechenden Sinn mit einer gegebenen Funktion $u: [0,T] \to X$ , wobei X ein Hilbertraum mit Skalarprodukt $\langle \cdot, \cdot \rangle$ und Z eine konvexe abgeschlossene Menge sind und $\dot \xi$ die Ableitung der gesuchten Funktion $\xi$ nach t bezeichnet. Wenn u absolutstetig ist, hat die Variationsungleichung (1) eine eindeutige absolutstetige Lösung und ist fast überall erfüllt. Der Lösungsoperator $(u, x^0) \mapsto \xi$ heißt dann Play mit Charakteristik Z. Ist das Innere von Z nicht leer, kann der Play-Operator auf den ganzen Raum der stetigen Funktionen erweitert werden.

a) Im Rahmen des Projektes wurden weitere Eigenschaften des Play-Operators untersucht. Die Arbeit [4] zeigt, dass die $W^{2,\infty}$ -Regularität des Randes $\partial Z$ nicht nur hinreichend für die Lipschitz-Stetigkeit des Play-Operators in W^1,1 ist, sondern auch notwendig. In [10] wird der Play-Operator stetig auf den Raum der Regelfunktionen (d. h. Funktionen, die in jedem Punkt beide einseitige Grenzwerte besitzen) erweitert. Dabei muss die Variationsungleichung (1) mit Hilfe des Young-Integrals in der Form umgeschrieben werden

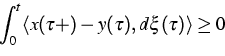$\begin{displaymath} \int_0^t \langle x(\tau+) - y(\tau), d\xi(\tau)\rangle \ge 0\end{displaymath}$ (2)

für jedes $t \in [0,T]$ und jede Regelfunktion $y : [0,T] \to Z$ . Im skalaren Fall ist es in [9] gelungen, den Play-Operator sogar stetig auf den Raum $L^\infty$ zu erweitern. Dabei wird die Variationsungleichung (1) durch das Prinzip der minimalen Variation ersetzt.

Die Variationsungleichung (1) kann, auch wenn Z ein Polyeder ist, als ein Spezialfall des Skorokhod-Problems aus der Theorie der Warteschlangen interpretiert werden. Hinreichende Bedingungen für die Lipschitz-Stetigkeit des Skorokhod-Operators im Raum der stetigen und absolutstetigen Funktionen wurden in [6] als geometrische Bedingungen zwischen den Normalenvektoren und Reflexionsvektoren formuliert. Diese Bedingungen sind automatisch erfüllt, wenn die Normalen- und Reflexionsvektoren identisch sind, und in diesem Fall ist das Skorokhod-Problem äquivalent der Variationsungleichung (1).

b) Als Anwendung der Hystereseoperatoren zur Beschreibung zeitabhängiger Prozesse im Ferromagnetismus wurde das asymptotische Verhalten der Lösung einer Differentialgleichung zweiter Ordnung mit einem Preisach-Operator in den Arbeiten [2, 3] als Modell für einen Schwingungskreis mit ferromagnetischer Induktanz untersucht. Das Ergebnis besteht in einer expliziten Gleichgewichtsbedingung zwischen der Energiezufuhr und der Hysterese-Energiedissipation, die eine unbeschränkte Resonanz verhindert.

Zusammen mit Ingenieuren der Universität des Saarlandes in Saarbrücken wurde das Problem der Echtzeitsteuerung eines magnetostriktiven oder piezoelektrischen Aktors als das mathematische Problem der Invertierbarkeit der Kombination eines Prandtl-Ishlinskii-Operators mit einem Kriechoperator umformuliert. Der Beweis der Lipschitz-Stetigkeit des Inversen Operators wurde in [7] zur Formulierung eines konvergenten numerischen Verfahrens ausgenutzt.

Ein thermodynamisch konsistentes Modell für die temperaturabhängige magnetische Nachwirkung wurde in [8] als eine Erweiterung des Preisach-Modells der ferromagnetischen Hysterese vorgeschlagen. Die Korrektheit des Modells wurde im ganzen Temperaturbereich bewiesen.

c) Der dritte untersuchte Themenkreis hängt mit der Modellierung der Elastoplastizität und Thermoelastoplastizität zusammen. Die Arbeit [1] fasst bisherige Ergebnisse der Autoren über die Modellierung der Thermoelastoplastizität mit Hilfe von temperaturabhängigen Prandtl-Ishlinskii-Hystereseoperatoren zusammen. Impuls- und Energiebilanz haben im eindimensionalen Fall die Form

$\begin{eqnarray} \varrho\,u_{tt} &=& \sigma_x + f(\theta, x, t)\, ,\ [1mm]\nonu... ...\sigma&=& {\cal P} [u_x, \theta] + \mu\,u_{xt} - \beta\,\theta\, ,\end{eqnarray}$

wobei u die Verschiebung, $\sigma$ die Spannung, $\theta$ die absolute Temperatur, f die äußere Kraft, g die Wärmequelle, ${\cal P}$ der temperaturabhängige Prandtl-Ishlinskii-konstitutive Operator zur Modellierung eines thermoelastoplastischen Materialgesetzes, ${\cal V}$ das Prandtl-Ishlinskii-Hysteresepotential ist und $c_V\,,\, \kappa\,,\, \mu\,,\, \beta$ positive Konstanten sind. Existenz, Eindeutigkeit und asymptotisches Verhalten der Lösung gehören zu den wichtigsten Ergebnissen in diesem Fall.

Weitere Ergebnisse wurden im temperaturunabhängigen Fall ohne Viskosität erzielt. Für die entsprechende Gleichung

$\begin{displaymath} \varrho\,u_{tt} = {\cal P} [u_x]_x + f(x, t)\end{displaymath}$ (3)

mit verschiedenen Randbedingungen wurde in [11] ein konvergentes numerisches Schema zur Approximation der starken Lösung der Anfangsrandwertaufgabe zusammen mit effizienten Fehlerabschätzungen entwickelt.

Die Arbeit [5] ist dem Homogenisierungsproblem für eine Gleichung vom Typ (4) gewidmet, die als ein Modell für einen oszillierenden nichthomogenen elastisch-plastischen Stab interpretiert werden kann. Das Materialgesetz hat die Form eines raumabhängigen Prandtl-Ishlinskii-Operators ${\cal P} [x, u_x]$ , und die Massendichte $\varrho$ hängt auch von x ab.

Projektliteratur:

P. KREJCÍ , J. SPREKELS, A thermodynamically consistent hysteresis model of thermovisco-elastoplasticity, in: Anniversary Volume for Krzysztof Wilmanski, WIAS-Report No. 18, 2000, pp. 138-145.
P. KREJCÍ, Forced oscillations in Preisach systems, Phys. B, 275 (2000), pp. 81-86.
$\dito$ ,Resonance in Preisach systems, Appl. Math., 45 (2000), No. 6, pp. 439-468.
$\dito$ ,A remark on the local Lipschitz continuity of vector hysteresis operators, Appl. Math., im Druck.
J. FRANCU, P. KREJCÍ, Homogenization of scalar wave equation with hysteresis operator, in: EQUADIFF 99 -- Proceedings of the International Conference on Differential Equations, Berlin 1999 (B. Fiedler, K. Gröger, J. Sprekels, Hrsg.), 2, World Scientific, Singapore [u. a.], 2000, pp. 363-368.
P. KREJCÍ , A.A. VLADIMIROV, Lipschitz continuity of polyhedral Skorokhod maps, WIAS-Preprint No. 566, 2000, eingereicht.
P. KREJCÍ , K. KUHNEN, Inverse control of systems with hysteresis and creep, eingereicht.
P. KREJCÍ, A model for a Preisach-type aftereffect, eingereicht.
P. KREJCÍ , P. LAURENçOT, Hysteresis filtering in the space of bounded measurable functions, WIAS-Preprint No. 608, 2000, eingereicht.
$\dito$ ,Generalized variational inequalities, in Vorbereitung.
M. SIEGFANZ, Die eindimensionale Wellengleichung mit Hysterese, Dissertation, Humboldt-Universität zu Berlin, 2000.