Stochastische Partikelsysteme als numerische Verfahren für

[Next]:

Forschungsgruppe Stochastische Algorithmen und Nichtparametrische Statistik

[Up]:

Tieftemperaturphasen in Modellen mit langreichweitiger Wechselwirkung

[Previous]:

Effektive Steuerung von stochastischen Partikelverfahren für

[Contents]

[Index]

Stochastische Partikelsysteme als numerische Verfahren für Probleme der Aerosoldynamik

Bearbeiter: W. Wagner , A. Eibeck

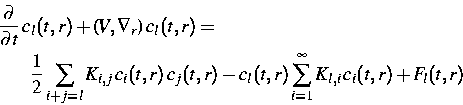
Kooperation: H. Babovsky (Technische Hochschule Ilmenau), A. Kolodko (Institut für Numerische Mathematik, Novosibirsk, Russland), K. Sabelfeld (FG 6)

Förderung: DFG-Schwerpunktprogramm ,,Interagierende Stochastische Systeme von hoher Komplexität``

Beschreibung der Forschungsarbeit: Das physikalische Phänomen der Koagulation, d. h. der Prozess der Bildung von Teilchen unterschiedlicher Größe aus Monomeren durch entsprechende Wechselwirkung, spielt in vielen Anwendungsbereichen, wie etwa der Aerosoltechnologie und der Umweltforschung, eine wichtige Rolle. Zur mathematischen Beschreibung dieses Vorgangs wird die Smoluchowski-Gleichung

$\begin{eqnarray} \lefteqn{ \frac{\partial}{\partial t}\, c_l(t,r) + \mbox{\bf{... ... c_l(t,r)\sum_{i=1}^{\infty} K_{l,i}\,c_i(t,r) + F_l(t,r)\nonumber\end{eqnarray}$

benutzt. Die Lösung c_l(t,r) entspricht der Konzentration von Teilchen der Größe $l=1,2,\ldots$ am Ort r zur Zeit $t\,.$ Weiterhin bezeichnet V die Geschwindigkeit des Trägermediums, K den Koagulationskern und F_l(t,r) einen Quellterm für Teilchen der Größe $l\,.$

Das Forschungsprojekt befasst sich mit der Untersuchung des Zusammenhangs zwischen stochastischen wechselwirkenden Teilchensystemen und Lösungen von Gleichungen des Typs (1). Zum einen führen dabei Ergebnisse über das asymptotische Verhalten der stochastischen Systeme (bei wachsender Teilchenzahl) zu Aussagen über Eigenschaften der Lösung. Zum anderen können geeignete stochastische Systeme zur Entwicklung von Partikelverfahren zur numerischen Behandlung der makroskopischen Gleichung benutzt werden.

In wichtigen Anwendungsbereichen, wie etwa dem Schadstofftransport in der Atmosphäre, finden Transport und Koagulation der Teilchen in einer turbulenten Strömung statt. Dabei wird das Trägermedium durch ein zufälliges Geschwindigkeitsfeld V in der Gleichung (1) charakterisiert. In der Arbeit [1] wurden Untersuchungen zur Behandlung des räumlich inhomogenen Falls durchgeführt. Anhand numerischer Experimente wurde der Einfluss des zufälligen Mediums auf wichtige Charakteristika des Koagulationsprozesses, wie mittlere Teilchenanzahl oder Größenverteilung der Teilchen, untersucht.

In der Arbeit [2] wurde eine neue Klasse stochastischer Algorithmen zur numerischen Behandlung der räumlich homogenen Koagulationsgleichung entwickelt. Diese Verfahren basieren auf der Einführung einer geeigneten fiktiven Wechselwirkung sowie auf Techniken zur effizienten Modellierung der dabei entstehenden Wahrscheinlichkeitsverteilungen. Die mathematische Fundierung der Algorithmen basiert auf den im Vorjahr gewonnenen Konvergenzresultaten.

Ein bei stark wachsenden Koagulationsraten K auftretendes Phänomen von sowohl theoretischem als auch praktischem Interesse stellt die Gelation dar. Im Rahmen der analytischen Beschreibung durch die Gleichung (1) wird dieser Effekt durch einen Masseverlust der Lösung widergespiegelt. Eine entsprechende Interpretation in der Sprache der stochastischen Teilchensysteme ist die Bildung sehr großer Teilchen (proportional zur Größe des Gesamtsystems) in endlicher Zeit. Mittels der oben beschriebenen stochastischen Algorithmen wurde es ermöglicht, den Gelationseffekt für unterschiedliche Kerne quantitativ zu untersuchen.

Projektliteratur:

A. KOLODKO, K. SABELFELD, W. WAGNER, A stochastic method for solving Smoluchowski's coagulation equation, Math. Comput. Simulation, 49 (1999), No. 1-2, pp. 57-79.
A. EIBECK, W. WAGNER, An efficient stochastic algorithm for studying coagulation dynamics and gelation phenomena, WIAS-Preprint No. 473, 1999.