Bearbeiter: A. Glitzky
,
R. Hünlich
Kooperation: W. Merz (Technische Universität München)
Förderung: DFG: ,,Analytische Untersuchungen von
Elektro-Reaktions-Diffusionsgleichungen mit nichtglatten Daten``
Beschreibung der Forschungsarbeit:
Die im vergangenen Jahr begonnenen Untersuchungen zu
Paardiffusionsmodellen
(vgl. [3]) wurden fortgesetzt,
wobei jetzt auch spezielle Fälle von
Heterostrukturen diskutiert wurden.
Wir betrachten m Spezies Xi, von denen nur die ersten
l als diffundierend angenommen werden, und bezeichnen mit  das
chemische Potential der Elektronen,
das
chemische Potential der Elektronen,  sind geeignet gewählte
vom Ort und von
sind geeignet gewählte
vom Ort und von  abhängende Referenzdichten, die
gemäß
abhängende Referenzdichten, die
gemäß

mit den Ladungszahlen  zusammenhängen.
Da die Teilchendichten ui der diffundierenden Spezies nun
nicht mehr zu
zusammenhängen.
Da die Teilchendichten ui der diffundierenden Spezies nun
nicht mehr zu
 gehören (sie liegen lediglich im dualen Raum),
werden die Gleichungen in den chemischen Aktivitäten bi=ui/pi0
formuliert,
die weiterhin H1-Größen sein sollen.
Die Modellgleichungen enthalten m
Kontinuitätsgleichungen
gekoppelt mit einer nichtlinearen Poissongleichung
und sehen wie folgt aus:
gehören (sie liegen lediglich im dualen Raum),
werden die Gleichungen in den chemischen Aktivitäten bi=ui/pi0
formuliert,
die weiterhin H1-Größen sein sollen.
Die Modellgleichungen enthalten m
Kontinuitätsgleichungen
gekoppelt mit einer nichtlinearen Poissongleichung
und sehen wie folgt aus:
|  |
(1) |
Dabei ist 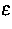 die Dielektrizität, f eine fixierte Ladungsdichte,
und
die Dielektrizität, f eine fixierte Ladungsdichte,
und  ist die Ladungsdichte
der Elektronen und Löcher.
Für die ersten l Spezies (Punktdefekte und Dotand-Defekt-Paare) nehmen wir
diffusiven und konvektiven Transport an, der durch den Stromausdruck
ist die Ladungsdichte
der Elektronen und Löcher.
Für die ersten l Spezies (Punktdefekte und Dotand-Defekt-Paare) nehmen wir
diffusiven und konvektiven Transport an, der durch den Stromausdruck
![\begin{displaymath}
j_i=-D_i(\cdot,b,\psi)p_{i0}\big[\nabla b_i+Q_i(\psi)\,
b_i\nabla\psi\big],~
i=1,\dots,l,\end{displaymath}](../1999/img57.gif)
gegeben ist. Ein Beispiel für
die  -Abhängigkeit der betrachteten
Diffusionskoeffizienten Di sowie der Ladungen Qi
ist für verschiedene Prozesstemperaturen in Abb. 1 dargestellt.
In allen Kontinuitätsgleichungen treten Volumenquellterme auf, die durch
Reaktionen
der Form
-Abhängigkeit der betrachteten
Diffusionskoeffizienten Di sowie der Ladungen Qi
ist für verschiedene Prozesstemperaturen in Abb. 1 dargestellt.
In allen Kontinuitätsgleichungen treten Volumenquellterme auf, die durch
Reaktionen
der Form

Abb. 1:
Phosphor-Interstitial-Paare in Silizium:
Diffusionskoeffizient (links) und Ladungszahl (rechts) als Funktion des
chemischen Potentials  bei verschiedenen Temperaturen (nach
[1]).
bei verschiedenen Temperaturen (nach
[1]).
 |
entstehen, wobei
 die Vektoren der stöchiometrischen Koeffizienten bezeichnen.
Die entsprechenden Reaktionsraten
die Vektoren der stöchiometrischen Koeffizienten bezeichnen.
Die entsprechenden Reaktionsraten  lauten
gemäß dem Massenwirkungsgesetz
lauten
gemäß dem Massenwirkungsgesetz

Gemeint sind damit verschiedene Paarbildungs- und
Generations-Rekombinationsreaktionen.
Für alle nicht diffundierenden Spezies Xi (Dotanden) wird die Existenz
einer Reaktion der Form
| ![\begin{displaymath}
R_{\alpha\beta}^\Omega=k^\Omega_{\alpha \beta}
\big[\prod_{j=1}^l a_j^{\alpha_j}-a_i^2\big]\end{displaymath}](../1999/img63.gif) |
(2) |
vorausgesetzt (Generation-Rekombination verschiedener Dotand-Defekt-Paare).
Zwischen den diffundierenden Spezies Xi,  , können
zusätzlich Randreaktionen mit Reaktionsraten
, können
zusätzlich Randreaktionen mit Reaktionsraten
![\begin{displaymath}
R_{\alpha\beta}^\Gamma(x,b_1,\dots,b_l,\psi)=
k^\Gamma_{\alp...
...1}^l a_i^{\beta_i}\Big],~
x\in\Gamma,~ b\in\IR^l_+,~\psi\in\IR,\end{displaymath}](../1999/img65.gif)
auftreten.
Die kinetischen Koeffizienten
Di,  und
und  hängen außer von
hängen außer von  noch vom Ort und
vom Zustand selbst (beschrieben durch den Vektor
noch vom Ort und
vom Zustand selbst (beschrieben durch den Vektor  ) ab.
) ab.
Die in [3] benutzten Methoden zu
energetischen Abschätzungen
können für den betrachteten Fall von Heterostrukturen adaptiert werden, was
auf die folgenden Resultate führt: Das Problem (1) besitzt einen durch
 eindeutig bestimmten stationären Zustand
eindeutig bestimmten stationären Zustand  . Die
freie Energie
. Die
freie Energie
![\begin{displaymath}
F(u)=\int\Big\{\frac{\varepsilon}{2}\vert\nabla\psi\vert^2+g...
...[\ln{\frac{u_i}{p_{i0}}}-1\big]+p_{i0}\big\}\Big\}
\,\mbox{d}x,\end{displaymath}](../1999/img71.gif)
wobei  und
und
 die eindeutig bestimmte Lösung der Poissongleichung zu u ist,
ist entlang von Lösungen von (1) beschränkt und fällt monoton und
exponentiell gegen ihren Gleichgewichtswert F(u*). Diese energetischen
Abschätzungen bilden die Grundlage für weitere
a priori-Abschätzungen
für Lösungen von (1).
die eindeutig bestimmte Lösung der Poissongleichung zu u ist,
ist entlang von Lösungen von (1) beschränkt und fällt monoton und
exponentiell gegen ihren Gleichgewichtswert F(u*). Diese energetischen
Abschätzungen bilden die Grundlage für weitere
a priori-Abschätzungen
für Lösungen von (1).
Unter der für Paardiffusionsmodelle erfüllten Voraussetzung, dass die
Quellterme
aus den Volumenreaktionen maximal zweiter Ordnung sind, haben wir im räumlich
zweidimensionalen Fall
die Existenz globaler oberer Schranken für die Teilchendichten ui
nachgewiesen.
Dazu werden zunächst die  - und
- und
 -Normen der chemischen Aktivitäten bi
abgeschätzt.
Hier verwenden wir die Voraussetzung (2) und Folgerungen aus dem
exponentiellen
Fallen der freien Energie entlang von Lösungen von (1), um die aus der
Drift und den Reaktionen resultierenden Terme zu kontrollieren.
Eine anschließende Moser-Iteration liefert für die
diffundierenden Spezies
globale obere Schranken für die chemischen Aktivitäten bi und
Teilchendichten ui, mit deren Kenntnis schließlich auch die
entsprechenden Schranken für die nicht diffundierenden Spezies gewonnen
werden.
-Normen der chemischen Aktivitäten bi
abgeschätzt.
Hier verwenden wir die Voraussetzung (2) und Folgerungen aus dem
exponentiellen
Fallen der freien Energie entlang von Lösungen von (1), um die aus der
Drift und den Reaktionen resultierenden Terme zu kontrollieren.
Eine anschließende Moser-Iteration liefert für die
diffundierenden Spezies
globale obere Schranken für die chemischen Aktivitäten bi und
Teilchendichten ui, mit deren Kenntnis schließlich auch die
entsprechenden Schranken für die nicht diffundierenden Spezies gewonnen
werden.
Für strikt positive Anfangswerte haben wir globale positive
untere Schranken für die chemischen Aktivitäten bi und
Teilchendichten ui hergeleitet. Von der Länge des
Zeitintervalls abhängende Abschätzungen
 sichern zunächst die Zulässigkeit von Testfunktionen der Form
sichern zunächst die Zulässigkeit von Testfunktionen der Form

Die erste Testfunktion
führt für  auf
auf
 , mittels der zweiten
Testfunktion und Moser-Iteration gelangen wir zu positiven globalen unteren
Schranken für die chemischen Aktivitäten bi,
, mittels der zweiten
Testfunktion und Moser-Iteration gelangen wir zu positiven globalen unteren
Schranken für die chemischen Aktivitäten bi,  .Hieraus können aufgrund der vorhandenen Reaktion (2)
die entsprechenden Resultate für die nicht diffundierenden Spezies
gewonnen werden.
.Hieraus können aufgrund der vorhandenen Reaktion (2)
die entsprechenden Resultate für die nicht diffundierenden Spezies
gewonnen werden.
Mit Hilfe der a priori-Abschätzungen und des exponentiellen Fallens der
freien Energie haben wir weitere Aussagen zum
asymptotischen Verhalten
von Lösungen des Paardiffusionsmodells (1)
erhalten. Insbesondere nähern sich die Teilchendichten ui,
die chemischen Aktivitäten bi und das chemische Potential der Elektronen
 in jeder Lp-Norm exponentiell ihrem Gleichgewichtswert. Aufgrund von
Regularitätsaussagen für elliptische Gleichungen gilt die Asymptotik
für
in jeder Lp-Norm exponentiell ihrem Gleichgewichtswert. Aufgrund von
Regularitätsaussagen für elliptische Gleichungen gilt die Asymptotik
für  auch in der
auch in der  -Norm. Für die ausführliche Diskussion
der hier vorgestellten Paardiffusionsmodelle
verweisen wir auf [2].
-Norm. Für die ausführliche Diskussion
der hier vorgestellten Paardiffusionsmodelle
verweisen wir auf [2].
Aussagen zur Lösbarkeit von (1) sind Gegenstand aktueller Untersuchungen,
Resultate für den Fall einer homogenen glatt berandeten Struktur
sind in [4] zu finden.
Projektliteratur:
- K. GHADERI, G. HOBLER,
Simulation of phosphorus diffusion in silicon
using a pair diffusion model with a reduced number of parameters, J.
Electrochem. Soc., 142 (1995), pp. 1654-1658.
- A. GLITZKY, R. HÜNLICH,
Global properties of pair diffusion models, in Vorbereitung.
- R. HÜNLICH, A. GLITZKY, On energy estimates for
electro-diffusion
equations arising in semiconductor technology, in: Partial differential
equations. Theory and numerical solution (W. Jäger, J. Necas,
O. John, K. Najzar, J. Stará, Hrsg.), Research Notes
in Mathematics, 406, Chapman & Hall/CRC, Boca Raton,
2000, pp. 158-174.
- W. MERZ, A. GLITZKY, R. HÜNLICH, K. PULVERER,
Strong solutions for
pair diffusion models in homogeneous semiconductors,
Preprint SFB-438-9921, SFB 438, TU München, Univ. Augsburg, 1999.
LaTeX typesetting by I. Bremer
1/16/2001
![]() das
chemische Potential der Elektronen,
das
chemische Potential der Elektronen, ![]() sind geeignet gewählte
vom Ort und von
sind geeignet gewählte
vom Ort und von ![]() abhängende Referenzdichten, die
gemäß
abhängende Referenzdichten, die
gemäß


![]()
![]()

![]() die Vektoren der stöchiometrischen Koeffizienten bezeichnen.
Die entsprechenden Reaktionsraten
die Vektoren der stöchiometrischen Koeffizienten bezeichnen.
Die entsprechenden Reaktionsraten ![]() lauten
gemäß dem Massenwirkungsgesetz
lauten
gemäß dem Massenwirkungsgesetz

![\begin{displaymath}
R_{\alpha\beta}^\Omega=k^\Omega_{\alpha \beta}
\big[\prod_{j=1}^l a_j^{\alpha_j}-a_i^2\big]\end{displaymath}](../1999/img63.gif)
![\begin{displaymath}
R_{\alpha\beta}^\Gamma(x,b_1,\dots,b_l,\psi)=
k^\Gamma_{\alp...
...1}^l a_i^{\beta_i}\Big],~
x\in\Gamma,~ b\in\IR^l_+,~\psi\in\IR,\end{displaymath}](../1999/img65.gif)
![]() eindeutig bestimmten stationären Zustand
eindeutig bestimmten stationären Zustand ![]() . Die
freie Energie
. Die
freie Energie
![\begin{displaymath}
F(u)=\int\Big\{\frac{\varepsilon}{2}\vert\nabla\psi\vert^2+g...
...[\ln{\frac{u_i}{p_{i0}}}-1\big]+p_{i0}\big\}\Big\}
\,\mbox{d}x,\end{displaymath}](../1999/img71.gif)
![]() - und
- und
![]() -Normen der chemischen Aktivitäten bi
abgeschätzt.
Hier verwenden wir die Voraussetzung (2) und Folgerungen aus dem
exponentiellen
Fallen der freien Energie entlang von Lösungen von (1), um die aus der
Drift und den Reaktionen resultierenden Terme zu kontrollieren.
Eine anschließende Moser-Iteration liefert für die
diffundierenden Spezies
globale obere Schranken für die chemischen Aktivitäten bi und
Teilchendichten ui, mit deren Kenntnis schließlich auch die
entsprechenden Schranken für die nicht diffundierenden Spezies gewonnen
werden.
-Normen der chemischen Aktivitäten bi
abgeschätzt.
Hier verwenden wir die Voraussetzung (2) und Folgerungen aus dem
exponentiellen
Fallen der freien Energie entlang von Lösungen von (1), um die aus der
Drift und den Reaktionen resultierenden Terme zu kontrollieren.
Eine anschließende Moser-Iteration liefert für die
diffundierenden Spezies
globale obere Schranken für die chemischen Aktivitäten bi und
Teilchendichten ui, mit deren Kenntnis schließlich auch die
entsprechenden Schranken für die nicht diffundierenden Spezies gewonnen
werden.
![]() sichern zunächst die Zulässigkeit von Testfunktionen der Form
sichern zunächst die Zulässigkeit von Testfunktionen der Form

![]() in jeder Lp-Norm exponentiell ihrem Gleichgewichtswert. Aufgrund von
Regularitätsaussagen für elliptische Gleichungen gilt die Asymptotik
für
in jeder Lp-Norm exponentiell ihrem Gleichgewichtswert. Aufgrund von
Regularitätsaussagen für elliptische Gleichungen gilt die Asymptotik
für ![]() auch in der
auch in der ![]() -Norm. Für die ausführliche Diskussion
der hier vorgestellten Paardiffusionsmodelle
verweisen wir auf [2].
-Norm. Für die ausführliche Diskussion
der hier vorgestellten Paardiffusionsmodelle
verweisen wir auf [2].