Mikromechanik und Molekulare Dynamik

[Next]:

Martensitische Umwandlung

[Up]:

Projektbeschreibungen

[Previous]:

Anfangs- und Randwertprobleme für hyperbolische Systeme

[Contents]

[Index]

Mikromechanik und Molekulare Dynamik

Bearbeiter: W. Dreyer , M. Kunik

Kooperation: W. H. Müller (Heriot-Watt-Universität Edinburgh), T. Hauck (Motorola München)

Beschreibung der Forschungsarbeit:Die Molekulare Dynamik geht aus von der Formulierung der Dynamik von Mikroteilchen und leitet durch Mittelwertbildung die makroskopischen Gesetze des aus diesen Mikroteilchen zusammengesetzten Körpers ab. Unter Mikroteilchen verstehen wir die kleinsten Einheiten, die zum Verständnis gewisser makroskopischer Phänomene betrachtet werden müssen. Viele Fragestellungen in unseren laufenden Projekten erfordern mikromechanische Betrachtungen. Hierzu gehören beispielsweise:

In Phasenfeldtheorien ist die Kopplung zwischen Diffusion und den hierdurch erzeugten Spannungen auf der makroskopischen Ebene ein nicht gänzlich verstandenes Phänomen. Zur Klärung leiten wir die freie Energie molekulardynamisch ab.
Die makroskopische Modellierung von Phasengrenzflächen erfordert in deren Umgebung ein mikromechanisches Studium des Spannungs/Dehnungs-Zusammenhanges.
Anfangs- und Randwertprobleme für hochgradig nichtlineare hyperbolische Systeme lassen sich durch einfache Integrationen lösen, falls es gelingt, die betrachteten Systeme mittels kinetischer Gleichungen herzuleiten. Makroskopische hyperbolische Systeme lassen sich aber auch molekulardynamisch generieren, weshalb wir versuchen, die kinetische Dreyer/Kunik-Methode auch molekulardynamisch zu etablieren.

Zur Illustration betrachten wir einen eindimensionalen Festkörper, der aus einer Kette von Atomen aufgebaut ist. Die Atome mit Orten 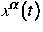$x^{\alpha }(t)$ und Geschwindigkeiten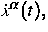 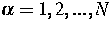$\dot{x}^{\alpha }(t),$ $\alpha =1,2,...,N$ , genügen den Newtonschen Bewegungsgleichungen

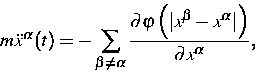$\begin{displaymath} m\ddot{x}^{\alpha }(t)=-\sum\limits_{\beta \neq \alpha} \fra... ...ert x^{\beta }-x^{\alpha }\vert\right) }{\partial x^{\alpha }},\end{displaymath}$ (28)

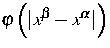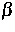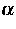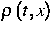wo m die Masse eines Atoms ist, und $\varphi \left( \vert x^{\beta }-x^{\alpha }\vert\right)$ das Potential bezeichnet, welches zwischen den Atomen $\beta$ und $\alpha$ besteht. Aus den Newtonschen Gleichungen lassen sich unter gewissen Annahmen Feldgleichungen für die Makrovariablen $\rho \left( t,x\right)$ - Massendichte und 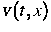$\mbox{\sl v} \left( t,x\right)$ - Geschwindigkeit ableiten, nämlich

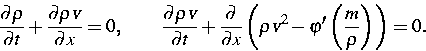$\begin{displaymath} \frac{\partial \rho }{\partial t}+\frac{\partial \rho \mbox{... ...{2}-\varphi ^{\prime }\left( \frac{m}{\rho }\right) \right) =0.\end{displaymath}$ (29)

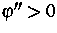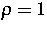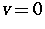Dies ist ein hyperbolisches System, falls $\varphi ^{\prime \prime }\gt$ gilt. Die Güte der gemachten Annahmen, die zu (2) führen, läßt sich nun dadurch testen, daß wir ein Anfangswertproblem sowohl mit (1) als auch mit (2) lösen. Wir betrachten ein Riemannsches Anfangswertproblem mit $\rho =1$ und $\mbox{\sl v}=0$ für x<0 und für 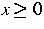$x\geq 0$ wählen wir 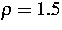$\rho =1.5$ und berechnen 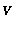$\mbox{\sl v}$ aus der (2) zugeordneten Rankine-Hugoniot-Beziehung, so daß ein einzelner Stoß entsteht.

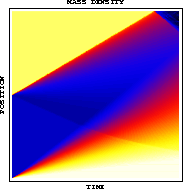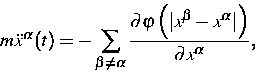
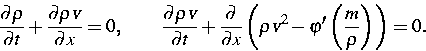
$\parbox{0.4\textwidth}{\begin{figure} \ProjektEPSbildNocap {\textwidth}{stoss.eps} \end{figure}}$ Die nebenstehende Abbildung zeigt das Dichtefeld, so wie es aus den Newtonschen Gleichungen für N=10000 Atome folgt. Würden nun die gemachten Annahmen, die im wesentlichen die thermischen Schwankungen vernachlässigen, für dieses Anfangswertproblem angemessen sein, dann müßte nach (2) das gleiche Bild herauskommen. Das tut es nicht, denn das System (2) liefert einen Einzelstoß, der in die obere rechte Ecke einmündet. Dies Beispiel zeigt somit eindrucksvoll, wie die Güte phänomenologischer Annahmen mittels Molekulardynamik beurteilt werden kann. Inzwischen wurde das System (2) durch Berücksichtigung der Temperatur verallgemeinert. Ein WIAS-Preprint hierzu ist in Vorbereitung.