Bearbeiter: W. Dreyer
,
M. Kunik
Beschreibung der Forschungsarbeit:Dies ist eine Fortführung und Erweiterung der
Untersuchung über Anwendungen des
Maximum-Entropie-Prinzips, [1], [2]. Das aktuelle Ziel des Projektes
ist die Entwicklung einer Theorie für Anfangs- und Randwertprobleme
für solche hyperbolischen Systeme, die auf einer darunterliegenden
mikroskopischen Theorie basieren. Im Berichtszeitraum untersuchten wir
hyperbolische
Wärmeleitungsprozesse in Kristallen bei
Temperaturen von etwa 10 K. Die mikroskopische Theorie ist
hier die kinetische Theorie von Phononen, und das hyperbolische System
besteht aus Feldgleichungen für die Variablen
K. Die mikroskopische Theorie ist
hier die kinetische Theorie von Phononen, und das hyperbolische System
besteht aus Feldgleichungen für die Variablen 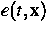 -
Energiedichte und
-
Energiedichte und 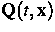 - Wärmefluß. Diese lauten
bei Beschränkung auf eine makroskopische Raumdimension in schwacher
Formulierung
- Wärmefluß. Diese lauten
bei Beschränkung auf eine makroskopische Raumdimension in schwacher
Formulierung
| 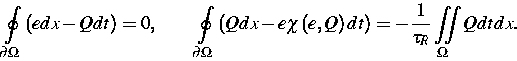 |
(18) |
Die nichtlineare Funktion 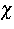 von e und Q ist gegeben durch
von e und Q ist gegeben durch
| 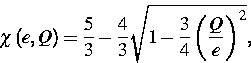 |
(19) |
und 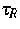 ist eine konstante Relaxationszeit. Schließlich gibt es
eine Entropieungleichung, nämlich
ist eine konstante Relaxationszeit. Schließlich gibt es
eine Entropieungleichung, nämlich
| 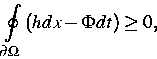 |
(20) |
mit expliziten Funktionen 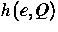 für die Entropiedichte
und
für die Entropiedichte
und 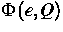 für den Entropiefluß, die [3] entnommen
werden können.
für den Entropiefluß, die [3] entnommen
werden können.
Wir betrachten das Anfangs- und Randwertproblem für ein halbunendliches
Gebiet und geben vor:
| 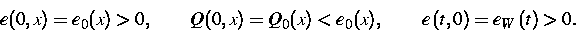 |
(21) |
Es ist uns gelungen, die kinetische Lösung
dieses Problems anzugeben. Hierzu benötigen wir einige Abkürzungen
und Definitionen, die in [3] ausführlich interpretiert werden und hier
nur dazu dienen, die formale Struktur der Lösung aufzuzeigen.
Die Funktion
| 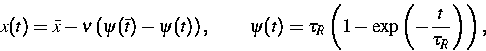 |
(22) |
definiert Mikrocharakteristiken. Die Größe
| 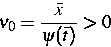 |
(23) |
trennt Anfangsdaten von Randdaten. Die Schnittpunkte einer
Mikrocharakteristik durch den Punkt 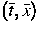 mit der
Anfangsachse t=0, bzw. mit dem Rand x=0, sind gegeben durch
mit der
Anfangsachse t=0, bzw. mit dem Rand x=0, sind gegeben durch
| ![\begin{displaymath}
x_{0}(\bar{t},\bar{x},\nu )=\bar{x}-\psi (\bar{t})\nu ,\qqua...
...{t}}{\tau _{R}}\right) +\frac{\bar{x}}{\tau _{R}\nu }\right] ~.\end{displaymath}](../../1998/html/images/img344.gif) |
(24) |
Die zu integrierende zentrale Funktion lautet
| 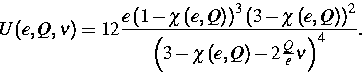 |
(25) |
Es folgt der Darstellungssatz für die kinetische Lösung des Anfangs-
und Randwertproblems an irgendeiner Stelle 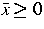 auf einem
Zeitstreifen
auf einem
Zeitstreifen 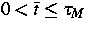 , wobei
, wobei 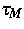 ein positiver
Zeitschritt ist.
ein positiver
Zeitschritt ist.
![\begin{eqnarray}
e(\bar{t},\bar{x}) &=&\int\limits_{-1}^{\nu _{0}}U(e_{0}(x_{0}(...
...(t_{W}(\bar{t},\bar{x},\nu )),\nu )\,\nu \,d\nu ~\right]
~. \notag\end{eqnarray}](../../1998/html/images/img349.gif)
Der Darstellungssatz enthält noch eine unbekannte Funktion 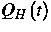 , welche Lösung einer algebraischen Gleichung ist. Mit den
Abkürzungen
, welche Lösung einer algebraischen Gleichung ist. Mit den
Abkürzungen
| 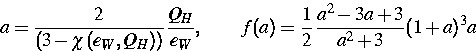 |
(26) |
lautet diese algebraische Gleichung
| 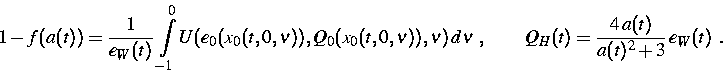 |
(27) |
Der mathematische Inhalt von (12) ist eine Stetigkeitsbedingung, die
garantiert, daß die Lösung bei Annäherung an den Rand die
Randdaten auch annimmt.
Die Darstellungsformeln (9) und (10) gestatten die iterative
Berechnung der Felder e,Q, die zunächst noch vom Zeitschritt 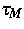 abhängen, aber für
abhängen, aber für 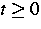 und
und 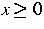 Bilanzgleichungen
sowie eine Entropieungleichung der Form (1) und (3) exakt
erfüllen. Erst im Grenzfall
Bilanzgleichungen
sowie eine Entropieungleichung der Form (1) und (3) exakt
erfüllen. Erst im Grenzfall 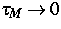 erhalten wir die
exakte Lösung des lokalen hyperbolischen Systems (1), (2) und (3).
erhalten wir die
exakte Lösung des lokalen hyperbolischen Systems (1), (2) und (3).
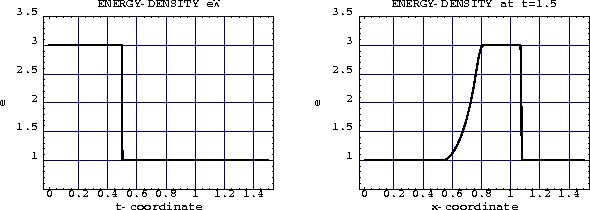
Beispielhaft betrachten wir die Anfangsbedingung e(0,x)=1,Q(0,x)=0 sowie
die Randbedingung 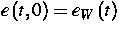 mit
mit 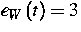 für 0<t<0.5 und
für 0<t<0.5 und 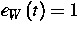 für
für 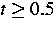 . Die hieraus entstehende Struktur wurde hier für den
Grenzfall
. Die hieraus entstehende Struktur wurde hier für den
Grenzfall 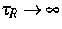 berechnet.
berechnet.
Projektliteratur:
- W. DREYER, M. KUNIK, The maximum
entropy principle revisited, Contin. Mech. Thermodyn., 10 (1998),
No. 6, pp. 331-347.
-
 , Reflections of
Eulerian shock waves at moving adiabatic boundaries, Monte Carlo
Methods and Appl., 4 (1998), No. 3, pp. 231-252.
, Reflections of
Eulerian shock waves at moving adiabatic boundaries, Monte Carlo
Methods and Appl., 4 (1998), No. 3, pp. 231-252.
-
 , Initial and boundary value
problems of hyperbolic heat conduction, WIAS-Preprint No. 438,
1998, erscheint in: Contin. Mech. Thermodyn. (1999).
, Initial and boundary value
problems of hyperbolic heat conduction, WIAS-Preprint No. 438,
1998, erscheint in: Contin. Mech. Thermodyn. (1999).
LaTeX typesetting by I. Bremer
7/30/1999
![]() K. Die mikroskopische Theorie ist
hier die kinetische Theorie von Phononen, und das hyperbolische System
besteht aus Feldgleichungen für die Variablen
K. Die mikroskopische Theorie ist
hier die kinetische Theorie von Phononen, und das hyperbolische System
besteht aus Feldgleichungen für die Variablen ![]() -
Energiedichte und
-
Energiedichte und ![]() - Wärmefluß. Diese lauten
bei Beschränkung auf eine makroskopische Raumdimension in schwacher
Formulierung
- Wärmefluß. Diese lauten
bei Beschränkung auf eine makroskopische Raumdimension in schwacher
Formulierung
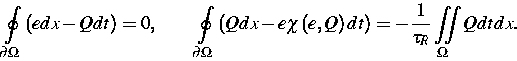
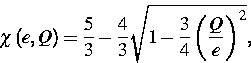
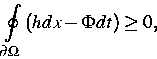
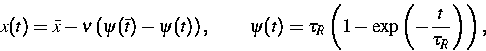
![\begin{displaymath}
x_{0}(\bar{t},\bar{x},\nu )=\bar{x}-\psi (\bar{t})\nu ,\qqua...
...{t}}{\tau _{R}}\right) +\frac{\bar{x}}{\tau _{R}\nu }\right] ~.\end{displaymath}](../../1998/html/images/img344.gif)
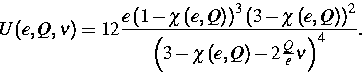
![]() , welche Lösung einer algebraischen Gleichung ist. Mit den
Abkürzungen
, welche Lösung einer algebraischen Gleichung ist. Mit den
Abkürzungen
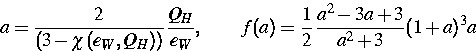
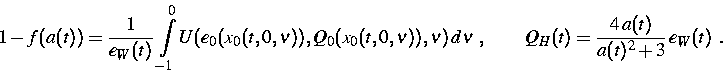
![]() abhängen, aber für
abhängen, aber für ![]() und
und ![]() Bilanzgleichungen
sowie eine Entropieungleichung der Form (1) und (3) exakt
erfüllen. Erst im Grenzfall
Bilanzgleichungen
sowie eine Entropieungleichung der Form (1) und (3) exakt
erfüllen. Erst im Grenzfall ![]() erhalten wir die
exakte Lösung des lokalen hyperbolischen Systems (1), (2) und (3).
erhalten wir die
exakte Lösung des lokalen hyperbolischen Systems (1), (2) und (3).
![]() mit
mit ![]() für 0<t<0.5 und
für 0<t<0.5 und ![]() für
für ![]() . Die hieraus entstehende Struktur wurde hier für den
Grenzfall
. Die hieraus entstehende Struktur wurde hier für den
Grenzfall ![]() berechnet.
berechnet.