[Next]:

Waveletalgorithmen für die Randelementmethode

[Up]:

Projektbeschreibungen

[Previous]:

Optimierungsprobleme mit zufälligen und nichtglatten Daten

 [Contents] 

 [Index] 

Subsections

• 1. Effektive numerische Verfahren zur Lösung von Integralgleichungen erster Art
• 2. Zur Gewinnung von Aussagen über die Bodendurchlässigkeit aus unvollständig gegebenen Meßdaten
• 3. Zur Bestimmung von Punktquellen in der Wellengleichung: Einzigkeit, Stabilität und numerische Verfahren

Inverse Probleme der Hydrodynamik und Seismik

Bearbeiter: G. Bruckner , S. Prößdorf  

Kooperation: H.-J. Diersch (WASY GmbH), S. V. Pereverzev (Ukrainische Akademie der Wissenschaften, Kiew), M. Yamamoto (Universität Tokio)

Beschreibung der Forschungsarbeit:

1. Effektive numerische Verfahren zur Lösung von Integralgleichungen erster Art

 

Die Integralgleichung mit logarithmischem Kern,

$$-\frac{1}{\pi}\int_{\partial\Omega}\ln\vert x-y\vert\phi(y)ds(y)= f(x),\quad x\in \partial\Omega,$$

die auch Symmsche Integralgleichung  genannt wird, ist die äquivalente potentialtheoretische Formulierung des Dirichlet-Problems für die Laplace-Gleichung in dem ebenen Gebiet $\Omega.$ Damit besitzt sie ein breites Anwendungsspektrum auf stationäre, homogene Probleme der Hydrodynamik, Elektrodynamik und Elastizitätstheorie.

In konkreten Anwendungen unterliegen die Daten f Meßfehlern, und auch die Randkurve $\partial\Omega$ ist mitunter nur näherungsweise gegeben. Diesen Umstand hat man wegen der Schlechtgestelltheit der Symmschen Integralgleichung bei ihrer numerischen Lösung zu berücksichtigen.

In [4] werden für die Symmsche Integralgleichung vollständig diskretisierte Regularisierungsverfahren  begründet, die ökonomisch in Bezug auf den Rechenaufwand und von optimaler Konvergenzordnung sind. Die Stabilisierung erfolgt dabei durch geeignete Wahl des Diskretisierungsparameters. Verfahren dieser Art sind auch auf andere Integralgleichungen erster Art anwendbar.

2. Zur Gewinnung von Aussagen über die Bodendurchlässigkeit aus unvollständig gegebenen Meßdaten

 

Ausgangspunkt der Untersuchungen ist die Arbeit [1], die aus dem Projekt ,,Bestimmung der Bodendurchlässigkeit aus Wasserständen``  des Jahres 1996 entstanden ist. In [1] wurde die direkte Inversionsmethode von Vainikko für die stationäre zweidimensionale Diffusionsgleichung kombiniert mit einer die a-priori-Information einbeziehenden Methode der Datenglättung. Erforderlich war eine solche Kombination, da die gegebenen Meßdaten im allgemeinen nicht auf allen Knoten der Diskretisierung gegeben sind, wie es die Methode von Vainikko verlangt hätte. In [1] kommentierte Beispielrechnungen ergaben erstens, daß man durchaus auch mit weniger Meßdaten brauchbare Ergebnisse erhalten kann, und zweitens, daß es für lokale Aussagen genügt, wenn lokal ausreichend viele Meßdaten gegeben sind.

Für den Anwender sind Aussagen über die Bodendurchlässigkeit aus Messungen des Wasserstandes (Potentialmessungen) von großem Interesse, da solche Messungen meist ohnehin vorhanden oder mit relativ geringem Aufwand zu beschaffen sind.

Optimal wäre die Beantwortung der folgenden Frage: Gegeben seien ein Block von geologischen Informationen und ein Satz von Meßdaten. Welche zusätzlichen Messungen müssen mindestens durchgeführt werden, um (global oder lokal) die Bodendurchlässigkeit bestimmen zu können? Da der Anwender an Aufwandsminimierung interessiert sein muß, liegt hier die Betonung auf dem Wort ,,mindestens``.

Als Teilaspekte dieser komplexen Aufgabenstellung sind auch negative Feststellungen von Interesse, etwa von der Art: Gibt es in einem Teilgebiet keine Messungen, so kann für dieses Teilgebiet nichts ausgesagt werden.

Der rigorose Beweis dieser anschaulich recht plausiblen Feststellung führt mathematisch auf die Frage der Sensibilität  des direkten Problems. Das (finite-Elemente-)diskretisierte direkte Problem lautet

$$L{\bf u}={\bf d},$$

wo ${\bf u}$ der Vektor der Potentialwerte in den Knotenpunkten, ${\bf d}$ die aus Quellen und Senken im Gebiet sowie Zu- und Abflüssen durch den Rand gebildeten rechten Seiten und L eine schwach besetzte Matrix sind. In L gehen die auf jedem finiten Element als konstant vorausgesetzten Durchlässigkeiten ein.

Fixiert man eines der finiten Elemente F₀ und betrachtet die Ableitung nach der F₀ zugeordneten Durchlässigkeit, so ergibt sich

$${\bf u}'=L^{-1}L'L^{-1}{\bf d}.$$

Aufgrund der ,,lokalen`` Bauart der Matrix L' erhält man für den beliebigen Knoten X

$$u_X'=\sum_P\Lambda_{XP}a_P,$$

wobei die Summation über die Knoten P von F₀ läuft, a_P von Null verschieden ist und nur von F₀ abhängt und $\Lambda_{XP}$ die Einträge in die Matrix L^-1 sind.

Bewegt sich X von F₀ weg, so kann aus einem Abklingverhalten von $\Lambda_{XP}$, $P\in F_0$ fixiert, folglich auf ein Abklingen von u_X' geschlossen werden.

Ein solches Abklingverhalten bei Inversen von Fast-Diagonal-Matrizen wurde in Arbeiten zur Wavelet-Analyse von anderen Autoren theoretisch fundiert (vgl. [5]). Auf die Matrix L läßt sich diese Theorie jedoch nicht unmittelbar anwenden. Das erfordert eine noch ausstehende geeignete Modifizierung, die es möglich macht, das Abklingen auch quantitativ genau zu untersuchen.

Das Abklingverhalten wird durch Rechenbeispiele veranschaulicht.

3. Zur Bestimmung von Punktquellen in der Wellengleichung: Einzigkeit, Stabilität und numerische Verfahren

 

Hier untersuchen wir das inverse Problem der Rekonstruktion von Punktquellen 

$$\{N,\alpha_1,\cdots,\alpha_N,x_1,\cdots,x_N\}$$

in der Wellengleichung 

$$\begin{eqnarray*} \frac{\partial^2u}{\partial t^2}(x,t)&=&\frac{\partial^2u}{\pa... ...)&=&0,\;\;u'(x,0)=0,\;\;\;0<x<1,\ u(0,t)&=&u(1,t)=0,\;\;\;0<t<T,\end{eqnarray*}$$

aus der Beobachtung von $u(\eta,t)$ in einem fixierten Punkt $\eta\in (0,1)$. Dabei sind $\lambda\in C^1[0,T],\;\lambda(0)\ne 0, \;\alpha_k\in \IR$ und $x_k\in (0,1)$.

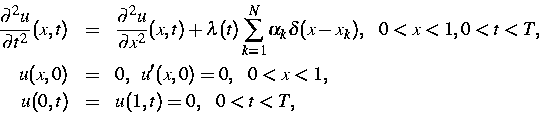
Im Falle, daß die Funktion $\lambda$ exakt gegeben ist, werden in [2] Einzigkeit für irrationales $\eta$ und eine Stabilitätsabschätzung in der H¹(0,T)-Norm der Beobachtung bewiesen. Die Stabilitätsabschätzung kann dabei nur unter zusätzlichen Bedingungen an die Unbekannten $\{x_1,\cdots,x_N\}$ gezeigt werden. Außerdem leiten wir numerische Verfahren ab, die stabil sind gegenüber L²(0,T)-Beobachtungsfehlern.

Der Fall, daß die Funktion $\lambda$ nicht exakt, sondern nur näherungsweise gegeben ist, wird in Hinsicht auf stabile numerische Verfahren in [3] betrachtet. Dazu zerlegen wir das Problem in einen gutgestellten und einen schlechtgestellten Anteil und formulieren den schlechtgestellten Anteil als Integralgleichung erster Art mit gestörtem Kern . Das der Behandlung einer solchen Integralgleichung zugrundeliegende Konzept ist auf eine ganze Klasse von Operatorgleichungen anwendbar.

Projektliteratur:

1.  G. BRUCKNER, S. HANDROCK-MEYER, H. LANGMACH, An inverse problem from 2d ground-water modelling, Inverse Problems, 14 (1998), pp. 835-851.
2.  G. BRUCKNER, M. YAMAMOTO, Determination of point wave sources by pointwise observations: Stability and reconstruction, WIAS-Preprint Nr. 441, 1998.
3.  , On an operator equation with noise in the operator and the right-hand side with application to an inverse vibration problem, WIAS-Preprint Nr. 407, 1998.
4.  S. V. PEREVERZEV, S. PrÖssdorf$\dagger$, On the characterization of self-regularization properties of a fully discrete projection method for Symm's integral equation, WIAS-Preprint Nr. 394, 1998.
5.  P. TCHAMITCHIAN, Wavelets, functions and operators, in: Wavelets: Theory and applications, (G. Erlebacher, M. Y. Hussaini, L. Jameson, Hrsg.), ICASE/LaRC Series in Computational Science and Engineering, Oxford University Press, 1996, pp. 83-181.

[Next]:

Waveletalgorithmen für die Randelementmethode

[Up]:

Projektbeschreibungen

[Previous]:

Optimierungsprobleme mit zufälligen und nichtglatten Daten

 [Contents] 

 [Index]