 |
|
|
|
[Contents] | [Index] |
Bearbeiter: R. Henrion , A. Möller
Kooperation: W. Römisch (Humboldt-Universität (HU) zu Berlin), G. Wozny (Technische Universität (TU) Berlin), T. Szántai (Technische Universität Budapest)
Förderung: DFG-Schwerpunktprogramm ,,Echtzeitoptimierung großer Systeme``
Beschreibung der Forschungsarbeit:
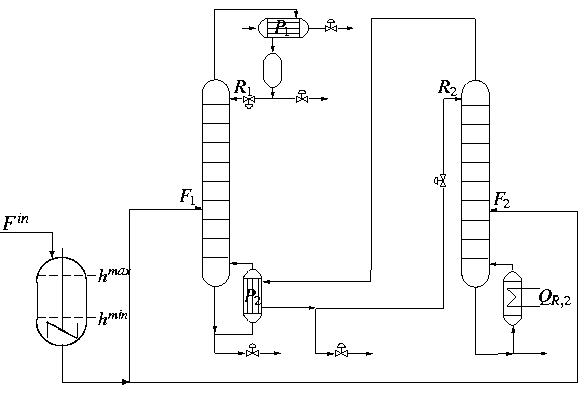
1. Schwerpunkt der Arbeit ist die Fortführung des gemeinsam mit Prof. G. Wozny (TU Berlin) und Prof. W. Römisch (HU Berlin) geleiteten DFG-Projekts Optimierung integrierter Kolonnensysteme unter stochastischen Echtzeitbedingungen . Gegenstand des Projekts ist die Ermittlung einer energieminimalen Fahrweise von Destillationskolonnen im kontinuierlichen Betrieb, die robust gegenüber wechselnden stochastischen Einflüssen auf den Prozeß ist. Die Abbildung zeigt das Schema einer Pilotanlage an der TU Berlin (energetisch gekoppelte Hoch- und Niederdruckkolonne). Der Zufluß Fin (in der Praxis aus vorgelagerten industriellen Prozessen) stellt den wesentlichen stochastischen Parameter mit den beiden Komponenten Fließgeschwindigkeit und Zusammensetzung dar, in dessen Unkenntnis die für einen bestimmten Planungshorizont optimale Steuerung der Anlage vorauszuberechnen ist.
Als Konsequenz werden folgende Restriktionen des entstehenden Optimierungsmodells stochastisch: die Produktspezifikationen (Mindestreinheiten, in denen die Bestandteile des zu trennenden Gemisches am Kolonnenkopf bzw. im Sumpf vorliegen), die Feed-Tank-Restriktionen (Verhinderung des Voll- oder Leerlaufens des Tanks, siehe Abb.) sowie Zyklusrestriktionen (Vermeidung einer Optimierung zulasten nachfolgender Planungszeiträume). Um zu behandelbaren Nebenbedingungen zu gelangen, wird im Sinne der angestrebten Robustheit der Fahrweise verlangt, daß die Restriktionen entsprechend der Zufallsverteilung des stochastischen Parameters mit einer vorgegebenen Mindestwahrscheinlichkeit einzuhalten sind (Wahrscheinlichkeitsrestriktionen) .
2. Im Mittelpunkt der Arbeit im Berichtszeitraum stand die Formulierung eines geeigneten konkreten Optimierungsmodells [1] sowie die numerische Behandlung von Wahrscheinlichkeitsrestriktionen . Letztere Frage wurde intensiv während des einmonatigen Gastaufenthaltes von Prof. T. Szántai in Berlin untersucht. Insbesondere wurden auf der Basis effektiver Methoden zur Berechnung von Werten von Verteilungsfunktionen (z. B. [7]) Varianten zur Einbeziehung zweiter Ableitungen der Restriktionsfunktionen analysiert. Hierdurch soll es gelingen, die Bearbeitung von Wahrscheinlichkeitsrestriktionen aus dem bisher üblichen Rahmen von Verfahren erster Ordnung in den Kontext von SQP-Verfahren zu überführen. Eine konkrete Kopplung mit dem Programmsystem SNOPT [2] wird Gegenstand der weiteren Arbeit sein.
Die Benutzung von (stichproben-basierten) Schätzungen des zugrundeliegenden Wahrscheinlichkeitsmaßes bei der praktischen Umsetzung des oben skizzierten Problems wirft die Frage nach der Stabilität von Lösungen und Optimalwerten in Optimierungsproblemen mit Wahrscheinlichkeitsrestriktionen bei kleinen Störungen des Maßes auf. Hierzu wurden in [3] verifizierbare Bedingungen an das Originalproblem bei Betrachtung allgemeinster Daten hergeleitet (insbesondere sind auch Nichtglattheiten sowohl bei den Restriktionsfunktionen als auch bezüglich des Wahrscheinlichkeitsmaßes berücksichtigt). Für die praktisch relevante Klasse konvexer Probleme mit Wahrscheinlichkeitsrestriktionen , die durch r-konkave Maße induziert werden, konnten entsprechend konkretere Bedingungen sowohl für qualitative [4] als auch für quantitative Stabilität [5] gefunden werden. Die erhaltenen Resultate werfen eine Reihe weiterer Fragen von theoretischem Interesse auf, z. B. unter welchen Bedingungen an die Dichten r- konkave Maße strenge Konvexitätseigenschaften besitzen, oder welche geometrische Struktur Wahrscheinlichkeitsrestriktionen aufweist. Nichtglattheiten von Eingangsdaten sind neben den betrachteten stochastischen Optimierungsproblemen (etwa in Gestalt der Verteilungsfunktion zu empirischen Maßen oder Maßen mit kompaktem Träger) auch in anderen Gebieten wie der semi-infiniten Optimierung typisch. Untersuchungen hierzu wurden im Zusammenhang mit der Charakterisierung der metrischen Regularität von Ungleichungssystemen in [6] vorgenommen.
Projektliteratur:
|
|
|
[Contents] | [Index] |