[Next]:

Optimierungsprobleme mit zufälligen und nichtglatten Daten

[Up]:

Projektbeschreibungen

[Previous]:

Projektbeschreibungen

 [Contents] 

 [Index] 

Subsections

• 1. Behandlung der konischen Diffraktion
• 2. Weitere analytische Untersuchungen des optimalen Design-Problems
• 3. Erweiterung des Programmsystems DIPOG zur Lösung direkter und inverser Diffraktionsprobleme bei binären und Multilevel-Gittern

Direkte und inverse Probleme für diffraktive Strukturen in der Optik

Bearbeiter: J. Elschner , R. Hinder , G. Schmidt  

Kooperation: H.-J. Rostalski (Raytek GmbH Berlin), B. Kleemann (Carl Zeiss Oberkochen), F. Wyrowski (Universität Jena), J. Bischoff (Carl Zeiss Jena)

Förderung: BMBF

Beschreibung der Forschungsarbeit:

Ziel des Projekts ist die analytische und numerische Behandlung direkter und inverser Beugungsprobleme an binären optischen Gittern  auf Dünnschichtsystemen. Solche mikrooptischen Elemente realisieren optische Eigenschaften und Funktionen, die mit traditionellen optischen Elementen nicht erreichbar sind (Laserkollimation und Modenformung, Strahlteilung, Polarisationsschalter).

1. Behandlung der konischen Diffraktion

   

 

Abb. 1: Konische Diffraktion am periodischen Beugungsgitter

Das Beugungsgitter wird durch eine periodische, stückweise konstante Funktion $\epsilon$ charakterisiert, die sich aus den Dielektrizitätskonstanten der unterschiedlichen Materialien zusammensetzt. Eine einfallende ebene Welle wird durch das Gitter gebeugt, wobei endlich viele ausfallende Wellen reflektiert bzw. transmittiert werden. Die Modellierung erfolgt mittels der zeitharmonischen Maxwellschen Gleichungen mit den bekannten Stetigkeitsbedingungen an den Materialgrenzen und Ausstrahlungsbedingungen im Unendlichen.

In [4] wird die Äquivalenz des Transmissionsproblems für die Maxwellschen Gleichungen im ${\IR}^3$zu einem System von zwei Variationsgleichungen im $\IR^2$ gezeigt. Die Analysis des Variationsproblems liefert eine vollständige Lösbarkeitstheorie für das Problem der konischen Diffraktion sowie Aussagen zur analytischen Abhängigkeit der Lösung von Frequenz und Einfallswinkeln. Außerdem werden die Singularitäten des elektromagnetischen Feldes an den Kanten genau bestimmt. Die starke Elliptizität der entsprechenden Bilinearform für alle physikalisch relevanten Gittermaterialien sichert die Konvergenz von Finite-Element-Verfahren zur Wirkungsgradberechnung von periodischen Gittern bei konischem Einfall ebener Wellen.

2. Weitere analytische Untersuchungen des optimalen Design-Problems

   

Die Kenntnis der Gradienten der Rayleigh-Koeffizienten bezüglich Änderungen des Gitterprofils ist die Grundlage effektiver Optimierungsverfahren zur Bestimmung einer optimalen Gittergeometrie ([1, 3]). In Zusammenarbeit mit S. Nazarov (St. Petersburg) wurde ein neuer Zugang entwickelt, der die Berechnung dieser Größen durch Kurvenintegrale ermöglicht. Dadurch konnten erstmalig effektive Formeln im Falle beliebiger Lösungssingularitäten und mehrerer zusammenstoßender Materialien abgeleitet werden. Dieser Zugang erlaubt auch die Behandlung des optimalen Design-Problems für die konische Diffraktion.

3. Erweiterung des Programmsystems DIPOG zur Lösung direkter und inverser Diffraktionsprobleme bei binären und Multilevel-Gittern

   

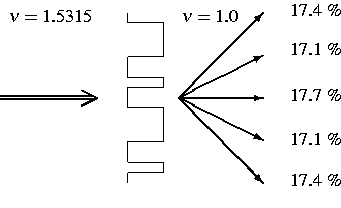
Die auf Gradientenverfahren beruhenden Algorithmen zum optimalen Entwurf von Beugungsgittern bei der klassischen Diffraktion wurden in Zusammenarbeit mit R. Henrion verfeinert, um zusätzliche Restriktionen besser innerhalb des Optimierungsproblems behandeln zu können. Nunmehr kann für Gitter mit vorgegebenen Materialien und bestimmten technologischen Vorgaben die optimale Gittergeometrie durch einen Optimierungszyklus bestimmt werden. Es wurde eine Vielzahl von Zielfunktionen implementiert, so daß die Gitter nach unterschiedlichen Kriterien an das Fernfeld optimiert werden können ([3, 5]). Abbildung 2 zeigt das Ergebnis der Berechnung eines einfachen Strahlteilers, der senkrecht einstrahlendes Licht in fünf gleich starke Strahlen mit vorgegebener Aufspreizung spalten soll.

 

Abb. 2: Optimales Profil eines 1-zu-5 Strahlteilers. Wellenlänge $\lambda =0.633\mu$m, Periode $d=1.79 \mu$m, Gitterhöhe $H=0.77 \mu$m, Verteilung der Gitterpunkte: 0., 0.12, 0.36, 0.76

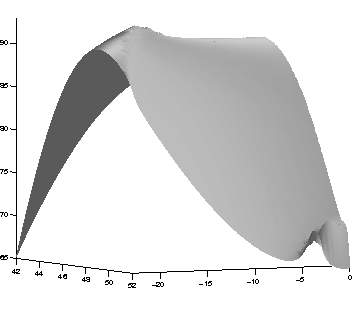
Es wurde ein Code zur Lösung des direkten Problems der konischen Diffraktion implementiert, der eine wichtige Ergänzung des Programmsystems DIPOG darstellt. Grundlage ist eine verallgemeinerte Finite-Element-Diskretisierung des Systems von Variationsgleichungen. Durch den modularen Aufbau von DIPOG konnte auf existierende Routinen zur effektiven Behandlung der nichtlokalen Randoperatoren, zur Minimierung des bei der FE-Lösung auftretenden Defekts zwischen exakter und numerischer Wellenzahl sowie zur effektiven Lösung der nichtsymmetrischen Gleichungssysteme zurückgegriffen werden. Erste Berechnungen für einfache binäre Gitter bei schrägem Einfall des Lichts wurden durchgeführt, wobei teilweise eine starke Abhängigkeit der Effizienz einzelner Moden vom Einfallswinkel auftritt. An der Implementierung von Verfahren zur Behandlung des optimalen Design-Problems bei der konischen Diffraktion wird gegenwärtig gearbeitet.

 

Abb. 3: Effizienz der -2. Ordnung eines Transmissionsgitters in Abhängigkeit von den Einfallswinkeln einer ebenen Welle mit dem Wellenvektor $(\sin{\theta} \cos{\phi}, - \cos{\theta} \cos{\phi}, \sin{\phi})$, $\theta=42^\circ...52^\circ,\phi=-23^\circ...0^\circ$

Projektliteratur:

1.  G. BAO, D. DOBSON, Modeling and optimal design of diffractive optical structures, erscheint in: Surveys Math. Indust.
2.  J. ELSCHNER, G. SCHMIDT, Diffraction in periodic structures and optimal design of binary gratings. Part I: Direct problems and gradient formulas, Math. Methods Appl. Sci., 21 (1998), pp. 1297-1342.
3.  , Numerical solution of optimal design problems for binary gratings, J. Comput. Phys., 146 (1998), pp. 603-626.
4.  J. ELSCHNER, R. HINDER, F. PENZEL, G. SCHMIDT, Existence, uniqueness and regularity for solutions of the conical diffraction problem, WIAS-Preprint Nr. 400, 1998, erscheint in: Math. Models Methods Appl. Sci.
5.  H.-J. ROSTALSKI, J. GUHR, B. KLEEMANN, J. ELSCHNER, G. SCHMIDT, M. FERSTL, E. PAWLOWSKI, R. STEINGRÜBER, G. BOSTANJOGLO, R. MOTZKUS, Use of a multilayer dielectric diffraction grating as the resonator mirror of a neodymium-doped yttrium aluminium garnet laser, J. Modern Opt., 45 (1998), pp. 1523-1535.

[Next]:

Optimierungsprobleme mit zufälligen und nichtglatten Daten

[Up]:

Projektbeschreibungen

[Previous]:

Projektbeschreibungen

 [Contents] 

 [Index]