![\makeatletter
\@ZweiProjektbilderNocap[h]{0.48\textwidth}{komp49-org.ps}{komp49.ps}
\makeatother](../../1998/html/images/img187.gif) |
|
|
|
[Contents] | [Index] |
Kooperation: B. Hegner (BASF AG, Ludwigshafen)
Beschreibung der Forschungsarbeit: Die Arbeiten aus dem Vorjahr wurden entsprechend dem Kooperationsvertrag bzw. Arbeitsplan mit den Schwerpunkten
 Eine besonders wichtige Fragestellung war in diesem Zusammenhang die
Berechnung von Parametern, für die alle Nebenbedingungen des jeweiligen
Problems erfüllt sind. Nebenbedingungen gelten als erfüllt, wenn die
zugeordneten Funktionen nicht-negative Werte annehmen.
Im eingesetzten SQP-Verfahren wird dazu eine
Straffunktion, die mit Hilfe der Nebenbedingungen definiert wird,
minimiert.
Bei Nebenbedingungen mit negativen lokalen
Maxima in Abhängigkeit der Parameter führt dieses Vorgehen nicht immer
zum Ziel.
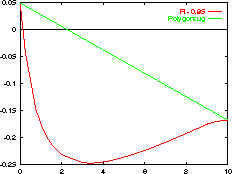
In der nebenstehenden Abbildung hat eine der geforderten Reinheiten
ein negatives lokales Maximum in Abhängigkeit von der
Schaltzeit. Bei diesem Beispiel wurde
neben dem Einsatz einer stochastischen Methode die zusätzliche
Einführung eines Homotopieparameters mit Erfolg getestet.
Dabei wird zu der Funktion, die die Werte für die jeweilige
Nebenbedingung liefert, eine modifizierte Form durch Verbindung der
lokalen Maxima berechnet und beide Funktionen in Linearkombination,
gewichtet über den Homotopiefaktor, für die Berechnung der
Nebenbedingung verwendet.
Im obigen Beispiel kann man durch den Homotopieparameter erreichen, daß die Suche
gültiger Parameter am
Anfang nicht nach rechts, sondern nach links startet.
Eine besonders wichtige Fragestellung war in diesem Zusammenhang die
Berechnung von Parametern, für die alle Nebenbedingungen des jeweiligen
Problems erfüllt sind. Nebenbedingungen gelten als erfüllt, wenn die
zugeordneten Funktionen nicht-negative Werte annehmen.
Im eingesetzten SQP-Verfahren wird dazu eine
Straffunktion, die mit Hilfe der Nebenbedingungen definiert wird,
minimiert.
Bei Nebenbedingungen mit negativen lokalen
Maxima in Abhängigkeit der Parameter führt dieses Vorgehen nicht immer
zum Ziel.
In der nebenstehenden Abbildung hat eine der geforderten Reinheiten
ein negatives lokales Maximum in Abhängigkeit von der
Schaltzeit. Bei diesem Beispiel wurde
neben dem Einsatz einer stochastischen Methode die zusätzliche
Einführung eines Homotopieparameters mit Erfolg getestet.
Dabei wird zu der Funktion, die die Werte für die jeweilige
Nebenbedingung liefert, eine modifizierte Form durch Verbindung der
lokalen Maxima berechnet und beide Funktionen in Linearkombination,
gewichtet über den Homotopiefaktor, für die Berechnung der
Nebenbedingung verwendet.
Im obigen Beispiel kann man durch den Homotopieparameter erreichen, daß die Suche
gültiger Parameter am
Anfang nicht nach rechts, sondern nach links startet.
Ein weiterer wichtiger Punkt war die Frage der korrekten Behandlung unzulässiger Parameterbereiche, die implizit durch die Gültigkeitsbereiche der benutzten Modelle gegeben sind. Der verwendete SQP-Algorithmus wurde entsprechend ergänzt.
Durch die adaptive Schrittweitensteuerung in der der Optimierung zugrundeliegenden Simulation der Destillationskolonnen erhält man zu benachbarten Parametern u. U. eine andere Diskretisierung. Dadurch wird im allgemeinen der SQP-Algorithmus nicht konvergieren. Dieses Problem konnte dadurch gelöst werden, daß einige Iterationen vor dem Erreichen der maximal erlaubten Anzahl der Iterationen des SQP-Algorithmus das Schrittweitenraster ,,eingefroren`` wird und nur noch eine Verfeinerung erlaubt ist.
Das SQP-Verfahren setzt eine (mehr oder weniger) glatte Abhängigkeit der Funktionale von den zu variierenden Parametern voraus. Das Diskretisierungsverfahren im vorliegenden Simulator ist relativ ungenau, wie die durchgeführte Studie zu einer mathematisch fundierten adaptiven Schrittweitensteuerung zeigt (Abb. 1). Das führt immer wieder zu Problemen im Konvergenzverhalten des SQP-Verfahrens, da die geforderte Glattheit nicht genügend gewährleistet werden kann. Eine weitere Vertiefung der Optimierungsproblematik setzt deshalb die Umstellung des Diskretisierungsansatzes und damit eine wesentliche Änderung des Programmpakets beim Industriepartner voraus.
Die Arbeiten an dem Projekt wurden mit der Übergabe der Software im Sommer 1998 formal abgeschlossen.
Projektliteratur:
|
|
|
[Contents] | [Index] |