Stabilitätswechsel in Mehrskalensystemen

[Next]:

Forschungsgruppe Numerische Mathematik und Wissenschaftliches Rechnen

[Up]:

Projektbeschreibungen

[Previous]:

Optimale Steuerung diskontinuierlicher Destillationsprozesse

[Contents]

[Index]

Stabilitätswechsel in Mehrskalensystemen

Bearbeiter: K. R. Schneider

Kooperation: V. F. Butuzov, N. N. Nefedov (Staatliche Universität Moskau)

Förderung: DFG: Kooperationsprojekt ,,Singulär gestörte Systeme und Stabilitätswechsel`` deutscher und russischer Wissenschaftler im Rahmen des Memorandum of Understanding zwischen DFG und RFFI

Beschreibung der Forschungsarbeit:

Die Dynamik schneller bimolekularer Reaktionen kann unter Verwendung von singulär gestörten Differentialgleichungen beschrieben werden. Wir betrachten das Randwertproblem

$\begin{eqnarray} \varepsilon^2 u'' & = & g(u,v,x,\varepsilon), \ v''= f(u,v,x,\varepsilon), \ u'(0) = u'(1) =0, \ v(0) = v^0, \ v(1) =v^1,\end{eqnarray}$

das als stationäres Problem des zugehörigen Reaktions-Diffusions-Systems aufgefaßt werden kann, und das Anfangs-Randwertproblem

$\begin{eqnarray} \varepsilon^2 u'' & = & g(u,v,x,\varepsilon), \ v'= f(u,v,x,\varepsilon), \ u'(0) = u'(1) =0, \ v(0) = v^0\end{eqnarray}$

unter der Voraussetzung, daß das assoziierte System

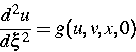
$\begin{displaymath} \frac{d^2 u}{d\xi^2} = g(u,v,x,0)\end{displaymath}$

zwei Familien von Gleichgewichtslösungen besitzt, die sich schneiden (Stabilitätswechsel). In diesem Fall kann die Standardtheorie für Differentialgleichungen vom Tichonovschen Typ zur Lösung der gestellten Probleme nicht angewendet werden. Um hinreichende Bedingungen für die Lösbarkeit der gestellten Probleme ableiten zu können, führen wir den Begriff der singulären stabilen Lösung für das ausgeartete Problem $(\varepsilon = 0)$ ein. Die entsprechenden Funktionen werden unter Verwendung von Glättungsverfahren zur Konstruktion von geordneten Ober- und Unterlösungen verwendet. Mit deren Hilfe kann auf die Existenz einer Lösung bei beiden Aufgabenstellungen geschlossen und deren asymptotisches Verhalten bezüglich $\varepsilon$ bestimmt werden. Die erhaltenen Resultate können zur Untersuchung des Verhaltens von Reaktionsraten verwendet werden.

Projektliteratur:

V. F. BUTUZOV, N. N. NEFEDOV, K. R. SCHNEIDER, Singularly perturbed boundary value problems for systems of Tichonov's type in case of exchange of stabilities, WIAS-Preprint No. 408 , 1998, erscheint in: J. Differential Equations.