[Next]:

Optimale Steuerung diskontinuierlicher Destillationsprozesse

[Up]:

Projektbeschreibungen

[Previous]:

Langzeitverhalten skalarer Reaktions-Diffusions-Gleichungen

 [Contents] 

 [Index] 

Subsections

• Teilprojekt: Homokline Bifurkationen in Hamiltonschen Systemen
• Teilprojekt: Homokline Bifurkationen von vierdimensionalen symplektischen Abbildungen

Homokline Bifurkationen

 

Bearbeiter: D. Turaev  

Förderung: DFG-Schwerpunktprogramm ,,Ergodentheorie, Analysis und effiziente Simulation dynamischer Systeme``

Beschreibung der Forschungsarbeit:

Teilprojekt: Homokline Bifurkationen in Hamiltonschen Systemen

   

Es wurde die Struktur von N-homoklinen Orbits   zu einem (im Koordinatenursprung gelegenen) Sattelpunkt in Hamiltonschen Systemen der Gestalt

$$\begin{eqnarray*} \frac{dx}{dt} & = & - A^{T} (\mu) x + \dots , \ \frac{dy}{d... ...da_n (\mu)\}, \ 0 < \mbox{Re } \lambda_i (\mu), \ i=1,2,\dots ,n\end{eqnarray*}$$

betrachtet, wobei N beliebig groß sein kann. Es ist bekannt, daß die Existenz einer einfachen homoklinen Schleife zu einem Gleichgewichtspunkt vom Sattel-Fokus-Typ im allgemeinen die Existenz von unendlich vielen N-homoklinen Orbits impliziert, wobei N beliebig groß sein kann. Im Gegensatz dazu können im Falle eines Sattelpunktes (die führenden Eigenwerte von A, d. h. die Eigenwerte mit dem kleinsten Realteil, sind reell) keine N-homoklinen Orbits in allgemeiner Lage auftreten, d. h. ein 1-homokliner Orbit stellt keinen Grenzwert einer Folge von N-homoklinen Orbits dar. In Anwendungen konnten aber N-Pulse mit einem monotonen asymptotischen Verhalten nachgewiesen werden. Um diesen ,,Widerspruch`` aufzuklären und um eine umfassende Beschreibung möglicher Szenarien für das Auftreten von N-homoklinen Orbits zu geben, wurden die Kodimension 1-Bifurkationen von homoklinen Orbits zu einem hyperbolischen Fixpunkt studiert. Es wurden zwei Kodimension 1-Bifurkationen von homoklinen Orbits zu einem Sattelpunkt eines Hamiltonschen Systems entdeckt, die zum Auftreten von N-homoklinen Orbits führen. Die erste Bifurkation ist eine Orbit-Flip-Bifurkation, die zweite entspricht der Bifurkation eines führenden zweifachen Eigenwertpaares, die aber halbeinfach sind, in Gegenwart einer zusätzlichen Symmetrie. In beiden Fällen konnte eine vollständige Beschreibung der Struktur der N-homoklinen Orbits gegeben werden, die während der Bifurkation entsteht.

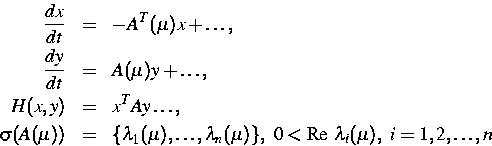
Im Falle der Orbit-Flip-Bifurkationen wurde die Möglichkeit des Auftretens von sogenannten superhomoklinen Orbits (diese sind homoklin zu einem homoklinen Orbit, siehe Abbildung 1) bewiesen. Wir zeigen, daß die Existenz eines superhomoklinen Orbits die Menge der N-homoklinen Orbits bereichert und geben eine Beschreibung dieser Menge in der Sprache der Knoten-Invarianten.

 

Abb. 1:  Superhomokliner Orbit zu einer homoklinen Schleife

Projektliteratur:

1.  D. TURAEV, On codimension 1-bifurcations of homoclinic orbits in Hamiltonian systems, in Vorbereitung.

Teilprojekt: Homokline Bifurkationen von vierdimensionalen symplektischen Abbildungen

     

Kooperation: L. Shilnikov, S. Gonchenko (Universität Nizhny Novgorod)

Symplektische Abbildungen treten beim Studium der Poincaré-Abbildung von Hamiltonschen Systemen auf. Die Dynamik zweidimensionaler symplektischer Abbildungen (sie können bei Hamiltonschen Systemen mit zwei oder $1 \frac{1}{2}$-Freiheitsgraden beobachtet werden) wird mehr oder weniger gut verstanden, nicht zuletzt auch wegen zahlreicher umfangreicher numerischer Simulationen. Die Phasenraumstruktur solcher Abbildungen kann als ,,chaotische See`` mit elliptischen Inseln bildhaft charakterisiert werden. Wir bezeichnen diese Struktur als ,,gemischte`` Struktur. Im Gegensatz dazu kann die Phasenraumstruktur höherdimensionaler symplektischer Abbildungen nicht einmal bildhaft beschrieben werden. Das Ziel des Forschungsprojektes bestand darin, einen Mechanismus für das Auftreten stabiler periodischer Lösungen   in vierdimensionalen symplektischen Abbildungen mit chaotischer Dynamik aufzufinden, der als Indikator dafür angesehen werden kann, daß die Phasenraumstruktur auch im höherdimensionalen Fall als ,,gemischt`` angesehen werden kann. Die Untersuchungen bezogen sich auf die Bifurkation einer vierdimensionalen symplektischen Abbildung mit einer homoklinen Tangierung   zu einer sattelartigen periodischen Lösung. Es wurde bewiesen, daß bei einer solchen Bifurkation keine periodischen Orbits entstehen, falls die Multiplikatoren der sattelartigen periodischen Lösung reell sind. Im Gegensatz dazu entstehen stabile periodische Lösungen im Falle komplexer Multiplikatoren.

Projektliteratur:

1.  S. GONCHENKO, D. TURAEV, L. SHILNIKOV, Elliptic periodic orbits near a homoclinic tangency in four-dimensional symplectic diffeomorphisms, erscheint in: J. Regular and Chaotic Dynamics.

[Next]:

Optimale Steuerung diskontinuierlicher Destillationsprozesse

[Up]:

Projektbeschreibungen

[Previous]:

Langzeitverhalten skalarer Reaktions-Diffusions-Gleichungen

 [Contents] 

 [Index]