Hysteresephänomene in der Elastoplastizität

[Next]:

Adaptive Optimierung von Flugprofilen mit Gedächtnislegierungen

[Up]:

Projektbeschreibungen

[Previous]:

Phasenfeldsysteme

[Contents]

[Index]

Hysteresephänomene in der Elastoplastizität

Bearbeiter: P. Krejcí , M. Siegfanz , J. Sprekels

Kooperation: M. Brokate (Christian-Albrechts-Universität zu Kiel), D. Rachinskii (Institut für Probleme der Informationsübertragung, Moskau)

Beschreibung der Forschungsarbeit:

Dynamische Modelle der Elastoplastizität, die in der Praxis am häufigsten Verwendung finden, beziehen sich direkt oder indirekt auf die Variationsungleichung

$\begin{displaymath} \left\{ \begin{array} {l} \big< \dot u(t) - \dot x(t), x(t) ... ...] x(t) \in Z \, , \quad x(0) = x^0 \in Z \, ,\end{array}\right.\end{displaymath}$ (4)

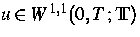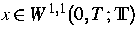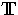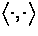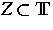wobei $u\in W^{1,1}(0,T\,;\IT)$ (,,Input``) und $x\in W^{1,1}(0,T\,;\IT)$ (,,Output``) innere Variablen sind, z. B. Dehnung und plastische Spannung, $\IT$ ein Vektorraum mit Skalarprodukt $\big<\cdot, \cdot\big\gt$ , $t\in [0,T]$ die Zeit und $Z\subset \IT$ eine konvexe abgeschlossene Teilmenge von 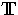$\IT$ ist. Der Punkt bezeichne die Ableitung nach t.

Diese Aufgabe stellt den grundlegenden Baustein der mathematischen Plastizitätstheorie dar. Der Lösungsoperator

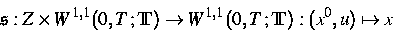
$\begin{displaymath} {\frak s}: Z \times W^{1,1}(0,T\,;\IT) \to W^{1,1}(0,T\,;\IT) : (x^0, u) \mapsto x\end{displaymath}$

heißt Stop mit Charakteristik Z; seine Eigenschaften werden seit den siebziger Jahren systematisch untersucht.

a) Die Arbeit [9] wurde als Zusammenfassung bisheriger Resultate für die Sommerschule ,,Seminar in Differential Equations``, Chvalatice/Tschechische Republik, Juni 1998 vorbereitet. Darin werden die analytischen Eigenschaften des Stop-Operators in den Funktionenräumen 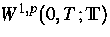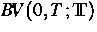$W^{1,p}(0,T\,;\IT)$ , $BV(0,T\,;\IT)$ und $C([0,T];\IT)$ hinsichtlich der Geometrie der konvexen Menge Z vorgestellt. 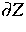Neue Ergebnisse wurden für den Spezialfall eines glatten Randes $\partial Z$ erzielt. Es wurde bewiesen, daß der Stop-Operator lokal Lipschitz-stetig ist. Eine optimale Abschätzung für die Lipschitz-Konstante wurde hergeleitet.

b) Die Theorie der Stop-Operatoren wurde für die Untersuchung eines Gleichungssystems der eindimensionalen Thermovisko-Elastoplastizität verwendet

$\begin{eqnarray} &&u_{tt} - \gamma u_{xx} - \left({\cal P} [u_x, \theta]\right)... ... P} [u_x, \theta] u_{xt} + \mu u^2_{xt} - \beta \theta u_{xt}\, ,\end{eqnarray}$

mit geeigneten Anfangs- und Randbedingungen. Die plastische Spannung ${\cal P} [u_x, \theta]$ wird als der temperaturabhängige Prandtl-Ishlinskii-Operator

$\begin{displaymath} {\cal P} [u_x, \theta] := \int^\infty_0 \varphi (r,\theta)\, {{\frak s}}_r [u_x]\, d r\end{displaymath}$ (5)

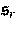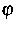in Form einer unendlichen Kombination von eindimensionalen Stop-Operatoren ${{\frak s}}_r$ mit Charakteristiken [-r,r], r>0, und mit einer gegebenen temperaturabhängigen Dichtefunktion $\varphi$ dargestellt. Der Hysterese-Operator

$\begin{displaymath} {\cal V} [u_x, \theta] := \frac{1}{2} \int^\infty_0 (\varph... ... \theta \varphi_\theta (r, \theta))\, {\frak s}^2_r [u_x]\, dr\end{displaymath}$ (6)

entspricht dem thermoplastischen Anteil der inneren Energie. Mit Hilfe des Prandtl-Ishlinskii-Operators können vielfältige Hysteresephänomene, wie z. B. innere Schleifen, modelliert werden.

Die Existenz und Eindeutigkeit der globalen Lösung wurde schon früher in [3] bewiesen. In [7] wurde jetzt das asymptotische Verhalten für 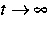$t \to \infty$ untersucht.

c) Um Probleme wie (2), (3) numerisch zu lösen, wurde ein Approximationsschema für Prandtl-Ishlinskii-Operatoren entwickelt. Zur numerischen Lösung wurden Spezialfälle der Gleichungen (2), (3) mit Hilfe eines Differenzenverfahrens diskretisiert. Für den temperaturunabhängigen Fall wurde die numerische Approximation implementiert und getestet. Die Untersuchungen zur Konvergenz des numerischen Verfahrens und Fehlerabschätzungen sind noch in Arbeit.

Projektliteratur:

M. BROKATE, P. KREJCí, Wellposedness of kinematic hardening models in elastoplasticity, Math. Model. Num. Anal. (M²AN), 32 (1998), pp. 177-209.
P. KREJCí , J. SPREKELS, Global solutions to a coupled parabolic-hyperbolic system with hysteresis in 1-d magnetoelasticity, Nonlin. Anal., 33 (1998), pp. 341-358.
$\dito$ , Temperature-dependent hysteresis in one-dimensional thermovisco-elastoplasticity, Appl. Math., 43 (1998), pp. 173-205.
$\dito$ , Hysteresis operators in phase-field models of Penrose-Fife type, Appl. Math., 43 (1998), pp. 207-222.
M. BROKATE, P. KREJCí, D. RACHINSKII, Some analytical properties of the multidimensional continuous Mróz model of plasticity, Control Cybernet., 27 (1998), pp. 199-215.
M. BROKATE, P. KREJCí, On the wellposedness of the Chaboche model, in $\,:\,$ Control and Estimation of Distributed Parameter Systems (W. Desch, F. Kappel, K. Kunisch, Hrsg.), Proceedings of the conference held in Vorau (Austria), July 14-20, 1996, Int. Series Num. Math., Vol. 126, Birkhäuser, Basel, 1998, pp. 67-79.
P. KREJCí, J. SPREKELS, Weak stabilization of solutions to PDEs with hysteresis in thermovisco-elastoplasticity, in: Proceedings of Equadiff 9, Conference on Differential Equations and Their Applications, Brno, August 25-29, 1997 (R. P. Agarwal, F. Neuman, J. Vosmanský, Hrsg.), Masaryk University, Brno & Electronic Publishing House, Stony Brook, NY, 1998, pp. 81-96.
$\dito$ , Hysteresis operators in phase-field models, in: Topics in Nonlinear Analysis - The Herbert Amann Anniversary Volume (J. Escher, G. Simonett, Hrsg.), Birkhäuser Verlag, Basel, 1999, pp. 499-515.
P. KREJCí, Evolution variational inequalities and multidimensional hysteresis operators, WIAS-Preprint No. 432, 1998.

Abb. 1:

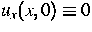Numerische Lösung der Bewegungsgleichung $u_{tt} - \left({\cal P} [u_x]\right)_x = 0\,$ , mit Neumannschen Randbedingungen, u_t(x,0)=13(1-x), $u_x(x,0)\equiv 0$ , T=4.0, ${\cal P}$ wie in Abb. 2.

links: Numerisch berechnete S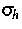pannung $\sigma_h$ als Funktion von Ort und Zeit.