Phasenfeldsysteme

[Next]:

Hysteresephänomene in der Elastoplastizität

[Up]:

Projektbeschreibungen

[Previous]:

Modellierung und Simulation von hochsperrenden Bauelementen

[Contents]

[Index]

Phasenfeldsysteme

Bearbeiter: O. Klein , P. Krejcí , J. Sprekels

Kooperation: P. Colli (Universität Pavia), M. Frémond (LMSGC, Paris)

Förderung: ESF/FBP Research Fellowship, VIGONI

Beschreibung der Forschungsarbeit: Diffusive Phasenübergänge, wie z. B. das Kristallwachstum, werden häufig durch Phasenfeldsysteme modelliert. In derartigen Systemen ist eine Evolutionsgleichung für die absolute Temperatur $\theta$ , die sich aus einer Energiebilanz ergibt, mit einer Evolutionsgleichung für den sogenannten Ordnungsparameter $\chi$ des Phasenübergangs gekoppelt.

Im Rahmen des Projektes wurden im Berichtszeitraum verschiedene Phasenfeldsysteme untersucht.

a) In Fortführung der Arbeiten der Vorjahre wurden in [6] zeitliche Semidiskretisierungen für Phasenfeldsysteme vom Penrose-Fife-Typ , vgl. [12],
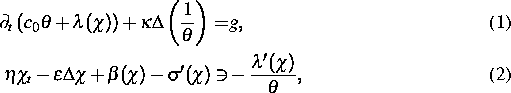
$\begin{align} \partial_t\left(c_0 \theta + \lambda(\chi)\right) + \kappa \Delta... ...+ \beta(\chi) - \sigma'(\chi) \ni& - \frac{\lambda'(\chi)}{\theta},\end{align}$
untersucht. Hierbei sind c₀, $\kappa$ und $\varepsilon$ positive Konstanten, g ist eine von Ort und Zeit abhängige Funktion, $\eta$ ist eine vom Ort abhängige positive Funktion und $\beta$ ist ein maximal monotoner Graph.

Es gelang dabei, in Verbesserung der Resultate aus [4, 5], Konvergenzaussagen auch für den Fall herzuleiten, daß die Nichtlinearitäten $\lambda$ , $\sigma$ nur noch stetig differenzierbar mit lokal Lipschitz-stetiger Ableitung sind, was den Anwendungsbereich der Theorie erheblich erweitert. Mit Hilfe von Ansätzen aus [11] gelang ferner der Nachweis, daß, für eine Zeitschrittweite h, der Diskretisierungsfehler O(h) ist, während in [4, 5] nur $O(\sqrt{h})$ gezeigt wurde.

b) Zur Modellierung des Erstarrens von unterkühltem Wasser wurde von Frémond in [2] das folgende modifizierte Stefan-Problem eingeführt:
$\begin{align} c_0\partial_t{\theta} - \kappa \Delta \theta = g \quad & \text{im... ...a)}{\theta_M} \quad \quad & \text{auf der Grenzschicht Wasser/Eis.}\end{align}$
Hierbei sind $\left[ \cdot \right]$ der Sprung einer Größe entlang der Grenzschicht zwischen Wasser und Eis, W_N die Normalengeschwindigkeit der Grenzschicht, L eine positive Konstante und $c(\theta)$ eine Funktion der Temperatur.

Um dieses Problem näherungsweise zu lösen, wurde das folgende Phasenfeldsystem betrachtet:
$\begin{align} \partial_t\left(c_0 \theta + L \chi\right) - \kappa \Delta \theta... ...{[0,1]}(\chi) \ni & \frac{L}{\theta_M}\left(\theta - \theta_M\right).\end{align}$
Hierbei ist $\phi(\nabla \beta, \theta)$ eine geeignete Näherung von $\frac{c(\theta)}{\left\vert\nabla \chi\right\vert}$ .Es gelang in [1], die Lösbarkeit dieses Systems nachzuweisen.

c) Phasenübergänge werden häufig von Hysterese-Phänomenen begleitet. Zur besseren Modellierung dieser Erscheinungen wurde im Vorjahr (vgl. [7, 8, 9] ) ein neuer Zugang entwickelt, der darin besteht, die Hysterese direkt in Form von Hysterese-Operatoren in die Phasenfeldgleichungen aufzunehmen. Man erhält dabei Systeme der Form
$\begin{align} \mu(\theta)\,w_t\,+\,{\cal H}_1 [w]\,+\,{\cal H}_2 [w]\,\theta\,&=... ...F}_1 [w]\right)_t\,-\,\kappa\,\Delta \theta\,&=\,g (\theta, x, t)\,,\end{align}$
wobei $\,{\cal H}_1\,,\, {\cal H}_2\,,\, {\cal F}_1\,$ geeignete Hysterese-Operatoren sind.

Motiviert wurde dieser Zugang dadurch, daß sich Modellierungen mit Hilfe von Variationsungleichungen, wie z. B. das klassische relaxierte Stefan-Problem, auf die Form (8), (9) transformieren lassen. Dabei sorgt die vorausgesetzte Dissipativität der Hysterese-Operatoren $\,{\cal H}_1\,,\, {\cal H}_2\,$ dafür, daß der Zweite Hauptsatz der Thermodynamik in Form der Entropieungleichung erfüllt ist.

Es gelang im Berichtszeitraum, die in [7, 8, 9] erzielten Resultate auf wesentlich allgemeinere Situationen auszudehnen. Die Ergebnisse sind in den Arbeiten [3] und [10] zusammengefaßt.

Projektliteratur:

P. COLLI, M. FRéMOND, O. KLEIN, Global existence of a solution to a model for supercooling, in Vorbereitung.
M. FRéMOND, A macroscopic predictive theory of supercooling, in: Trends in Applications of Mathematics to Mechanics (M. M. Marques, J. F. Rodrigues, Hrsg.), Longman, 1995.
G. GILARDI, P. KREJCí, J. SPREKELS, A hysteresis approach to phase-field models with memory, in Vorbereitung.
O. KLEIN, Existence and Approximation Results for Phase-Field Systems of Penrose-Fife Type and Stefan Problems, Dissertation, Humboldt-Universität zu Berlin, ISBN 3-8265-3056-X.
$\dito$ ,A phase-field system with space-dependent relaxation coefficient, erscheint in: Free Boundary Problems, Theory and Applications, Proceedings of the Crete Congress 97 (I. Athanasopoulus, G. Makrakis, J. F. Rodriquez, Hrsg.), Pitman Research Notes in Mathematics, CRC press.
$\dito$ , A class of time discrete schemes for a phase-field system of Penrose-Fife type , WIAS-Preprint No. 424, 1998, eingereicht.
P. KREJCí, J. SPREKELS, A hysteresis approach to phase-field models , WIAS-Preprint No. 364, 1997, erscheint in: Nonlin. Anal. TMA.
$\dito$ ,Hysteresis operators in phase-field models of Penrose-Fife type , Appl. Math., 43 (1998), pp. 207-222.
$\dito$ ,Hysteresis operators in phase-field models, in: Topics in Nonlinear Analysis - The Herbert Amann Anniversary Volume (J. Escher, G. Simonett, Hrsg.), Birkhäuser Verlag, Basel, 1999, pp. 499-516.
$\dito$ ,Phase-field models with hysteresis , WIAS-Preprint No. 458, 1998, eingereicht.
R. H. NOCHETTO, G. SAVARé, C. VERDI, A posteriori error estimates for variable time-step discretizations of nonlinear evolution equations, Mittag-Leffler-Institut, Preprint 20, 1997/98.
O. PENROSE, P. C. FIFE, Thermodynamically consistent models of phase-field type for the kinetics of phase transitions, Physica D, 43 (1990), pp. 44-62.