Rekonstruktion aus zeitaufgelösten Messungen in der

[Next]:

Zur Asymptotik von Paardiffusionsmodellen

[Up]:

Projektbeschreibungen

[Previous]:

Lineare elliptische Randwertprobleme mit nichtglatten Daten:

[Contents]

[Index]

Rekonstruktion aus zeitaufgelösten Messungen in der optischen Tomographie

Bearbeiter: R. Hünlich

Kooperation: R. Model, M. Orlt, M. Walzel (Physikalisch-Technische Bundesanstalt Berlin-Charlottenburg)

Beschreibung der Forschungsarbeit: Ziel der Untersuchungen in [4] war es, die im Rahmen eines inzwischen abgeschlossenen BMBF-Projekts [2] entwickelten Verfahren zur Bildrekonstruktion in der optischen Tomographie, die auf zeitaufgelösten Messungen beruhen (siehe auch [3]), an dem Standarddatensatz der Universität von Pennsylvania [1] zu testen.

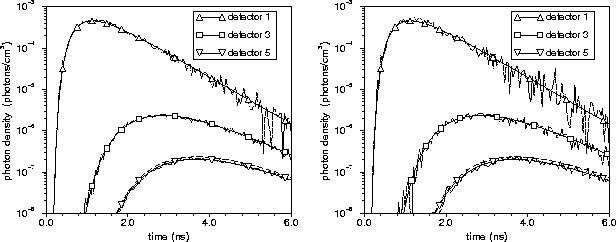
$\begin{figure} \ProjektEPSbildNocap {1.0\textwidth}{fb98_hue_bild5.eps} \end{figure}$

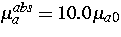Abb. 1: Rekonstruktionsergebnisse für den zehnfachen Absorber ( $\mu_a^{abs}=10.0\,\mu_{a0}$ ). Die Bilder zeigen einen Vergleich zwischen den Photonendichten des verrauschten Standarddatensatzes (links 5%, rechts 10% Rauschen) und den simulierten Photonendichten nach Rekonstruktion des Absorbers. Zur Rekonstruktion wurde eine Meßanordnung wie in [5, Abb. 2] benutzt. 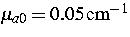Zum Vergleich sind auch die Photonendichten für das homogene Medium ( $\mu_{a0}=0.05\,\mbox{cm}^{-1}$ ) gezeichnet (gestrichelt), wobei deutlichere Abweichungen nur für Detektor 5 zu erkennen sind.

Meßanordnung, Datensatz, das entwickelte Rekonstruktionsverfahren (least-squares Methode unter Benutzung einer 2D-FEM-Vorwärtsrechnung mit anschließender 3D-Korrektur) sowie erste Ergebnisse wurden in [5] beschrieben. Darauf aufbauend wurde nun der Einfluß eines auf die Daten aufgeprägten Rauschens untersucht. Es zeigte sich, daß vor allem bei stärkerem Rauschen der volle Datensatz (12 Lichtquellen mit jeweils 10 Detektoren) herangezogen werden mußte, um erfolgreich rekonstruieren zu können. In Abb. 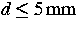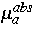2 wird dargestellt, wie die Güte der Rekonstruktion (es sollte $d\le 5\,\mbox{mm}$ sein) von der Rauschstärke und dem Absorptionskoeffizienten $\mu_a^{abs}$ der Inhomogenität abhängt. Bei stärkerem Rauschen führt eine Datenfilterung zu einer erheblichen Verbesserung der Ergebnisse, vor allem bei Verwendung eines reduzierten Datensatzes mit weniger Lichtquellen und Detektoren.

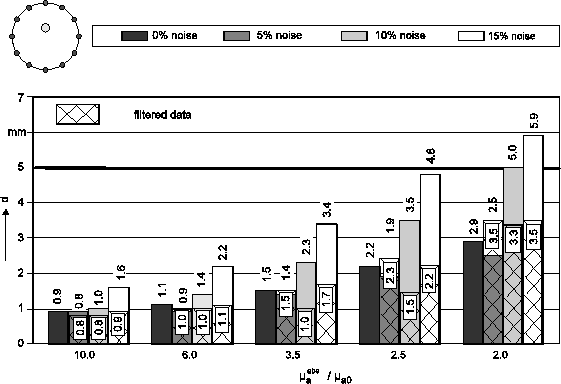
$\begin{figure} \ProjektEPSbildNocap {0.9\textwidth}{fb98_hue_bild6.eps} \end{figure}$

Abb. 2: Rekonstruktionsergebnisse bei verrauschten Daten. Dargestellt ist der Abstand d zwischen den Mittelpunkten des identifizierten und vorgegebenen Absorbers (mit 5mm Radius) in Abhängigkeit vom Absorptionskoeffizienten und der Stärke des Rauschens.

Projektliteratur:

D. BOAS, Time-domain standard data series, University of Pennsylvania, URL http://www.
lrsm.upenn.edu.
R. MODEL, M. ORLT, M. WALZEL, R. HÜNLICH, Mathematische Behandlung der Streulichttomographie von dicken Gewebeschichten und Phantomen, Lasermedizinforschung, Projekte im Schwerpunkt ,,Lasermedizin``, BMBF-Förderkonzept LASER 2000, VDI Technologiezentrum Physikalische Technologien, Düsseldorf, 1997, pp. 130-132.
$\dito$ , Reconstruction algorithm for near-infrared imaging in turbid media by means of time-domain data, Optical tomography. Fundamentals and applications in medicine (O. Minet, G. Müller, J. Beuthan, Hrsg.), SPIE Milestone Series, vol. MS 147, SPIE Optical Engineering Press, Bellingham, 1998, pp. 537-548.
$\dito$ , Optical imaging: Three dimensional approximation and perturbation approaches for time-domain data, Applied Optics, 37 (1998), pp. 7968-7976.
Weierstraß-Institut für Angewandte Analysis und Stochastik, Jahresforschungsbericht 1996, pp. 30-31.