Bearbeiter:
R. Hünlich
,
A. Glitzky
,
W. Röpke
Kooperation: N. Strecker (Eidgenössische Technische Hochschule Zürich),
W. Merz, K. Pulverer (Technische Universität München)
Förderung: DFG: ,,Analytische Untersuchungen von
Elektro-Reaktions-Diffusionsgleichungen mit nichtglatten Daten``, BMBF
Beschreibung der Forschungsarbeit:
Die bei der Simulation von Halbleitertechnologien
vorrangig benutzten
Diffusionsmodelle
reichen bei modernen Bauelementen nicht mehr aus, um alle
Transportphänomene adäquat zu beschreiben.
Von Bedeutung sind
Untersuchungen zu neuartigen Materialien (siehe z.B.
[10]) sowie die Diskussion
verschiedener Varianten von Paardiffusionsmodellen
(siehe [1, 6, 11]),
die die Kinetik von
Eigenpunktdefekten
und von
Fremdatom-Defekt-Paaren
in verschiedenen Ladungszuständen genauer
modellieren sollen.
Gleichungen zu Paardiffusionsmodellen reduzieren sich
unter der
Annahme, daß alle Ionisierungsreaktionen
sowie die Kinetik der Elektronen und Löcher sehr schnell sind,
auf einen aus Sicht der
Simulation erträglichen Umfang.
Erste Aussagen zur Analysis und Numerik dieser Modellklasse findet man in
[8, 9]. In [5, 7]
haben wir weiterführende Ergebnisse erzielt, die im folgenden
zusammengestellt werden sollen.
Abb. 1:
Reaktionen im Paardiffusionsmodell
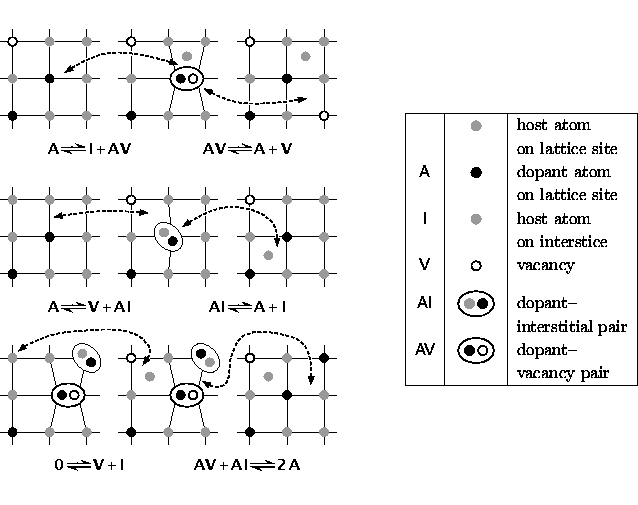 |
Die Modellgleichungen bestehen aus allgemein m
(im Fall,
daß nur ein Dotand A
vorliegt, fünf)
Kontinuitätsgleichungen
für die Konzentrationen
ui der Spezies i (nämlich 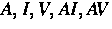 ;
siehe Abb. 1), die mit
einer nichtlinearen Poissongleichung
zur Bestimmung des chemischen
Potentials der Elektronen
;
siehe Abb. 1), die mit
einer nichtlinearen Poissongleichung
zur Bestimmung des chemischen
Potentials der Elektronen 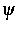 gekoppelt sind:
gekoppelt sind:
| 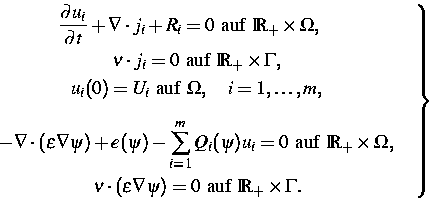 |
(3) |
Die Stromdichten
ji sind durch
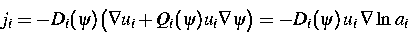
gegeben, mit Ri bezeichnen wir die Raten der
einzelnen Paarbildungs- bzw. Generations-Rekombinations-Reaktionen:
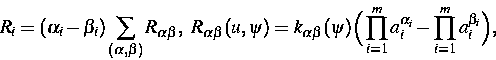
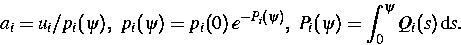
Die Ladungszahlen Qi und die kinetischen Koeffizienten 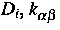 hängen von
hängen von 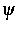 ab,
ab, 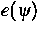 ist durch den
Statistikansatz für die Elektronen gegeben, ferner sei
ist durch den
Statistikansatz für die Elektronen gegeben, ferner sei
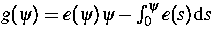 .
.
Modelle, bei denen die
Ladungszahlen Qi (und Diffusionskoeffizienten Di) nicht von
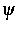 abhängen, haben wir früher behandelt
(siehe [2, 3, 4]).
Das Auftreten dieser zusätzlichen
Abhängigkeiten macht die Aufgabe wesentlich komplizierter,
hinzu kommt, daß man (im Unterschied zu [9])
für einige Spezies (den Dotanden A)
Di=0 anzunehmen
hat.
abhängen, haben wir früher behandelt
(siehe [2, 3, 4]).
Das Auftreten dieser zusätzlichen
Abhängigkeiten macht die Aufgabe wesentlich komplizierter,
hinzu kommt, daß man (im Unterschied zu [9])
für einige Spezies (den Dotanden A)
Di=0 anzunehmen
hat.
Ausgangspunkt unserer Untersuchungen sind energetische Abschätzungen
(in zwei Raumdimensionen),
die einerseits zeigen, daß die Modellgleichungen aus thermodynamischer
Sicht korrekt formuliert sind, die andererseits die Grundlage für
weitere a priori-Abschätzungen
und damit verbundene Existenzaussagen
bilden sollten, mit denen wir uns zukünftig befassen werden.
Es bezeichne 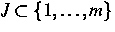 die Teilmenge der
diffundierenden Spezies (der Punktdefekte und Paare
die Teilmenge der
diffundierenden Spezies (der Punktdefekte und Paare
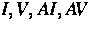 ).
Wir definieren ein Energiefunktional
).
Wir definieren ein Energiefunktional
![\begin{displaymath}
F(u)=
\int_\Omega\Big\{\frac{\varepsilon}{2}\vert\nabla\psi\...
...Big[\ln\frac{u_i}{p_i(0)}-1\Big]+p_i(0)\Big\}
\Big\}\,\text dx,\end{displaymath}](../../1998/html/images/img88.gif)
wobei
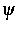 Lösung der Poissongleichung ist,
sowie ein
Dissipationsfunktional
Lösung der Poissongleichung ist,
sowie ein
Dissipationsfunktional
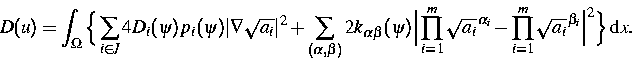
Wir haben nachgewiesen, daß
für jede schwache Lösung von (1)
die Relation
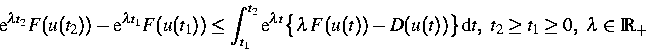
gilt.
Aus dieser Abschätzung folgt, daß die Energie
längs Trajektorien der Aufgabe (1) beschränkt bleibt und
monoton fällt.
Weiterhin gibt es zu jedem R>0 ein cR>0, so daß
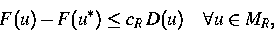
wobei
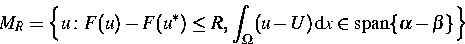
und u* der durch
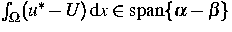 eindeutig bestimmte stationäre Zustand
von (1) ist.
Zusammen mit dem ersten Ergebnis folgt hieraus, daß die Energie
entlang von schwachen Lösungen des Systems (1)
für
eindeutig bestimmte stationäre Zustand
von (1) ist.
Zusammen mit dem ersten Ergebnis folgt hieraus, daß die Energie
entlang von schwachen Lösungen des Systems (1)
für 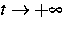 exponentiell gegen ihren
Gleichgewichtswert
strebt.
exponentiell gegen ihren
Gleichgewichtswert
strebt.
Abschließend sei erwähnt, daß wir analog zu dem Vorgehen in
[2] auch für Zeitdiskretisierungen
von (1)
energetische Abschätzungen
erhalten haben, die Aussagen
über die Stabilität des Näherungsverfahrens nach sich ziehen.
Projektliteratur:
- S. T. DUNHAM, A quantitative model for the coupled diffusion of
phosphorus and point defects in silicon, J. Electrochem.
Soc., 139 (1992), pp. 2628-2636.
- A. GLITZKY, R. HÜNLICH, Energetic estimates and asymptotics for
electro-reaction-diffusion systems, Z. Angew. Math. Mech.,
77 (1997), pp. 823-832.
-
 , Global estimates and asymptotics for electro-reaction-diffusion
systems in heterostructures, Appl. Anal., 66 (1997),
pp. 205-226.
, Global estimates and asymptotics for electro-reaction-diffusion
systems in heterostructures, Appl. Anal., 66 (1997),
pp. 205-226.
-
 , Electro-reaction-diffusion systems including cluster reactions
of higher order, erscheint in: Math. Nachr.
, Electro-reaction-diffusion systems including cluster reactions
of higher order, erscheint in: Math. Nachr.
-
 , Energy estimates for
electro-reaction-diffusion systems with partly fast kinetics, in
Vorbereitung.
, Energy estimates for
electro-reaction-diffusion systems with partly fast kinetics, in
Vorbereitung.
- A. HÖFLER, Development and application of a model hierarchy
for silicon process simulation, Series in Microelectronics,
vol. 69, Hartung-Gorre, Konstanz, 1997.
- R. HÜNLICH, A. GLITZKY, On energy estimates for electro-diffusion
equations arising in semiconductor technology,
erscheint in: Proceedings PDE Prague'98.
- J. LANG, W. MERZ, Numerical simulation of single species dopant
diffusion in silicon under extrinsic conditions, Preprint SC 97-47,
Konrad-Zuse-Zentrum für Informationstechnik Berlin, 1997.
- W. MERZ, Analysis und numerische Berechnung der Diffusion von
Fremdatomen in homogenen Strukturen, Habilitationsschrift, Technische
Universität München, 1998.
- H. RÜCKER, B. HEINEMANN, W. RÖPKE, R. KURPS, D. KRÜGER, G. LIPPERT, H. J. OSTEN, Suppressed diffusion of boron and carbon
in carbon-rich silicon, Appl. Physics Lett., 73 (1998),
pp. 1682-1684.
- N. STRECKER,
ISE TCAD manuals. Release 4.0. Part 8: DIOS-ISE,
Integrated Systems Engineering AG, Zurich, 1997.
LaTeX typesetting by I. Bremer
7/30/1999

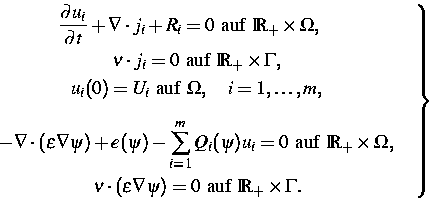
![]()
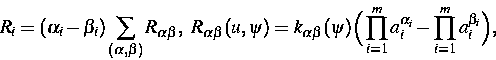
![]()
![]() abhängen, haben wir früher behandelt
(siehe [2, 3, 4]).
Das Auftreten dieser zusätzlichen
Abhängigkeiten macht die Aufgabe wesentlich komplizierter,
hinzu kommt, daß man (im Unterschied zu [9])
für einige Spezies (den Dotanden A)
Di=0 anzunehmen
hat.
abhängen, haben wir früher behandelt
(siehe [2, 3, 4]).
Das Auftreten dieser zusätzlichen
Abhängigkeiten macht die Aufgabe wesentlich komplizierter,
hinzu kommt, daß man (im Unterschied zu [9])
für einige Spezies (den Dotanden A)
Di=0 anzunehmen
hat.
![]() die Teilmenge der
diffundierenden Spezies (der Punktdefekte und Paare
die Teilmenge der
diffundierenden Spezies (der Punktdefekte und Paare
![]() ).
Wir definieren ein Energiefunktional
).
Wir definieren ein Energiefunktional
![\begin{displaymath}
F(u)=
\int_\Omega\Big\{\frac{\varepsilon}{2}\vert\nabla\psi\...
...Big[\ln\frac{u_i}{p_i(0)}-1\Big]+p_i(0)\Big\}
\Big\}\,\text dx,\end{displaymath}](../../1998/html/images/img88.gif)
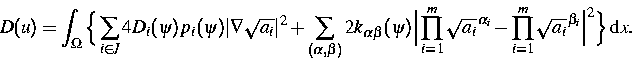
![]()
![]()
![]()