Theoretische Untersuchungen zum Stabilitätsverhalten von Verdichtern

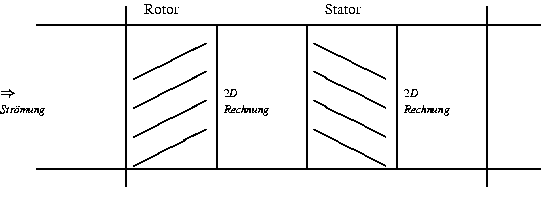
Verdichter als Teile von Flugtriebwerken haben die Aufgabe, mittels eines Rotors kinetische Energie auf das Gas zu übertragen, was durch die Wirkung des Stators eine Erhöhung der Enthalpie und des Drucks zur Folge hat. Ein zentrales Problem bei der Entwicklung von Verdichtern ist es, das Auftreten von Strömungsinstabilitäten zu modellieren und vorherzusagen, da sie zu einer Verringerung des Wirkungsgrades oder zur Zerstörung des Verdichters führen können. Gegenstand des Projektes sind numerische Untersuchungen solcher Instabilitäten in Verdichtern. Es wurde ein Modell entwickelt, in dem die Strömung im unbeschaufelten Gebiet durch die 2D-Euler-Gleichungen der Gasdynamik simuliert wird. Zur Kopplung der verschiedenen Teile des Verdichters, die durch den Einfluß von Rotor und Stator charakterisiert ist, wurden Übergangsbedingungen mit Hilfe von Erhaltungsgleichungen und Quelltermen aus Verdichterkennlinien formuliert. Diese Übergangsbedingungen berücksichtigen die Effekte der Viskosität. Am Eintritt und Austritt des Verdichters sind nichtreflektierende Randbedingungen benutzt worden (Giles [1]), um nichtphysikalische Reflektionen am Rand zu vermeiden. Das in diesem Projekt entwickelte Modell ist in der Lage, verschiedene Strömungszustände durch Veränderung eines einzigen Parameters, nämlich des Austrittsdrucks, zu erzeugen.

Für die numerische Berechnung der Strömung in den unbeschaufelten Gebieten des Modells wurde ein Godunov-Verfahren mit einem Roe-Solver von LeVeque [2] benutzt. Die Strömung ist in einem zweistufigen Verdichter untersucht worden. Das Rechengebiet besteht aus fünf unbeschaufelten Gebieten, am Eintritt und hinter jedem Rotor bzw. Stator (siehe Abb. 1).

**Abb. 1:** Schematische Darstellung einer Verdichterstufe
$\ProjektEPSbildNocap {12cm}{fb98_1_sch_bild1.eps}$

Das Lösungsverhalten des Modells ist durch die Werte für Dichte, Geschwindigkeit und Druck am Eintritt und Austritt des Verdichters, über die die Euler-Gleichungen zur Formulierung nichtreflektierender Randbedingungen linearisiert wurden, bestimmt. Für einen gegebenen Massenstrom sind die Werte dieser Variablen durch die Verdichtercharakteristik gegeben. Ausgehend von diesen Werten für einen bestimmten Massenstrom wurde das Lösungsverhalten des Modells durch Erhöhung des Drucks $\hat{p}_{r}$ am Austritt gesteuert. Mit wachsendem Austrittsdruck verliert eine anfangs stabile stationäre Lösung ihre Stabilität in einer Hopfbifurkation an verschiedene koexistierende, zeitlich periodische Lösungen mit unterschiedlich vielen rotierenden Ablösezellen (rotierende Ablösung), gefolgt von Lösungen mit einer zeitlichen Änderung des Drucks in den Ablösezellen (rotierende Instabilität). Während für diese zeitlich periodischen Zustände der Massenstrom zeitunabhängig ist, wird der Massenstrom zeitabhängig (Pumpen), falls der Austrittsdruck hinreichend groß ist. Ein Überblick über die verschiedenen Lösungszweige ist schematisch in Abb. 2 dargestellt.

**Abb. 2:** Schematisches Bifurkationsdiagramm
$\ProjektEPSbildNocap {12cm}{fb98_1_sch_bild2.eps}$

Für $\hat{p}_{r}=167400$ Pa existiert eine stabile stationäre Lösung, d. h. alle Trajektorien werden von dieser Lösung angezogen. Der Zustand des Systems konvergiert gegen eine Lösung, die in jedem einzelnen Rechengebiet zeitlich und räumlich konstant ist. Falls der Austrittsdruck einen kritischen Wert, $\hat{p}_{r}\approx170000$ Pa, übersteigt, entsteht eine periodische Lösung mit zwei rotierenden Ablösezellen in jedem einzelnen Rechengebiet des Modells. In Abb. 3 ist der Druck in den fünf unbeschaufelten Gebieten des Verdichters zu einem Zeitpunkt für $\hat{p}_{r}=172160$ Pa gegeben. In jedem einzelnen Gebiet entstehen zwei Ablösezellen, die sich in Umfangsrichtung bewegen. In Abb. 4 ist die Instabilität der stationären Lösung demonstriert. Der Druck über dem Umfang am Austritt des Verdichters ist als Funktion der Zeit gegeben. Der Zustand des Systems verläßt den ursprünglich stationären Zustand und konvergiert gegen die neue Lösung mit zwei Ablösezellen.

Bei einer Erhöhung des Austrittsdrucks entstehen neue Lösungszweige mit drei und vier Ablösezellen. Der Zweig mit zwei Zellen bleibt stabil. Damit koexistieren drei stabile periodische Lösungen. Die Drehrichtung der Zellen entspricht der Drehrichtung des Rotors, und die Rotationsfrequenz der Zellen beträgt ca. 150 Hz.

**Abb. 3:** Druck im Verdichter für eine periodische Lösung mit 2 rotierenden Ablösezellen in jedem unbeschaufelten Gebiet, die sich in Umfangsrichtung
bewegen, $\hat{p}_{r}=172160$ Pa
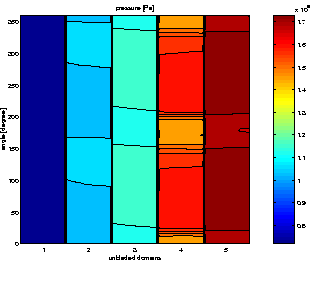
$\ProjektEPSbildNocap {7cm}{fort_250.eps}$

**Abb. 4:** Druck am Verdichteraustritt als Funktion der Zeit, $\hat{p}_{r}=172160$ Pa
$\ProjektEPSbildNocap {7cm}{fort_300.eps}$

**Abb. 5:** Druck am Verdichteraustritt als Funktion der Zeit, $\hat{p}_{r}=199740$ Pa
$\ProjektEPSbildNocap {7cm}{press.ps}$

Für $\hat{p}_{r}\approx199740$ Pa verschwinden die periodischen Lösungen mit Ablösezellen, und es entsteht eine neue Lösung mit zwei Zellen, deren Druck sich jetzt zeitlich ändert (siehe Abb. 5). Der Massenstrom bleibt zeitunabhängig. Diese rotierende Instabilität wurde bereits von Kameier [3] sowie von Mailach et al. [4] experimentell beobachtet. Wenn der Austrittsdruck weiter erhöht wird, $\hat{p}_{r}\geq205110$ Pa, werden alle Lösungszweige mit Ablösezellen instabil, und es entsteht eine Lösung mit einer zeitlichen Änderung des Massenstroms. In Abb. 6 und Abb. 7 ist der über den Umfang gemittelte Druck und der Massenstrom am Austritt des Verdichters als Funktion der Zeit gegeben. Der Anstieg des Drucks ist mit einem Abfall des Massenstroms gekoppelt, der Massenstrom wird negativ, gefolgt von einer Periode regulären Verhaltens bis der nächste Pumpstoß beginnt. Die Pumpfrequenz beträgt etwa 5 Hz, was mit gemessenen Werten übereinstimmt.

**Abb. 6:** Umfangsgemittelter Druck am Verdichteraustritt als Funktion der Zeit, $\hat{p}_{r}=205110$ Pa
$\ProjektEPSbildNocap {7cm}{press70.ps}$

**Abb. 7:** Massenstrom als Verdichteraustritt als Funktion der Zeit, $\hat{p}_{r}=205110$ Pa
$\ProjektEPSbildNocap {7cm}{mass70.ps}$

Dieser Übergang zum Pumpen ähnelt einem Schema, das bereits von Day [5] gefunden wurde, d. h. das Pumpen erscheint nach einem Strömungszustand mit rotierender Ablösung. Außerdem ist der Weg zum Pumpen ähnlich dem Übergang zu irregulärem Verhalten, das aus vielen Beispielen in der Hydrodynamik bekannt ist. Ein anfangs stabiler stationärer Zustand verliert seine Stabilität an eine periodische Lösung, gefolgt von einer quasiperiodischen Lösung mit zwei beteiligten Frequenzen und schließlich irregulärem turbulentem Verhalten.