Bandstrukturberechnungen für Quantum Wells in Halbleiter-Heterostrukturen

Kooperation: Bosch Telecom GmbH, H. Wenzel (Ferdinand-Braun-Institut für Höchstfrequenztechnik Berlin), H.-J. Wünsche (Institut für Physik, Humboldt-Universität zu Berlin)

Die kp-Methode ist ein etabliertes Standardmodell zur Berechnung der Bandstruktur von Halbleitermaterialien [1], siehe 4.1.2. Diese Methode ist unabhängig von der Zahl der Atome und macht nur von Bandstrukturdaten der beteiligten Volumenmaterialien Gebrauch. In der Enveloppenfunktionsapproximation eignet sie sich darüber hinaus zur Behandlung von ggf. mechanisch verspannten Heterostrukturen, z. B. Quantum Wells.

Physikalisches Modell.

Die kp-Methode im Volumenmaterial beruht auf einer störungstheoretischen Beschreibung der Bandstruktur $E(\vec{k})$ im Rahmen einer Basis als physikalisch relevant identifizierter Bandkanten-Blochfunktionen. Diese führt auf matrixwertige Eigenwertprobleme für $E(\vec{k})$ , die parametrisch vom Wellenvektor $\vec{k}$ abhängen.

In Heterostrukturen führt der Verlust der Translationssymmetrie zu einer Aufspaltung in Subbänder. Weitere Effekte wie Spin-Bahn-Wechselwirkung und mechanische Verspannung bewirken zusätzliche Aufspaltungen. Die Wellenfunktionen in der Heterostruktur werden durch Enveloppenfunktionen approximiert, die Eigenfunktionen von matrixwertigen Hamiltonoperatoren sind. Letztere hängen parametrisch vom reduzierten Wellenvektor $\vec{k}_\Vert$ ab. Dabei werden die Daten für die einzelnen beteiligten Materialien aus denen der entsprechenden Volumenmaterialien übernommen, was zu springenden Koeffizienten in den Hamiltonoperatoren führt. Speziell für Quantum Wells ergeben sich daraus räumlich eindimensionale matrixwertige Hamiltonoperatoren.

Mathematische Analyse.

Im Rahmen des Projektes wurde eine funktionalanalytische Untersuchung [2] für eindimensionale kp-Operatoren durchgeführt. Hierbei wurden kp-Operatoren mit stückweise konstanten Koeffizienten betrachtet. Von Interesse waren einerseits Aussagen über die spektralen Eigenschaften der einzelnen Operatoren und andererseits über die Abhängigkeit dieser spektralen Eigenschaften vom Wellenvektor $\vec{k}_\Vert$ . Aus physikalischer Sicht stellte sich insbesondere die Frage nach der Erhaltung einer bei $\vec{k}_\Vert=0$ vorhandenen spektralen Lücke für endliche Werte von $\vec{k}_\Vert$ sowie diejenige nach globaler Existenz von Eigenwertkurven $E(\vec{k}_\Vert)$ . Erstere konnte unter Ausnutzung von Struktureigenschaften der Koeffizientenmatrizen positiv beantwortet werden, dabei gelangen sogar quantitative Abschätzungen in den Daten des Problems. An spektralen Eigenschaften konnten Selbstadjungiertheit und Nuklearität der Resolvente bewiesen werden. Von den Eigenwertkurven wurde Analytizität gezeigt, hingegen gelang der Beweis globaler Existenz nur für ein in den Koeffizienten erster Ordnung regularisiertes Problem, welches das ursprüngliche allerdings spektral beliebig genau zu approximieren gestattet.

Numerisches Verfahren.

Zur numerischen Lösung des Problems wurde ein Finite-Elemente-Ansatz verwendet. Dieser wird durch die mathematische Analyse der Operatoren nahegelegt. Numerische Untersuchungen an einem analytisch lösbaren Testproblem haben für diese Methode in den Eigenwerten eine Konvergenz der Ordnung ${\cal O}(h^2)$ belegt. Diese h²-Konvergenz konnte für ein physikalisches Testproblem (siehe Abb. 1) für zwei schwere und zwei leichte Löcher ( $4 \times 4$ Hamiltonian nach Chuang [1]) mit springenden Koeffizienten bestätigt werden (siehe Abb. 2). Über den Bereich der gesamten Brillouin-Zone erwies sich das Verfahren als stabil.

Das Verfahren zur Diskretisierung und Lösung des Eigenwertproblems wurde mit pdelib-Komponenten (siehe S.

) realisiert und steht in Form der Problembeschreibungsklasse kplib zur Verfügung. Zusätzlich wurde über eine Anbindung der kplib an die Skriptsprache lua ein komfortabler, leicht erweiterbarer Simulator realisiert. Der Code kplib kann als Ausgangsbasis für weitere kp-Modelle dienen.

**Abb. 1:** Subbandstruktur für schwere Löcher (HH) und leichte Löcher (LH) für einen 51Å dicken AlGaAs/GaAs Quantum Well für jeweils $\vec{k}_\Vert=[100]$ und $\vec{k}_\Vert=[110]$ -Richtung. Nichtparabolizität und Warping (Richtungsabhängigkeit der Energie) sind deutlich zu sehen.
$\ProjektEPSbildNocap {5.9cm}{bandstructure-jfb-98.eps}$

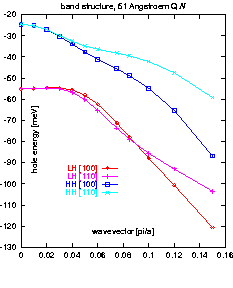
**Abb. 2:** Relativer Fehler der Eigenwerte in Abhängigkeit von der Anzahl der Gitterpunkte im Quantum Well mit äquidistantem Gitter für verschiedene Beträge und Richtungen von $\vec{k}_\Vert$ . Es ist eine strikte h²-Konvergenz zu beobachten.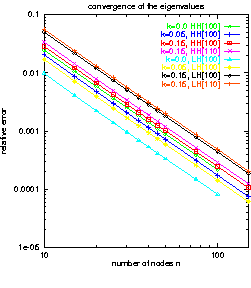
$\ProjektEPSbildNocap {5.9cm}{conv-jfb-98.eps}$