Approximation und Optimierung von Platten

Bearbeiter: H. Langmach (FG 3) , J. Sprekels (FG 1) , D. Tiba (Rumänische Akademie der Wissenschaften)  

Kooperation: V. Arnautu (University of Iasi, Dept. of Mathematics, Rumänien, z. Zt. WIAS)

Förderung: Alexander von Humboldt-Stiftung

Beschreibung der Forschungsarbeit: Die Auslenkung einer dünnen Platte unter Einwirkung einer Kraft f=f(x₁,x₂) wird durch die Lösung y=y(x₁,x₂) eines Randwertproblems zur biharmonischen Gleichung  

$$\Delta (u^3\,\Delta y)\,=\,f \quad \mbox{in } \Omega \subset \IR^2$$ (1)

beschrieben, wobei u=u(x₁,x₂) die Dicke der Platte bedeutet. Als Randbedingung treten dabei folgende Fälle auf:

    $$\begin{eqnarray} y\,=& \Delta y &=\,0 \quad \mbox{auf }\partial \Omega \qqua... ...ox{auf } \partial \Omega \qquad\mbox{\rm (eingespannte Platte)}.\end{eqnarray}$$

Es wurde eine neue Methode zur Approximation und Optimierung von Platten erarbeitet, die auf der Dekomposition des Randwertproblems (1), (2) bzw. (1), (3) zur biharmonischen Gleichung in zwei elliptische Randwertprobleme beruht, die als Nebenbedingungen in ein Problem der Optimalen Steuerung eingehen. Dabei wird die Einhaltung der Randbedingungen für die Platte mittels eines im Zielfunktional aufgenommenen Strafterms erreicht. Neben dem Randwertproblem für die Platte wurde auch eine daraus abgeleitete Variationsungleichung behandelt. Die Konvergenz des Strafverfahrens konnte für beide Fälle unter allgemeinen Voraussetzungen bewiesen werden.

Der gewählte Zugang eröffnet die Möglichkeit, die Lösung des Problems mit Hilfe stückweise linearer finiter Elemente zu approximieren, die leicht implementiert werden können.

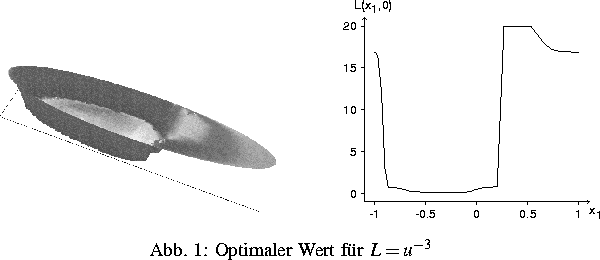
Im Zusammenhang mit der Optimierung von Platten wurden u. a. Probleme betrachtet, bei denen die zu optimierende Größe von der lokalen Dicke u der Platte abhängt (Minimierung des Volumens, optimal shape design). Die folgende Abbildung zeigt die Funktion L=u^-3 nach Minimierung des Volumens $\int_\Omega u(x_1,x_2) dx_1 dx_2 \quad$der Platte bei vorgegebenen Restriktionen an L unter unsymmetrischer Last f.

Für die Lösung der in den genannten Problemklassen als Nebenbedingungen auftretenden elliptischen Randwertprobleme wurden die im WIAS entwickelten Softwarekomponenten pdelib (siehe S. ) eingesetzt.

Projektliteratur:

1. V. ARNAUTU, H. LANGMACH, J. SPREKELS, D. TIBA, On the approximation and optimization of plates, WIAS-Preprint No. 357 (1997).
2. J. SPREKELS, D. TIBA, A duality approach in the optimization of beams and plates, WIAS-Preprint No. 335 (1997), eingereicht.