Komponenten für die Data Mining Software Clementine

 Bearbeiter: J. Fuhrmann (FG 3) , H.-J. Mucha (FG 6) , G. Reinhardt (FG 3)  

Kooperation: C. Steinborn (FU), U. Grimmer, G. Nakhaeizadeh, H. Kauderer (Forschungszentrum Daimler-Benz AG, Ulm)

Beschreibung der Forschungsarbeit:

3D-Dichteschätzung.

Zur Suche nach Strukturen und Anomalien in umfangreichen Datensammlungen können effektive Techniken der Clusteranalyse (automatische Klassifikation) eingesetzt werden. Zum besseren Verständnis von Daten und/oder Klassifikationsergebnissen können mehrdimensionale Dichteschätzungen hilfreich und bestens geeignet sein. Geeignet deshalb, weil bei Massendaten die Bedeutung eines einzelnen Objektes (Punktes im hochdimensionalen Raum) gegen Null geht und die üblichen Punkte-Plots schwer lesbar und auch rechentechnisch uneffektiv werden.

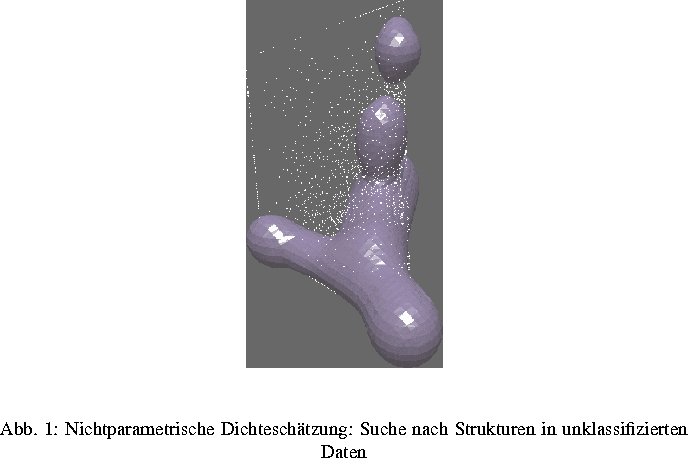
Im allgemeinen werden der nichtparametrischen Dichteschätzung geeignete Projektionstechniken vorangestellt, die möglichst viele Informationen des hochdimensionalen Beobachtungsraumes in einen niedrigdimensionalen Unterraum abbilden. Die adaptive Clusteranalyse kann die zur Struktursuche geeigneten Projektionsparameter berechnen.

Die Software wurde auf der Grundlage der OpenGL-basierten Toolbox gltools des WIAS entwickelt. Es können nichtparametrische Dichteschätzungen von unklassifizierten oder gruppierten Daten angezeigt werden. Interaktive Aktionen wie z. B. Drehungen und intuitive Bedienungsweisen erlauben eine schnelle Information des Benutzers über die Konturen der Punktwolken.

Algorithmen für die partitionierende Clusteranalyse.

Für die Clusterung von Daten wurden für eine vom Forschungszentrum der Daimler-Benz AG in Ulm vorgegebene Datenstruktur der L1- und L2-Algorithmus angepaßt und implementiert. Die Datenstruktur ist für Variablen vorgesehen, die quantitative, ordinale (ganzzahlig) und binäre Werte annehmen können. Qualitative Daten (symbolische Werte wie z. B. die Haarfarben ,,braun``, ,,blond`` und ,,schwarz`` oder nominale ganzzahlige Werte wie z. B. die Kodierung 1, 2, ... für den Familienstand einer Person) können vor der Clusteranalyse in binäre Variablen rekodiert werden.

Beim L1-Algorithmus ist der Repräsentant eines Clusters aus den Medianen der einzelnen Variablen zu bestimmen. Durch eine Modifikation des quick-sort-Algorithmus (C. A. R. Hoare) gelingt es, den Median mit linearem Aufwand von O(n_K) zu bestimmen (n_K = Anzahl der Variablen pro Cluster K). Damit liegt der Aufwand zur Bestimmung der Repräsentanten des L1-Algorithmus in der gleichen Größenordnung wie beim L2-Algorithmus, bei dem der Repräsentant eines Clusters aus den Mittelwerten der Attribute gewählt wird.

Allerdings muß beachtet werden, daß beim L1-Algorithmus ein Repräsentant durch Speicheroperationen (Sortieren) ermittelt wird, während beim L2-Algorithmus dies schnelle arithmetische Operationen sind.

Durch die Aufwandsreduzierung bei der Bestimmung der Repräsentanten wird der L1-Algorithmus für die Verarbeitung großer Datenmengen praktisch relevant. Da beim L1-Algorithmus nur absolute Differenzen benutzt werden (im Gegensatz zu den quadrierten Differenzen beim L2-Algorithmus), beeinflussen Ausreißer in den Daten weniger stark das Klassifikationsergebnis. Eine Integration in die Data Mining Software Clementine über das Forschungszentrum der Daimler-Benz AG in Ulm ist vorgesehen.

Distanzbasierte Klassifikation.

Wenn Informationen über Klassen bereits vorliegen, dann steht meist das Vorhersageproblem im Mittelpunkt des Interesses. Hier konkurrieren vor allem statistische Methoden (z. B. Diskriminanzanalyse), neuronale Netze und Entscheidungsbaumverfahren. Die adaptive distanzbasierte Klassifikation wird bereits seit einem Jahr erfolgreich beim Kredit-Scoring auf der Basis kategorialer (qualitativer) Daten angewendet.

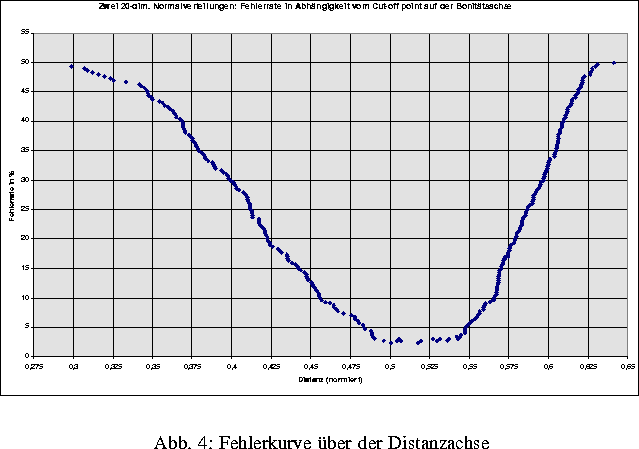
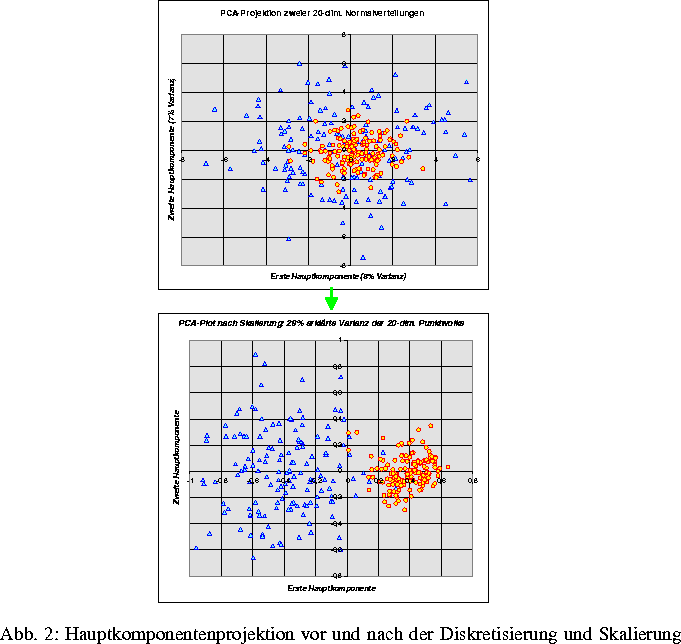
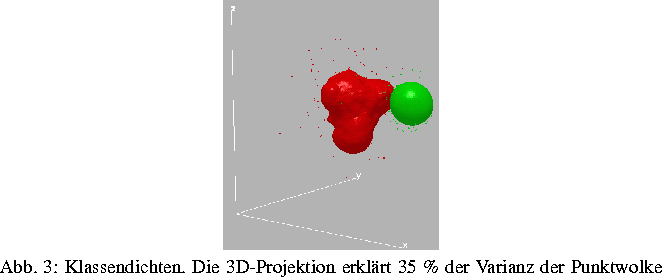
Liegen sowohl qualitative als auch quantitative Informationen über die zu klassifizierenden Objekte vor, dann kann das Modell der distanzbasierten Klassifikation z. B. nach der Diskretisierung der quantitativen Variablen angewendet werden. Ein Beispiel soll die Leistungsfähigkeit dieses Ansatzes graphisch veranschaulichen. Gegeben seien 2 Klassen mit je 150 Objekten im 20-dimensionalen Beobachtungsraum. Die Klasse 1 habe eine Normalverteilung mit dem Erwartungswert 0 und der Kovarianzmatrix I (Einheitsmatrix). Die Erwartungswerte der Klasse 2 seien nur um Wurzel von ein Zwanzigstel von 0 verschieden und die Kovarianzmatrix sei das Vierfache der Einheitsmatrix. Das ist ein bekanntes, schwieriges Klassifikationsproblem. Die Diskretisierung wurde hier durch äquidistante Einteilung in Teilintervalle durchgeführt. Die beiden Bilder der Abb. 2 zeigen die Hauptkomponentenprojektion der zufällig generierten Daten und die Hauptkomponentenprojektion dieser Daten nach erfolgter Diskretisierung und optimaler Skalierung. Abb. 3 gibt auch eine nichtparametrische 3D-Dichteschätzung der Klassen der diskretisierten und skalierten Daten wieder, was insbesondere im Falle großer Datenmengen geeigneter als der Punkteplot in Abb. 2 ist. Schließlich zeigt das letzte Bild die Fehlerkurve des Distanzklassifikators in Abhängigkeit vom Trennpunkt auf der Distanzachse.

Projektliteratur:

1. U. GRIMMER, Clementine: Data Mining Software, in: Classification and Multivariate Graphics: Models, Software and Applications, WIAS-Report No. 10 (1996).
2. H. KAUDERER, H.-J. MUCHA, Supervised Learning with Qualitative and Mixed Attributes. A Local Scaling Approach to Discriminate between Good and Bad Credit Risks, in: Information Systems and Data Analysis, Proc. 21th Annual Conference of the GfKl, Univ. of Potsdam 1997. Series ,,Studies in Classification, Data Analysis, and Knowledge Organization``, (Balderjahn, I., Mathar, R., Schader, M., eds.), Springer-Verlag, in Druck.
3. H.-J. MUCHA, R. SIEGMUND-SCHULTZE, K. DÜBON, Adaptive Cluster Analysis Techniques - Software and Applications, in: Data Science, Classification, and Related Methods, Series ,,Studies in Classification, Data Analysis, and Knowledge Organization``, (Hayashi, C., Ohsumi, N., Yajima, K., Tanaka, Y., Bock, H.-H., Baba, Y., eds.), Springer-Verlag Tokyo (1998), pp. 231-238.