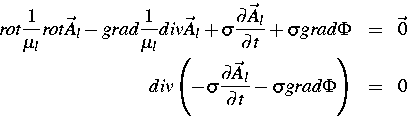Modellierung, Simulation und Optimierung der Oberflächenhärtung von Stahl

 Bearbeiter: J. Fuhrmann (FG 3) , D. Hömberg (FG 1) , M. Uhle (FG 3)  

Kooperation: O. Biro (Technische Universität Graz), J. Sokolowski (Université de Nancy I)

Beschreibung der Forschungsarbeit: Zur Rückbindung der wissenschaftlichen Arbeit an die Praxis wurde verstärkt der Dialog mit der Industrie gesucht. Dazu diente die Präsentation des im letzten Jahr mit Hilfe von Komponenten der pdelib (siehe S. ) entwickelten Solvers für die Simulation des Oberflächenhärtens auf der HANNOVER MESSE. Erstes konkretes Ergebnis ist ein Antrag auf Förderung durch die Stiftung Industrieforschung mit dem Thema ,,Optimierung des Härtens und Umschmelzens mit Laser- und Elektronenstrahl``, an dem zwei Unternehmen aus Sachsen als Pilotunternehmen beteiligt sind.

Die wissenschaftliche Arbeit konzentrierte sich im vergangenen Jahr auf drei Schwerpunkte:

Numerische Simulation der Oberflächenhärtung

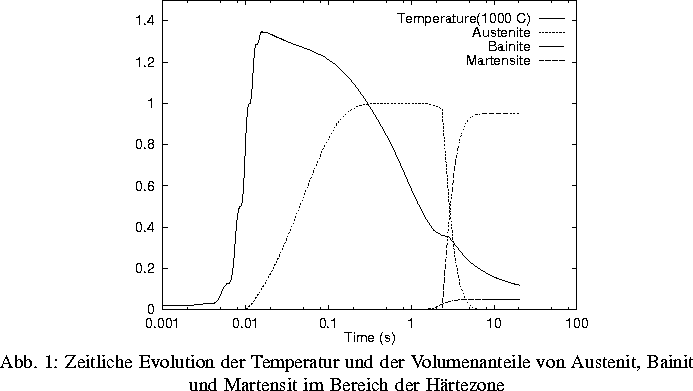
Die Entwicklungsarbeit an dem Programm zur Oberflächenhärtung von Stahl wurde fortgesetzt. Die Beschreibung des zugrundeliegenden Modells sowie umfangreiche Simulationsrechnungen sind in [2] dokumentiert. Die folgende Abbildung zeigt die zeitliche Entwicklung der Temperatur und des Volumenanteils der einzelnen Phasen in einem Punkt im Bereich der Härtezone während einer Laserhärtung mit zusätzlicher Schwingung orthogonal zur Vorschubrichtung.

  

  

Eine Möglichkeit zur Verbreiterung der Härtespur bietet die Oszillation des Laserstrahls orthogonal zur Vorschubrichtung. Abbildung 2 zeigt die Resultate für zwei verschiedene Schwingungsformen mit gleicher Amplitude.

Numerische Verfahren für die 3D-Simulation der induktiven Erwärmung

Die physikalischen Effekte bei der induktiven Wärmebehandlung werden mathematisch durch die Maxwellschen Gleichungen, die Wärmeleitungsgleichung, Materialgleichungen und der Aufgabenstellung angepaßte Rand- und Anfangswerte beschrieben, wobei die zeitliche Ableitung der Verschiebungsstromdichte sowohl im Metall wie auch im umgebenden Gebiet vernachlässigt werden kann. Eine wesentliche Reduzierung der Dimension des Gleichungssystems läßt sich mit der Einführung von vektoriellen und skalaren Potentialen erreichen, wobei die Aufgabenstellung durch zusätzliche Terme für die Coulomb-Eichung und daraus resultierende weitere Randbedingungen zu ergänzen ist [1]. Die numerische Berechnung der elektromagnetischen Felder erfordert im allgemeinen die Lösung von zwei gekoppelten Wirbelstromproblemen (Induktor 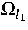$\Omega_{l_1}$, Werkstück $\Omega_{l_2}$ )

$$\begin{eqnarray*} rot \frac{1}{\mu_l} rot \vec{A}_l - grad \frac{1}{\mu_l} div \... ...artial \vec{A}_l}{\partial t} - \sigma grad \Phi \right) & = & 0 \end{eqnarray*}$$

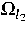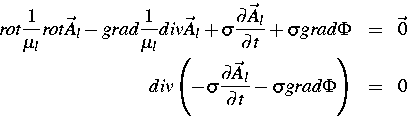
und eines stationären Magnetfeldproblems im nichtleitenden Gebiet $\Omega_{n}$

$$\begin{eqnarray*} rot \frac{1}{\mu_n} rot \vec{A}_n - grad \frac{1}{\mu_n} div \vec{A}_n & = & \vec{0}.\end{eqnarray*}$$

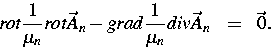
Zur Erreichung hoher Flexibilität bei der Beschreibung von Induktor- und Werkstückgeometrien verwenden wir finite Elemente zur Diskretisierung.

Im Berichtszeitraum wurden Arbeiten zur Modellierung, zur Gittergenerierung und zur Lösung der linearen Gleichungssysteme durchgeführt.

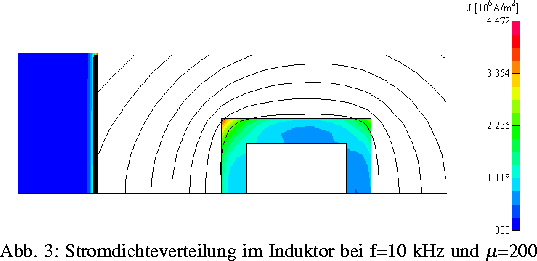
In Zusammenarbeit mit Herrn Dr. Biro (TU Graz) wurden geeignete zweidimensionale Modelle mit dem Programm FEM2D simuliert, um daran die Stromdichteverteilung im Induktor in Abhängigkeit von der Generatorfrequenz und der Permeabilität des Metalls zu studieren. Es zeigte sich dabei, daß bei den in der Praxis auftretenden Mittelfrequenzen und den zu erwartenden Werten für die Permeabilität im Eisen keine Vereinfachungen der Induktormodellierung möglich sind und das Induktorgebiet als Wirbelstromgebiet zu rechnen ist (Abb. 3).

Die numerischen Probleme an Grenzflächen zwischen hochpermeablem Eisen und Luft (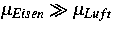$\mu_{Eisen} \gg \mu_{Luft}$) haben ihre Ursache in der Grenzflächenbedingung

$$\begin{eqnarray*} \vec{n}_n \cdot \frac{1}{\mu_n}div \vec{A}_n + \vec{n}_l \cdot \frac{1}{\mu_l}div \vec{A}_l & =& 0\end{eqnarray*}$$

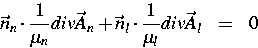
und der Stetigkeit aller Komponenten des Vektorpotentials. Deshalb sollen Kantenelemente zur Ortsdiskretisierung verwendet werden, bei denen nur die Tangentialkomponente des Vektorpotentials stetig ist.

  

Bei den hier auftretenden speziellen Geometrien ist es notwendig, gegebene innere Materialgrenzen exakt widerzuspiegeln. Dafür wurde im Berichtszeitraum das 3D-Gittergenerierungsprogramm T3D auf der Basis paralleler Schichten entwickelt, das die Konstruktion von Gittern mit Delaunay-Eigenschaften gestattet.

Zur Erzeugung einer blocktridiagonalen Matrixstruktur für FEM-Matrizen werden Verfahren zur Reduktion der Bandbreite [3] benutzt. Diese Matrixstruktur läßt sich so in Untersysteme zerlegen, daß Eigenschaften der ursprünglichen Matrix auf diese vererbt werden. Für die entstandene Gleichungssystemstruktur wurde ein Verfahren entwickelt, welches die parallele Lösung von Untersystemen gestattet. Diese Methode soll für die Konstruktion hierarchischer Vorkonditionierer genutzt werden.

Optimierung von Wärmebehandlungen

In [4] wurden notwendige Optimalitätsbedingungen für die optimale Steuerung des Laserhärtens mit punktweisen Zustandsbeschränkungen hergeleitet. Die praktische Umsetzung soll im Rahmen des oben erwähnten Förderungsantrags ,,Optimierung des Härtens und Umschmelzens mit Laser- und Elektronenstrahl`` erfolgen.

Bei den zahlreichen Diskussionen während der HANNOVER MESSE hat sich die Aufgabenstellung, die optimale Form eines Induktors zu finden, als besonders praxisrelevant herausgestellt. Dieses Problem soll in [5] mit Methoden des Optimal Shape Design untersucht werden. Grundlage ist eine Vektorpotentialformulierung der Maxwellschen Gleichungen, gekoppelt mit der Energiebilanz und einer Differentialgleichung für die Evolution des Austenitanteils, der als Maß für die Güte der erreichten Induktorform verwendet wird. Ziel ist es, eine Induktorgeometrie zu finden, die eine gewünschte Austenitverteilung möglichst gut approximiert.

Projektliteratur:

1.   O. BIRO, K. PREIS, On the Use of the Magnetic Vector Potential in the Finite Elemente Analysis of Three-Dimensional Eddy Currents, IEEE Trans. on Magnetics, Vol. 25 (1989), pp. 3145-3159.
2. J. FUHRMANN, D. HÖMBERG, Numerical simulation of surface heat treatments, WIAS-Preprint No. 375 (1997), eingereicht in: Internat. J. Numer. Methods Heat Fluid Flow.
3.   N. E. GIBBS, W. G. POOLE, P. K. STOCKMEYER, An algorithm for reducing the bandwidth and profile of a sparse matrix, SIAM J. Numer. Anal., Vol. 13 (1976), pp. 236-250.
4. D. HÖMBERG, J. Sokoowski, Optimal control of laser hardening, WIAS-Preprint No. 315 (1997), erscheint in: Adv. Math. Sci. Appl.
5. D. HÖMBERG, J. Sokoowski, Optimal shape design of inductor coils for surface hardening, in Vorbereitung.