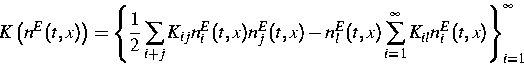Stochastische Modelle und Monte-Carlo-Methoden für Nukleation, Koagulation und Transport von Partikeln in turbulenten Strömungen

Bearbeiter: K. Sabelfeld,  

Kooperation: S. Orszag, (Princeton University, USA), T. Vesala (Helsinki University, Finnland), O. Kurbanmuradov (Turkmenische Akademie der Wissenschaften, Aschchabad), I. A. Shalimova (Russische Akademie der Wissenschaften, Novosibirsk)

Beschreibung der Forschungsarbeit:

Die Untersuchung des turbulenten Transports von reagierenden Wirkstoffen und Brennprozessen stellt eine große theoretische und experimentelle Herausforderung dar (vgl. [12]). Bei der mathematischen Erfassung sind stochastische Modelle von besonderer Bedeutung, da die Wahrscheinlichkeitstheorie eine natürliche Beschreibung von Mischungen und Reaktionen kleiner Partikel in turbulenten Strömungen liefert (vgl. [4] und [1]). Schwerpunkt des Projekts ist die Untersuchung von Nukleation, Transformation und Transport von Aerosol-Partikeln in einer realistischen Umwelt (z. B. turbulente Atmosphäre, Wasser und Boden).

Solche Medien sind charakterisiert durch hohe Fluktuationen der physikalischen Felder. Hierbei ändern sich die zeitlichen und räumlichen Maßstäbe enorm. Dies ist die Ursache aller Schwierigkeiten bei der Benutzung konventioneller deterministischer Methoden, die auf der halbempirischen Gleichung des turbulenten Transports basieren. Deshalb ist die stochastische Betrachtungsweise, die die Natur der Fluktuationen effektiv beschreibt, von besonderem Interesse.

Die untersuchten Prozesse werden durch Randwertprobleme mit stochastischen Parametern für lineare und nichtlineare partielle Differentialgleichungen beschrieben. Es wurden stochastische Modelle benutzt, die sowohl den Itô-Typ stochastischer Differentialgleichungen als auch Systeme von gewöhnlichen Differentialgleichungen mit zufälligen Parametern umfassen (vgl. [6], [3]).

Die stochastischen Algorithmen basieren auf neuen Eulerschen und Lagrangeschen Modellen, die die Bewegung der Partikel in turbulenten und porösen Medien beschreiben und auf probabilistischen Darstellungen der Lösungen der Smoluchowski-Koagulations-Gleichung beruhen (s. [10]).

Die Forschungen zu Aerosol-Formungs-Prozessen erfassen eine Vielfalt von Phänomenen und Anwendungen in Physik, Chemie, Biologie, Medizin und Aerosol-Wissenschaft in der Atmosphäre. Beispiele sind die Berechnung der Nukleationsrate in den Wasser-Säure-Systemen (s. [13]) (ein Schwerpunkt in der Smog-Forschung), Koagulations-Prozesse im Aerosol-Reaktor für die Produktion von Kunststoffen und moderne Aerosol-Technologie für die Landwirtschaft (vgl. [2], [12], [9]). Im Prinzip kann jede Inhomogenität im Gas zu Differenzen in den Geschwindigkeiten der Partikel führen. Dann ist die relative Geschwindigkeit zwischen zwei Partikeln positiv, und es findet eine Kollision und vermutlich Koagulation statt. Folgende Phänomene führen zur Koagulation (s. [12], [9]): Brownsche Bewegung, Gravitationsfall, freie molekulare Kollision, turbulente Bewegung der tragenden Strömung, akkustische Wellen, Gradienten der Dichte, der Konzentration und der Temperatur, elektrische Ladungen und weitere.

Die einfachste inhomogene Form der Smoluchowski-Gleichung ist (s. [10]):

$$\begin{eqnarray*} \frac{\partial n^E(t,x) }{\partial t}+v(t,x)\cdot\nabla_xn^E(t... ...(n^E(t,x)\right)+F(x,t);\ n^E(0,x)=0;\quad x\in R^3;\;t\in[0,T],\end{eqnarray*}$$

wobei $n^E(t,x)=\left\{n^E_i(t,x)\right\}_{i=1}^{\infty}$,

$$K\left(n^E(t,x)\right)=\left\{\frac{1}{2}\sum\limits_{i+j} K... ...um\limits_{i=1}^{\infty}K_{il}n^E_i(t,x)\right\}_{i=1}^{\infty}$$

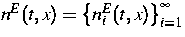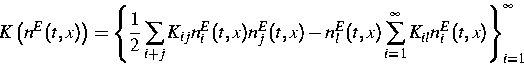
und v(t,x) ein stochastisch simulierender Geschwindigkeitsvektor mit gegebener Verteilung ist. Falls die Koagulation in einer turbulenten Strömung betrachtet wird, ist die Abschätzung der Partikelentwicklung ein sehr schwieriges und auch noch nicht gelöstes Problem. Mathematisch kann man dieses Problem durch Smoluchowski-Gleichungen mit zufälligen Koeffizienten beschreiben (s. [8]).

Folgende Zielstellungen wurden verfolgt:

• Entwicklung neuer stochastischer Algorithmen für die numerische Lösung von partiellen und gewöhnlichen Differentialgleichungen mit zufälligen Parametern. Diese Algorithmen basieren auf neuen lokalen Integralgleichungen (sphärischer Mittelwert) und dem ,,Double Randomization``-Prinzip , s. [7];
• Entwicklung und Analyse stochastischer Methoden für die numerische Simulation der inhomogenen Eulerschen turbulenten Geschwindigkeitsfelder für verschiedene ,,Atmospheric Stratifications``, s. [3];
• Untersuchung neuer Lagrangescher stochastischer Zweipartikelmodelle für voll entwickelte Turbulenz, s. [3];
• Anwendung Eulerscher und Lagrangescher stochastischer Modelle zur Simulation des Transports von Aerosolpartikeln in turbulenter Atmosphäre (vgl. [6], [3]);
• Aufbau und Untersuchung stochastischer Algorithmen für die Lösung der inhomogenen Smoluchowski-Gleichungen mit Anwendungen in der Numerik der Nukleation und Koagulation von Partikeln verschiedener Werkstoffe (vgl. [8], [11], [13]).

Projektliteratur:

1.   U. FRISCH, Turbulence, Cambridge University Press, 1996.
2.   K. P. KOUTZENOGII, A. I. LEVYKIN, K. K. SABELFELD, Numerical simulation of the kinetics of aerosol formation in the free molecular collision regime, Journal of Aerosol Science, 27 (1996), No. 5, pp. 665-679.
3.   O. KURBANMURADOV, K. K. SABELFELD, D. KOLUHIN, Stochastic Lagrangian models for two-particle motion in turbulent flows. Numerical results, Monte Carlo Methods and Appl., 3 (1997), No. 3, pp. 199-223.
4.   A. S. MONIN, A. M. YAGLOM, Statistical Fluid Mechanics, M. I. T. Press, Cambridge, 2 (1975).
5.  K. K. SABELFELD, Monte Carlo Methods in Boundary Value Problems, Springer Verlag, Berlin (1991), p. 283.
6.   K. K. SABELFELD, O. KURBANMURADOV, Stochastic Lagrangian models for two-particle motion in turbulent flows, Monte Carlo Methods and Appl., 3 (1997), No. 1, pp. 53-72.
7.   K. K. SABELFELD, I. A. SHALIMOVA, Spherical Means for PDEs, VSP, Utrecht, The Netherlands, 1997.
8.   K. K. SABELFELD, A. A. KOLODKO, Monte Carlo simulation of the coagulation processes governed by Smoluchovsky equation with random coefficients, Monte Carlo Methods and Appl., 3 (1997), No. 4, pp. 275-310.
9.   P. SAFFMAN, J. S. TURNER, On the collision of drops in turbulent clouds, J. Fluid Mech., 1 (1956), pp. 16-30.
10.   M. SMOLUCHOWSKI, Drei Vorträge über Diffusion, Brownsche Bewegung und Koagulation von Kolloidteilchen, Phys. Z., 17 (1916), pp. 557-585.
11.   A. A. KOLODKO, W. WAGNER, Convergence of a Nanbu type method for the Smoluchowski equation, Monte Carlo Methods and Appl., 3 (1997), No. 4.
12.   M. M. R. WILLIAMS, S. K. LOYALKA, Aerosol Science. Theory and Practice, Pergamon, New York, 1991.
13.   E. L. ZAPADINSKY, K. K. SABELFELD, M. KULMALA, D. M. RAKIMGULOVA, Heterogeneous nucleation in non-uniform media: numeriacal simulation, J. of Aerosol Science, 26 (1996), No. 8, pp. 1189-1195.